CHORD M-Scaler Review (Upsampler)

[bearcatsandor]

Ahhh yes, Yoko Kanno,

Especially the music from Cowboy Bebop is brilliant, but she made music for a lot of Anime.

She's made a few. I have 64 of her albums. She's by far my favorite artist.

 

[Nutul]

I have 64 of her albums.

OMG

 

[AdrianusG]

She's made a few. I have 64 of her albums. She's by far my favorite artist.

Wow,

I guess she must be i you have that many albums, any titles you can recommend (except cowboy bebop, which i already have!) I like jazz ; fusion ; rock and mixes there-off, also funk and blues.

 

[AdrianusG]

Wow,

I guess she must be i you have that many albums, any titles you can recommend (except cowboy bebop, which i already have!) I like jazz ; fusion ; rock and mixes there-off, also funk and blues.

must be "If you have that many albums" of course ....Typo

 

[staticV3]

must be "If you have that many albums" of course ....Typo

You can edit your posts to fix typos. No need to make an extra post to correct them

Edit: see here

 

[bearcatsandor]

Wow,

I guess she must be i you have that many albums, any titles you can recommend (except cowboy bebop, which i already have!) I like jazz ; fusion ; rock and mixes there-off, also funk and blues.

Send me a DM, so that we don't derail this crazy [train] thread. I'm always happy to recommend my favorites.

 

[Neric]

There's 104 pages... maybe somewhere this is brought up but I found it hilarious:

From sterophile review (which ends up being positive, but what isn't at that magazine)

Digital filters and upsampling
In the promotional literature for the M Scaler, Chord writes, "The Hugo M Scaler . . . takes the digital file and repairs it, adding back the information lost between the samples, then it sends the repaired file to the DAC. . . . With 705,600 samples per second, a huge amount of important information that was lost when creating the 44.1 digital file is now recovered. The more samples, the closer you get to the original analog signal. . . . The Hugo M Scaler in essence places 15 additional new musical samples in between each original musical sample, resulting in an astounding improvement in the recreation of the original music signal."

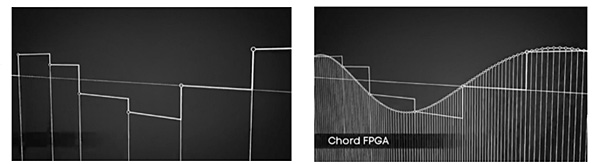
My eyebrows raised, I kept reading. Referring to the figure reprinted here, the text states that "The Hugo M Scaler takes a rough stairstep CD quality waveform and transforms it into a smooth analog-like waveform. That quantum leap in sampling brings a breathtaking leap in detail, accuracy and realism to your music."

Hmm. The measurements I performed to accompany our reviews of the dCS 972 and Purcell definitively showed that upsampling doesn't add information above the Nyquist frequency—22.05kHz with CD data—of the lower sample rate. So what is the M Scaler doing?

In one of the first articles I wrote for Stereophile, "Zen & The Art of D/A Conversion," which was published in September 1986, I discussed how the recovered analog signal is not directly described by the levels of the digital samples. Instead, the interaction between those samples and the impulse response of a digital low-pass reconstruction filter recreates the analog waveform—not just at the sampling intervals but between them (footnote 3). By processing the incoming data with a low-pass filter featuring an extremely long impulse response, the M Scaler makes it possible for the accompanying DAC to more accurately reconstruct the analog signal. In effect, it replaces the DAC's digital filter with its own, as the DAC's filter is now operating at the higher sample rate, and its cutoff is one or more octaves above the original data's Nyquist frequency.

Sounds like snake oil that fatens the company's bottom line and the sales guys pocket.

 

[voodooless]

Sounds like snake oil that fatens the company's bottom line and the sales guys pocket.

It’s not just snake oil, it’s also lies…. And staircases

 

[DonR]

There's 104 pages... maybe somewhere this is brought up but I found it hilarious:

From sterophile review (which ends up being positive, but what isn't at that magazine)

Sounds like snake oil that fatens the company's bottom line and the sales guys pocket.

It is able to do that because it has knowledge of every piece of recorded music, past, present and future, and was there when the recording was made so it knows all the "information lost between the samples".

 

[Neric]

It is able to do that because it has knowledge of every piece of recorded music, past, present and future, and was there when the recording was made so it knows all the "information lost between the samples".

And because they frame the lie that there's "missing data"

There are pictures of the inside - no way is there enough chips to hold all the data

 

[DonR]

And because they frame the lie that there's "missing data"

There are pictures of the inside - no way is there enough chips to hold all the data

It has a quantum entangled connection to every musician in the world. That is the only "feasible" explanation. Occam's Razor and all that, you know.

 

[antcollinet]

It’s not just snake oil, it’s also lies…. And staircases

Stair cases are lies.

 

[Ken Tajalli]

Stair cases are lies.

No silly!
he means its snakes'n'ladders.

Snakes and ladders - Wikipedia

en.m.wikipedia.org

 

[AdrianusG]

Poll - The most useless thing ever

1) This subtitle

2) Diet water

3) Chord M-scaler

Do I really really have to choose?

there's no 4) All of the above?

 

[AdrianusG]

Do I really really have to choose?

there's no 4) All of the above?

Although 2) Diet Water makes me laugh the most.

 

[voodooless]

Stair cases are lies.

Sure, it one on the grand audiophile conspiracies. Staircases are the flat earth of high fidelity. “They” want you to think that they don’t exist, yet you can clearly see them in all those pictures!

 

[Leporello]

In my own personal case, oversampling to DSD 256 and 512, using HQPlayer (gauss filters, EC modulators), into a simple DSC-2 style DAC with no onboard processing, results in the best digital sound I have ever heard.

Time for a reliable listening test.

 

[HarmonicTHD]

Time for a reliable listening test.

Remember he is here to teach us „know it all“ a lesson.

 

[SIY]

OK, I have not read all of this thread, but most of it seems like a bunch of "know it alls" espousing their greater understanding of digital audio than Rob Watts', uhhh, sure you do!
At least Amir himself appears to exhibit some knowledge of digital audio and filtering. If you really think that the oversampling/filtering incorporated into an ESS DAC chip is already, the best it could possibly be, either you are deaf, or have not actually taken the opportunity to listen to better.
I do not own an Mscaler, and neither do I ever intend to, but I do own HQPlayer, and a good server (I9-9900K) to take advantage of HQPlayer's vast options for oversampling/filtering.

There are two possible reasons to oversample outside of the DAC itself:

1. To apply better, more precise digital filters than are possible to incorporate into a limited processing power DAC chip.

or:

2. ( often better) to be able to use a very simple NOS DAC without the inherent limitations of actually converting to analog without oversampling.

Whether or not these approaches actually lead to better sonic performance is for the listener to decide for themselves, and not to be determined by "know it alls" who clearly do not...

In my own personal case, oversampling to DSD 256 and 512, using HQPlayer (gauss filters, EC modulators), into a simple DSC-2 style DAC with no onboard processing, results in the best digital sound I have ever heard. A Topping D-90 sounds broken by comparison. The one DAC I have heard which can compare without external oversampling is the Mola Mola Tambaqui, note is uses a similar approach, with a lot of onboard processing power (3 powerful DSP chips), oversampling to a very high rate single bit signal, and then converting via a discrete 32 element FIR filter.

Before you jump to conclusions, you should listen for yourself. To imagine that an ESS 9028, or similar single piece of silicon can do as good a job as an I9-9900K plus simple discrete DAC conversion stage is silly, the ESS chip is limited by its size and power, and also, likely by the fact that its digital processing is shared in very close proximity to analog signals. If you own a D-90, take it to dealer to compare in a really good system vs a Tambaqui, see what you think, before just taking someone's word for it.

I’m trying to find something worthwhile in this wall of words but have failed. Get back to us when you have actual evidence of any sonic differences.

 

[DSJR]

Apparently, there's a new M-Scaler coming and maybe a top model dac as well. Head of Chord says the former takes the Dave into a higher (again) realm or words to that effect. I read this on Pink Fish Media while making way to the Bristol Show report, a forum I used to post extensively on when in the wildnerness until ten or more years back and the posters there now DO NOT like ASR and the sinad chasers of Chinese made gear it seems. I used to post there all the time, but there's no arguing with people who've never knowingly had their senses fooled as I/we have... Most of the fervour is Rega continuing their move up-market (Oh Gawd) and English Audio making re-imagined Leak valve amps by the loos of things (originals fetch silly money but are funky, charming sounding curiosities at best by today's standards just as my rebuilt quad II's are charmingly listenable but hardly 'high fidelity' really).

I still maintain a Chord pre-power combination at any price isn't going to get the best subjectively out of a Dave, but it needs someone else to possibly confirm or deny plus proper testing (yes @SIY I do understand, but it ain't gonna happen here I suspect unless Amir has things sent to him).