Claim
A claim is frequently made that DAC digital filters with a lot of taps can make a significant difference in sound quality. Some software packages and even hardware manufacturers are touting the benefits of large FIR filters, often with millions of taps, supposedly because these produce a more natural, smoother, analog sound or improve "time domain" accuracy, whatever that means. Some of these are sold at large premiums, supposedly because of the complexity of implementing large filters.
Test
Let's use DeltaWave software to find out the real story. I'll use a null test to produce a difference between a music file generated with two different size filters, and then measure the differences in frequency and time domain. For audibility testing, we'll also listen to it. Let's see if there's something to these claims!
The music file I'll be using is one some you may recognize as one used in other null tests on another forum:
http://www.mediafire.com/file/5hg6wl6ygql7217/Original2.wav/file
Since DeltaWave can generate and apply various size FIR filters, from 1k to 16M (yes, 16 million) taps, I decided to compare a 16k filter to a 4M one.
The Original2.wav music file is 24/44.1k, about 2 minutes. I'll place both filters with a cutoff at 21,150Hz. A shorter filter will have a gentler slope than the 4M one. The 4M one is a brickwall filter, as it drops the signal by nearly 300dB within a 20Hz transition band.
Applying FIR filters is just a simple setting in DeltaWave, so I used each filter on the original music file, and then saved the results as 64-bit floating point WAV. I then loaded these up in DeltaWave to compute the difference. Below are the results.
Results
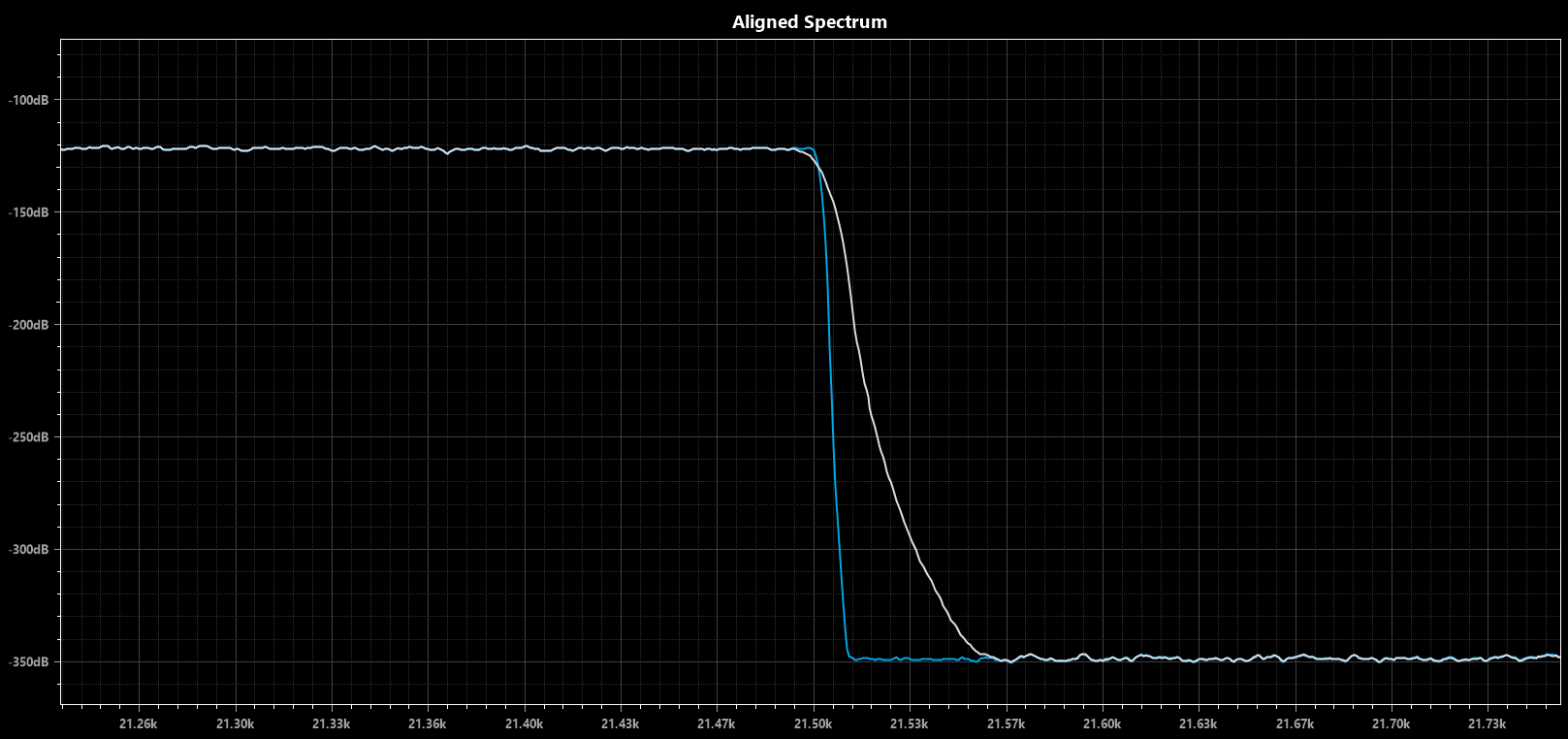
First, the spectrum comparison. The only difference is visible right around the transition band (white line is obviously the 16k filter, blue is the 4M taps filter). I zoomed in on that area to show it better:
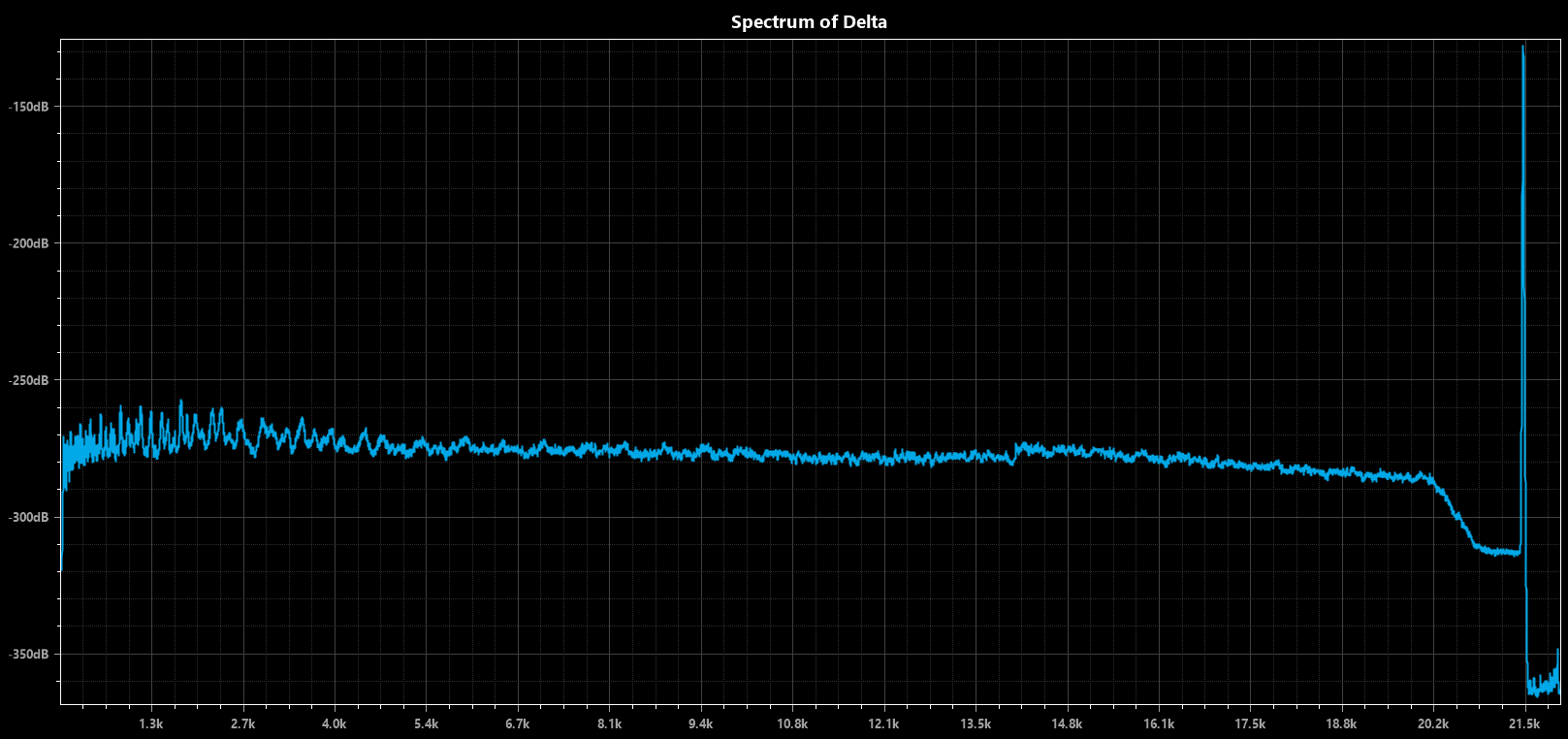
Spectrum of the difference file (null file) generated by subtracting the two filtered files... not much difference here, except past the cutoff where we already know the two filters are different:
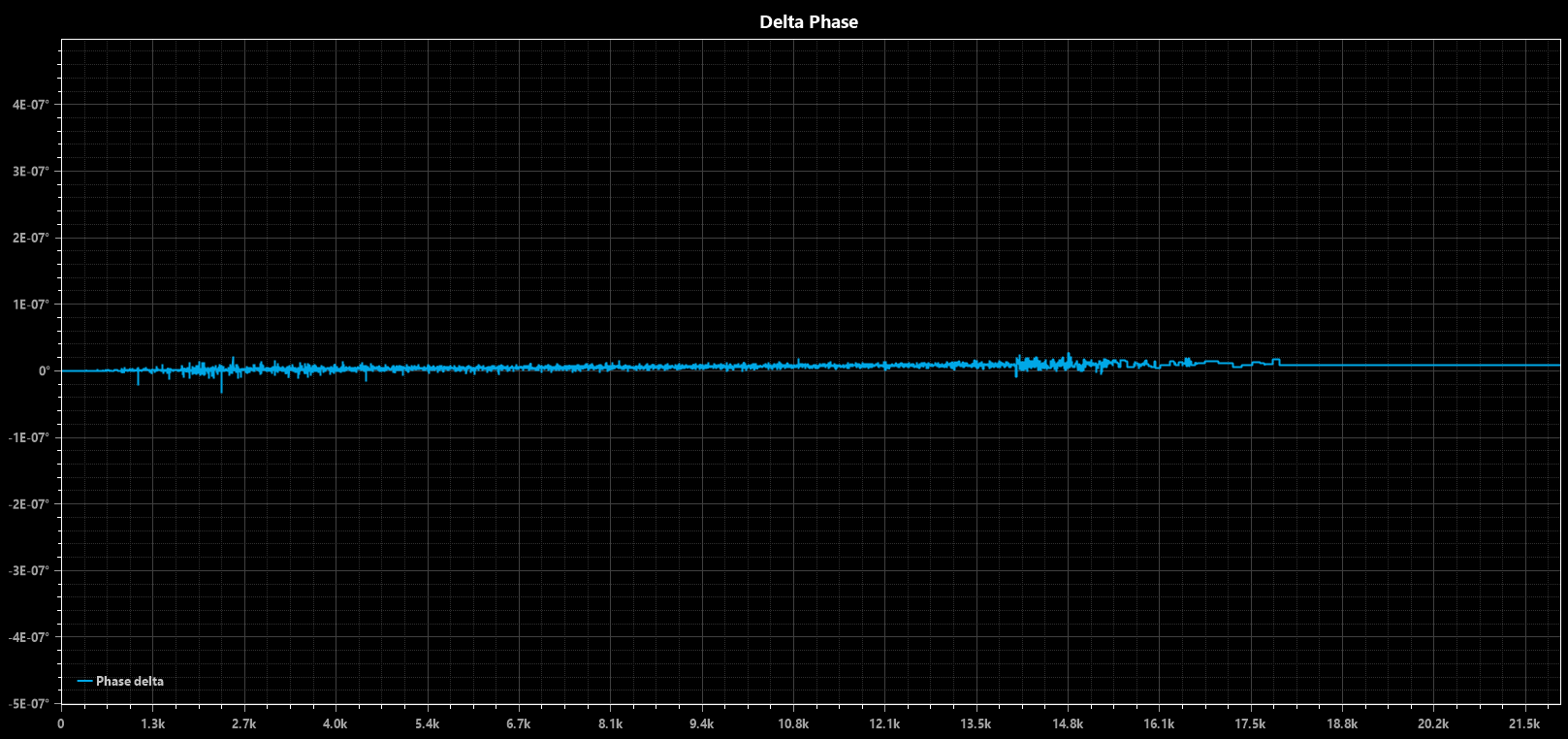
Here's the phase difference between the two files (indicative of timing differences or group delay).
Note the scale on the left is 1x10^-7 degrees (0.0000001)! Nothing to see here... as one would expect with a linear FIR filter:
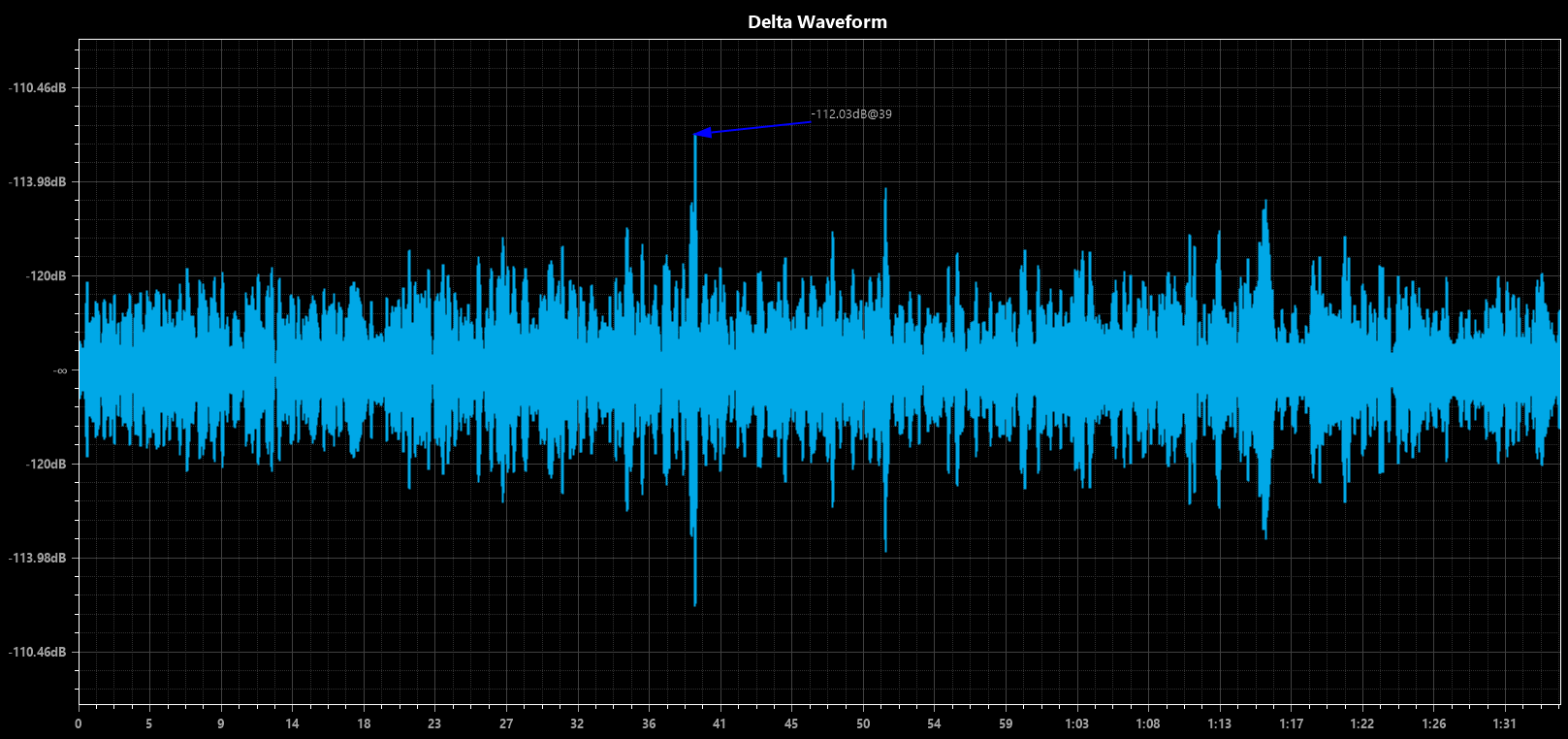
Let's check out the time-domain differences. Below is the actual waveform plot of the null file. Except for some sharp transients that have frequencies that extend past the filter cutoff, everything else is below -120dB! And even the sharp transients don't exceed -112dB, so way below audibility, considering that they are above 21kHz:
Here's the RMS average of the entire null file in time domain. Note that it's -229dBA, and -124.44dBFS. In other words, way below any thresholds of audibility, A-weighted or not:

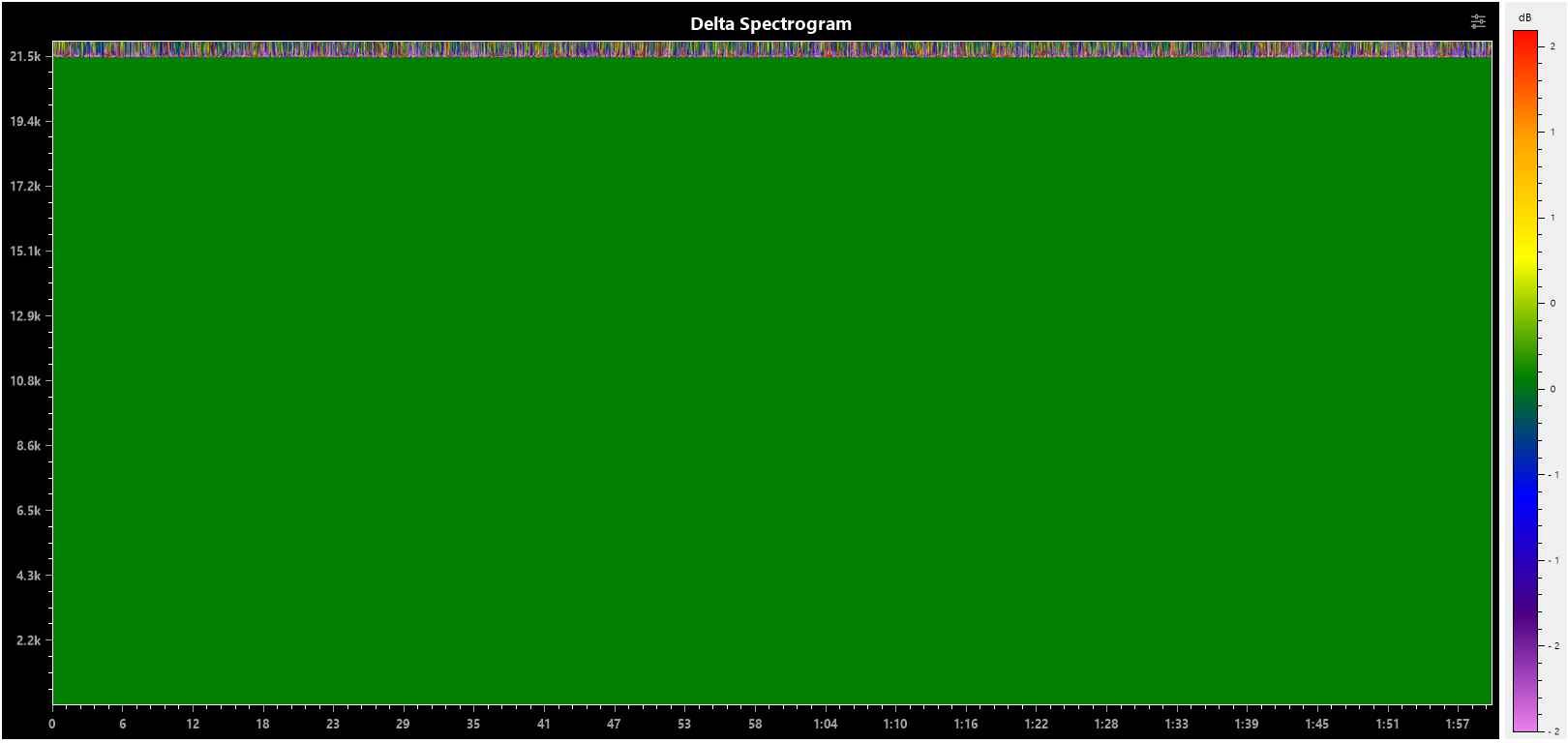
Let's take a look at the difference spectrogram, maybe something will become apparent there... No difference at all except above the filter cutoff frequency:
And finally, here's the actual difference file: https://app.box.com/s/dde7ua0x668ismhebxpzxr57gh33u0jn
The file is a 32-bit FP WAV, mono to save space/size, about a 39MB download. Feel free to listen to see what the differences sound like between a 16k and 4M-size FIR filters. Personally, I can't hear anything even after raising the level by a whopping 100dB!
Conclusion
There's no audible benefit to all those heroic extra taps in a 4M-sized FIR filter. Don't believe me? Listen for yourself.
A claim is frequently made that DAC digital filters with a lot of taps can make a significant difference in sound quality. Some software packages and even hardware manufacturers are touting the benefits of large FIR filters, often with millions of taps, supposedly because these produce a more natural, smoother, analog sound or improve "time domain" accuracy, whatever that means. Some of these are sold at large premiums, supposedly because of the complexity of implementing large filters.
Test
Let's use DeltaWave software to find out the real story. I'll use a null test to produce a difference between a music file generated with two different size filters, and then measure the differences in frequency and time domain. For audibility testing, we'll also listen to it. Let's see if there's something to these claims!
The music file I'll be using is one some you may recognize as one used in other null tests on another forum:
http://www.mediafire.com/file/5hg6wl6ygql7217/Original2.wav/file
Since DeltaWave can generate and apply various size FIR filters, from 1k to 16M (yes, 16 million) taps, I decided to compare a 16k filter to a 4M one.
The Original2.wav music file is 24/44.1k, about 2 minutes. I'll place both filters with a cutoff at 21,150Hz. A shorter filter will have a gentler slope than the 4M one. The 4M one is a brickwall filter, as it drops the signal by nearly 300dB within a 20Hz transition band.
Applying FIR filters is just a simple setting in DeltaWave, so I used each filter on the original music file, and then saved the results as 64-bit floating point WAV. I then loaded these up in DeltaWave to compute the difference. Below are the results.
Results
First, the spectrum comparison. The only difference is visible right around the transition band (white line is obviously the 16k filter, blue is the 4M taps filter). I zoomed in on that area to show it better:
Spectrum of the difference file (null file) generated by subtracting the two filtered files... not much difference here, except past the cutoff where we already know the two filters are different:
Here's the phase difference between the two files (indicative of timing differences or group delay).
Note the scale on the left is 1x10^-7 degrees (0.0000001)! Nothing to see here... as one would expect with a linear FIR filter:
Let's check out the time-domain differences. Below is the actual waveform plot of the null file. Except for some sharp transients that have frequencies that extend past the filter cutoff, everything else is below -120dB! And even the sharp transients don't exceed -112dB, so way below audibility, considering that they are above 21kHz:
Here's the RMS average of the entire null file in time domain. Note that it's -229dBA, and -124.44dBFS. In other words, way below any thresholds of audibility, A-weighted or not:
Let's take a look at the difference spectrogram, maybe something will become apparent there... No difference at all except above the filter cutoff frequency:
And finally, here's the actual difference file: https://app.box.com/s/dde7ua0x668ismhebxpzxr57gh33u0jn
The file is a 32-bit FP WAV, mono to save space/size, about a 39MB download. Feel free to listen to see what the differences sound like between a 16k and 4M-size FIR filters. Personally, I can't hear anything even after raising the level by a whopping 100dB!
Conclusion
There's no audible benefit to all those heroic extra taps in a 4M-sized FIR filter. Don't believe me? Listen for yourself.

