Crossover filter - Effects on the vertical radiation

[ctrl]

What is usually neglected in many considerations of crossover filters are the effects on vertical radiation.
Since most loudspeaker designs, apart from coaxial designs, use vertically offset sound sources, a typical case will be examined here.

I did not want to use point sources, but still wanted to provide the best possible sound addition at the crossover frequency.
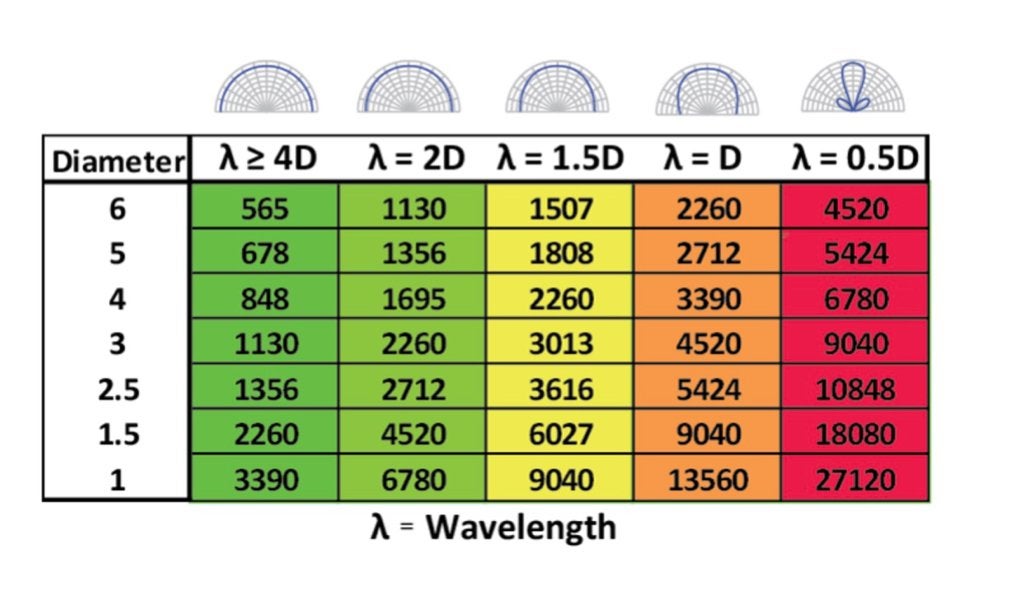
As a compromise I chose a 34mm dome and a 4 inch flat membrane driver placed 0.13m apart (a realistic distance) on an infinite baffle (therefore there is only frequency responses of +-90°). The crossover frequency in the examples is always 2kHz.

The sound sources are closer together ( 0.13m) than the wavelength at the crossover frequency 2kHz -> 0.17m, which is generally considered the rule of thumb for a "good" crossover.
The outermost frequency ranges were realistically limited to 20Hz and 20kHz by filters to show that even with the best possible frequency range of the driver, there are still small errors due to phase shifts of the drivers.

Many people are probably not really aware of what the vertical dispersion behavior of a loudspeaker with an optimally implemented crossover filter should look like and wonder about large sound pressure level drops (in the vertical plane) around the crossover frequency, may even think that the crossover has not been implemented correctly, because of the severe cancellations.

About the influence of the crossover filter on the sound power of the speaker, there are very informative articles. Therefore, it will be discussed here only in passing. One should only realize that practically nobody listens to his loudspeakers in a perfect diffuse field and horizontal listening influences are evaluated differently than vertical ones.

The diagrams always have the following order:
1. FR, Power & DI and Polar diagram
2. vertical FR above reference axis
3. vertical spectrogram

Note: For the vertical FR and spectrograms, all negative angles point above the reference axis.
I did not have the mood to correct this - sorry, I know I'm a bitch


The following applies to all "Power&DI" frequency response curves:

Let's start with the crossover, which is hardly feasible and yet considered by many audiophiles as the only true one.

Butterworth first order (BU1)
A crossover that is asymmetrical in the vertical direction with a beam angle of -15° (with same-pole connection).
Note that negative angles point up, so the polar diagram looks "wrong".



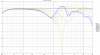
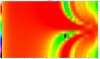
Butterworth third order (BU3)
Before LR filters became known, this was a very common filter. For the lowest group delay, the drivers are connected with reverse polarity, resulting in a -15° tilted radiation pattern (Note that negative angles point up, so the polar diagram looks "wrong").
Because of the constant sound power around the crossover frequency, this filter is preferred by some to LR filters.



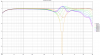
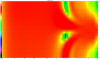
Linkwitz-Riley second order (LR2)
Used more often in the crossover of woofer and midrange. Rather rarely in the crossover to the tweeter.



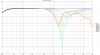
Linkwitz-Riley forth order (LR4)
The "standard" among the crossover filters.



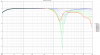
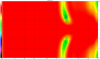
Linkwitz-Riley eighth order (LR8)
By using DSP in active loudspeaker projects, very steep filter slopes are no longer a problem - if you are willing to accept a large group delay (at normal crossover frequency) - or use FIR.




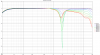
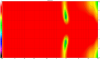
Note: In the attachment you can find the whole VCAD project. With it you can try out different filters yourself - even exotic ones like a Harsch crossover.
There you can also study the phase relationships and the effect on the group delay.

 

[Tom Danley]

Fwiw, if you can get two drivers to be less than 1/4 wl apart where they interact, they add coherently without cancellation notches and lobes.
It does take an alternative crossover shape to combine without the normal "all pass" phase shift but it is possible.
Tom

 

[ctrl]

Pay attention to the vertical frequency responses that arrive at the listening position as first order ceiling reflections - i.e. 40, 50 60 degrees (in my examples the negative angles).

The difference between, for example, BU3 and LR4 is striking and and many perceive these crossovers as very different - although the horizontal radiation of both would be almost identical.

As a possible explanation for the different (spatial) sound impressions of BU3 and LR4 crossover, one could take the directional bands of Blauert ("Blauertsche Bänder").
The BU3 crossover would emphasize the 0° band around 3kHz and make the reproduction more "present", "move further forward".

Source: Spatial Perception

 

[ctrl]

Fwiw, if you can get two drivers to be less than 1/4 wl apart where they interact, they add coherently without cancellation notches and lobes.
It does take an alternative crossover shape to combine without the normal "all pass" phase shift but it is possible.

I would be happy if you would show this with the attached VCAD project.

At a 1/4 wavelength distance, which would be about 660Hz in the VCAD project, a crossover with LR4 does not make a bad impression:

 

[headshake]

The sound sources are closer together ( 0.13m) than the wavelength at the crossover frequency 2kHz -> 0.17m, which is generally considered the rule of thumb for a "good" crossover.

Doesn't the hump in the DI go away if you increase the distance to greater than the wavelength of the XO? Kimmo promoted a 1.2x the WL of the XO spacing.

 

[ctrl]

Doesn't the hump in the DI go away if you increase the distance to greater than the wavelength of the XO? Kimmo promoted a 1.2x the WL of the XO spacing.

To which crossover filters does your statement refer? A BU3 does not show a DI hump in the range of the crossover frequency and the DI hump when using LR4 does not go away at a crossover frequency of 2.2kHz (1.2 * WL of driver distance).

You can also test it yourself with the VCAD project file if I misunderstood your question.

 

[hardisj]

The sound sources are closer together ( 0.13m) than the wavelength at the crossover frequency 2kHz -> 0.17m, which is generally considered the rule of thumb for a "good" crossover.

Good thread. Just wanted to add this...

FWIW, the rule of thumb I've always followed is 1/2 wavelength. At 2kHz that is about 3.38 inches (0.08m). Tough to do when talking CTC between a 6-inch midwoofer and a 1-inch dome tweeter but it is manageable. This is why when I see a speaker where a basket is cut to push the two drivers' CTC together, I immediately assume the company knows what they are doing. Otherwise, why spend the money to cut baskets or have custom molds when off-the-shelf parts will do.

Also, the graphic below provides a good illustration of the (significant, IMHO) difference when using the full-wavelength rule vs the half-wavelength rule. (Note: D= Diameter, in inches)

 

[Tom Danley]

Good thread. Just wanted to add this...

FWIW, the rule of thumb I've always followed is 1/2 wavelength. At 2kHz that is about 3.38 inches (0.08m). Tough to do when talking CTC between a 6-inch midwoofer and a 1-inch dome tweeter but it is manageable. This is why when I see a speaker where a basket is cut to push the two drivers' CTC together, I immediately assume the company knows what they are doing. Otherwise, why spend the money to cut baskets or have custom molds when off-the-shelf parts will do.

View attachment 128863






Also, the graphic below provides a good illustration of the (significant, IMHO) difference when using the full-wavelength rule vs the half-wavelength rule. (Note: D= Diameter, in inches)

Actually, a 1/2 wl separation produces a forward lobe, the trick with crossovers is controlling what direction it is. If you want two sources to add into one new source (like if you close couple two subwoofers) they need to be not more than 1/4 wl apart. It's hard to do this so few do.
Here is the radiation pattern two sources produce given the spacing vs wl

https://www.falstad.com/interference/

Or if talking about at subwoofer frequencies, but the issue is frequency independent.

https://forums.prosoundweb.com/index.php?action=dlattach;topic=157886.0;attach=15954;image
Tom

 

[Tom Danley]

I would be happy if you would show this with the attached VCAD project.

At a 1/4 wavelength distance, which would be about 660Hz in the VCAD project, a crossover with LR4 does not make a bad impression:
View attachment 128827

Hi
I am not familiar with that program so can't offer much help with that.

I would offer that the named variety of crossovers assume the drivers are in the same point in time and if done by the book, produce a 90 degree phase shift per order from high to low (also called all pass phase shift).
Normally the drivers also radiate from two points in space / not close enough together to add coherently into one new source unilaterally and so the trick is dealing with the lobes and nulls from the interference pattern.

I should have explained too that if you do put the drivers a 1/4wl or less apart, they will have a gain from mutual coupling and your crossover will have to account for that apparent gain at crossover.
Fwiw, a really powerful program for active or passive crossovers is LSPcad. It allows one to set a target and fit the curve, allows for passive values to be variables etc.

I have screen shots of two loudspeakers handy which exhibit no apparent crossover phase shift. One is a KEF speaker I had at work. The other is an old Synergy horn i built in 2006 and measured in my living room in 2014 when i was playing with FIR filters.

The part about drivers adding coherently if close enough applies inside a horn as well, this cabinet has 7 horn loaded drivers but appears to be a single driver and not a 3 way horn. The "Not FIR" response is the passive crossover.
So are you building a speaker now, it sounds like it. If so what do you use to take measurements?
Best
Tom

 

[Razorhelm]

The wharfedale diamond 9.1 has the cut basket to get the tweeter closer together
And it measures very well off axis

About 6mins in he talks about this.

 

[hardisj]

Actually, a 1/2 wl separation produces a forward lobe, the trick with crossovers is controlling what direction it is. If you want two sources to add into one new source (like if you close couple two subwoofers) they need to be not more than 1/4 wl apart. It's hard to do this so few do.
Here is the radiation pattern two sources produce given the spacing vs wl

https://www.falstad.com/interference/

Or if talking about at subwoofer frequencies, but the issue is frequency independent.

https://forums.prosoundweb.com/index.php?action=dlattach;topic=157886.0;attach=15954;image
Tom

Understood. But, as you indicated, a 1/4 wave separation isn’t really feasible for most standard designs. Well, I suppose any standard design, really.

Tom, I just want to take the opportunity to welcome you to the site. I’ve been a long time follower of your synergy horns. Really fascinating stuff. I hope one day to be able to hear (or maybe even test) them.

Erin

 

[Zvu]

Doesn't the hump in the DI go away if you increase the distance to greater than the wavelength of the XO? Kimmo promoted a 1.2x the WL of the XO spacing.

To be precise, Kimmo Saunisto proposed next equation:

c-c = 1.2 * 344000 / XOf

c-c : center to center distance in mm
1.2 : coefficient
344000 : speed of sound in air expressed in mm/s
XOf : crossover frequency in Hz

 

[headshake]

To which crossover filters does your statement refer? A BU3 does not show a DI hump in the range of the crossover frequency and the DI hump when using LR4 does not go away at a crossover frequency of 2.2kHz (1.2 * WL of driver distance).

You can also test it yourself with the VCAD project file if I misunderstood your question.

Thanks for the sims btw.

The LR4 and LR8 are what I was talking about. If I set the y-axis -115mm for the woofer in your vcad sim, the nulls are moved way off-axis and DI is smooth.

Am I breaking the sim or is it a matter of setting the c-to-c spacing to the XO you want to use if you want the nulls way off-axis?

 

[richard12511]

Understood. But, as you indicated, a 1/4 wave separation isn’t really feasible for most standard designs. Well, I suppose any standard design, really.

Tom, I just want to take the opportunity to welcome you to the site. I’ve been a long time follower of your synergy horns. Really fascinating stuff. I hope one day to be able to hear (or maybe even test) them.

Erin

The SH50 is to this day the best imaging speaker I've ever heard, and I heard it blind. I've got Genelec 8351b, which are just about perfect, and they do some things better, but I wish they imaged as well as that synergy horn did.

 

[ctrl]

I am not familiar with that program so can't offer much help with that.

No problem, if you specify the crossover filters for tweeter and woofer of the "2-way speaker in infinite baffle" to get the

alternative crossover shape to combine without the normal "all pass" phase shift

I can adjust the simu accordingly and show it here in the thread.

I would offer that the named variety of crossovers assume the drivers are in the same point in time and if done by the book, produce a 90 degree phase shift per order from high to low (also called all pass phase shift).
Normally the drivers also radiate from two points in space / not close enough together to add coherently into one new source unilaterally and so the trick is dealing with the lobes and nulls from the interference pattern.

Yep, that's exactly what the examples are meant to show.

Everyone can try what happens when the woofer is offset in the z-axis.
Crossover filters with constant sound power (BU1, BU3) provide anything but "constant" or "equal" first order reflections from floor and ceiling (because of asymmetric lobing)...

The LR4 and LR8 are what I was talking about. If I set the y-axis -115mm for the woofer in your vcad sim, the nulls are moved way off-axis and DI is smooth.
Am I breaking the sim or is it a matter of setting the c-to-c spacing to the XO you want to use if you want the nulls way off-axis?

Yep, you're kind of breaking the simulation. If you use -130mm the result will be even better.

I don't know how Kimmo calculates the y-axis phase shift in VCAD, my explanation for your result would be:
Since in my example the positive and negative angles are reversed, for VCAD the speaker is upside down (woofer is above the tweeter).
If you now set -130mm for the y-axis of the woofer, it shifts it downwards so that it is exactly on top of the tweeter - you have virtually created a coax, with all the positive consequences for vertical dispersion.

 

[fluid]

Kimmo expanded on some of his ideas in the Vituix thread on diyaudio before he moved to HTG.

1) Tweeter (wave guide) much less directive at XO than woofer.
2) c-c distance ca. 1.2 x wave length at XO.
3) Box shape to decrease directivity at XO and increase directivity octave above XO (smoothly with diffraction without sharp edges).
4) Phase match octave above XO and possibly clear mismatch octave below XO.

Items 1-3 are implemented in proper 2-way design. This is very rare in practice in my opinion.


This post copied below gives a better explanation of his reasoning and why going as close a practical may not give the best end result (in a 2 way) unless you can go coaxial or Multiple Entry Horn to reduce it to below 1/4 wavelength.

"Quote:
Originally Posted by DaveFred
1) Waveguides are good, they make the tweeter less directive at XO than the woofer."

Possibly but not necessarily. Wave guide is quite large - possibly too large in many modern speakers though large wave guide might be needed with shoe box enclosure. Equal directivity at XO causes hump to directivity index without significant (~90 deg) phase mismatch.

"Quote:
Originally Posted by DaveFred
2) Usually I try to make the tweeter and woofer as close together as possible. Are you saying there is a specific formula for spacing? And that maybe closer isn't always better?
"c-c distance ca. 1.2 x wave length at XO."
Could you expand on this?"

'As close as possible' could be 'the worst possible' for directivity index i.e. either on axis (~listening window) or power response or both should be compromised to get balanced sound.
Of course if minimal vertical lobing is priority #1 then you should locate as close as possible. Coaxial driver wins that game always, but otherwise not necessarily...probably.

With simplified theory c-c = 1/2 wave length is the worst case for power response with equal DIs, and c-c = wave length at XO is the best case. Simply because sum with difference of 1/2 wave length is null and vertical +/-90 deg have the biggest weight in power calculation (due to dual orbit data to spherical intensity conversion). Early vertical reflections have significance too and DI of different radiators are not always equal => the smoothest DI and ERDI is found when c-c = 1.0-1.4 x wave length. This means that possibility of the worst DI is when c-c = 0.5-0.7 x wave length.

c-c studies are ridiculously easy with VituixCAD. Just load measurement data of the radiators, create ideal flat on axis response (with Optimizer and G(f) blocks) with estimated XO and tune driver's Y mm until combination of DI and ERDI is the best.

"Quote:
Originally Posted by DaveFred
3) Just your regular roundover or chamfer, the larger the better.
How different are roundovers vs. a chamfer?
Can you model chamfers with the diffraction tool?
What about square edges around the woofer and large "facets" cut around the tweeter instead of the larger roundovers/chamfer?"

Quite many questions and I don't know what "facet" is.
I prefer rounded chamfers, 45 deg and R>=32mm, both quite easy to manufacture. Tweeter should have very small effective baffle size to create directivity above typical XO frequency.

Diffraction tool is limited, but supports designing flat baffle area so that directivity dips and humps due to edges compensate directivity dips and humps of drivers and estimated combination of them assuming phase match at XO. Few tips:
- Do not increase directivity at XO with the box because phase matched XO does it anyway.
- Do not increase directivity below XO with the box because woofer cone does it anyway.
- Increase directivity above XO with the box if tweeter does not have wave guide or wave guide is small.

 

[pma]

Fwiw, if you can get two drivers to be less than 1/4 wl apart where they interact

... then make it 5/4 wl.

 

[MrPeabody]

Fwiw, if you can get two drivers to be less than 1/4 wl apart where they interact, they add coherently without cancellation notches and lobes.
It does take an alternative crossover shape to combine without the normal "all pass" phase shift but it is possible.
Tom

To say this in a way a little more precise, the vertical angles at which the notches occur are separated by at least 180 degrees if the vertical separation of the two drivers is less than 1/2 wavelength at the crossover frequency. The criterion that ctrl used is for the vertical separation distance to be less than the full wavelength. If the separation is less than 1/2 wavelength, the null will locate greater than +/- 90 degrees for the coherent crossover when the lobe pattern is symmetrical about the horizontal. There will be some attenuation at +/- 90 degrees, but not so great as with a full notch. If you make it less than 1/4 wavelength as you suggest, the amount of attenuation at +/- 90 degrees will be milder still, to the point of insignificance. Were it not for the reflections from the ceiling and the floor, the 1/2 wavelength criterion would likely be more than adequate.

 

[MrPeabody]

Good thread. Just wanted to add this...

FWIW, the rule of thumb I've always followed is 1/2 wavelength. At 2kHz that is about 3.38 inches (0.08m). Tough to do when talking CTC between a 6-inch midwoofer and a 1-inch dome tweeter but it is manageable. This is why when I see a speaker where a basket is cut to push the two drivers' CTC together, I immediately assume the company knows what they are doing. Otherwise, why spend the money to cut baskets or have custom molds when off-the-shelf parts will do.

View attachment 128863






Also, the graphic below provides a good illustration of the (significant, IMHO) difference when using the full-wavelength rule vs the half-wavelength rule. (Note: D= Diameter, in inches)

I think that the one-half wavelength criterion would be more than adequate were it not for the reflections from the ceiling and the floor. The little polar diagrams above you chart clearly suggest that this criterion should be adequate regardless. But I'm not sure those little polar diagrams are correct. Maybe it is for a specific crossover, but I'm not sure. Ordinarily, if the vertical spacing between the drivers is 1/2 wavelength, there will be a notch in the polar at +/- 90 degrees (for a phase coherent crossover where the lobe pattern is symmetrical above and below the horizontal). In the little polar diagram for lambda = 2D, there is no evidence at all of the notch that I think should be there.

 

[MrPeabody]

Thanks for the sims btw.

The LR4 and LR8 are what I was talking about. If I set the y-axis -115mm for the woofer in your vcad sim, the nulls are moved way off-axis and DI is smooth.

Am I breaking the sim or is it a matter of setting the c-to-c spacing to the XO you want to use if you want the nulls way off-axis?

The power response and the directivity index are more or less two ways of looking at the same thing, one being inverted vs. the other. There is always a dip in the power response for any phase-coherent crossover where the individual responses are both -6 dB at the crossover point. This is necessarily true because power is a scalar quantity that sums in the simple manner of simple addition for two drivers, and -6 dB for each driver means that power from each driver (individually) is half what it is nominally, far from the crossover point. -6 db implies twice halving of power (halving of SPL and voltage), i.e., that power for each driver is 1/4 the nominal value, thus combined power will be 1/2 the nominal value, thus a -3 dB response anomaly at the crossover point. It won't go away so long as the crossover is phase-coherent for the two drivers and so long as both are -6 dB at the crossover point, such that pressure response will be flat across the crossover frequency.

Additionally, I cannot get my head around the idea that there could be any possible advantage of increasing the vertical separation of the two drivers. Much less the idea that there would be one particular value (1.2 x wavelength) that would be optimal in some way. This only determines the vertical polar angles above and below the horizontal where the notches occur. When the vertical separation of the two drivers is increased, the angular spacing between the two notches decreases. The main forward lobe becomes squished, flatter.

Hmm. As I think about this, the one thing that comes to mind is that the idea might be for the nulls in the lobe pattern to be angled so that they hit the ceiling directly over the listener's head, such that the ceiling reflection is a uniform response. This would in fact be a useful thing to do, but it seems like it depends on too many other factors including the distance the listener is from the speakers. I don't generally like design principles that make assumptions about where the listener is seated relative to the speaker, especially when the assumption is with respect to the listener distance. I much prefer the idea of eliminating the nulls in the polar response by placing the two drivers adequately close together.