Ouch - that would rule it out for my use case of "the odd sum a few times a year"But the home license costs USD$195/yr.
-
WANTED: Happy members who like to discuss audio and other topics related to our interest. Desire to learn and share knowledge of science required. There are many reviews of audio hardware and expert members to help answer your questions. Click here to have your audio equipment measured for free!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Complex impedance load amp FR influence - WiiM Amp review by Erin
- Thread starter ctrl
- Start date
Great post. I would add that the curve tracing and modeling can also all be done using VituixCad, which is free.The frequency response of the Wiim Amp can be almost entirely predicted as a response of the LC output filter. So there isn't any big mystery as to how the Wiim Amp responds to "complex loads" (i.e. the response is highly predictable when the speaker impedance is known).
The L and C values from TI's Class D Amplifier LC Filter Design application note example works perfectly.
View attachment 352542
The filter L is: 11.25 μH
The filter C is: 2 * C_btl = 2 * 0.68 μF = 1.38 μF
R_load = R_btl/2 = R_speaker/2
The complex impedance of an inductor: Z_l = 1j * ω * L
The complex impedance of a capacitor: Z_c = -1j / (ω * C)
Using the voltage divider formula, the frequency response is given as:
View attachment 352558
The magnitude and phase of Z_spkr ( | Z_spkr | and angle( Z_spk r) ) are read from the impedance curve with help from WebPlotDigitizer and interpolated for the calculations.
Below are the plots of the digitized impedance magnitude and phase of Erin's "complex load":
View attachment 352553View attachment 352554
Here is the calculated frequency (magnitude) response, and it well matched Erin's measurement.
View attachment 352555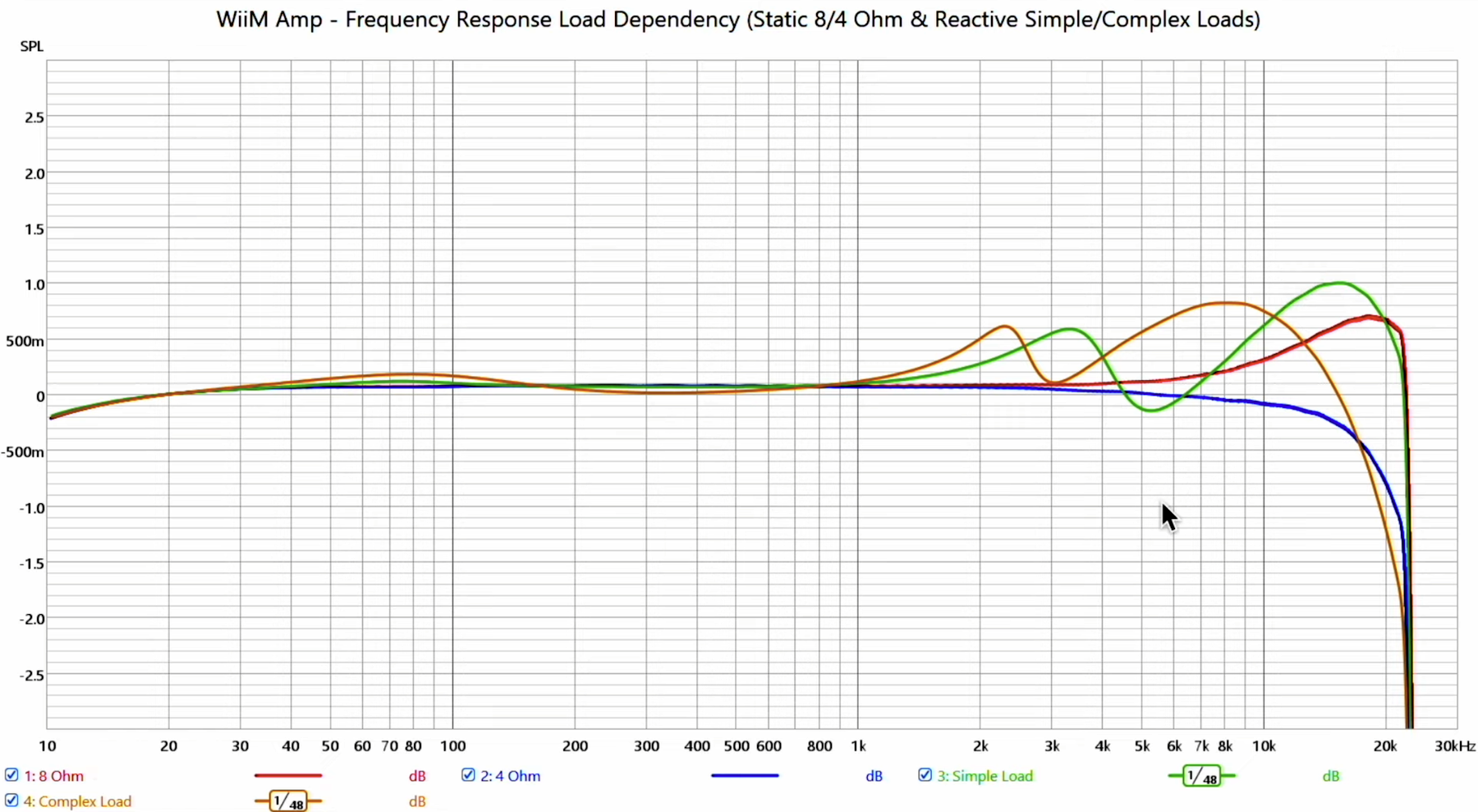
OP
- Thread Starter
- #103
The frequency response of the Wiim Amp can be almost entirely predicted as a response of the LC output filter.
The L and C values from TI's Class D Amplifier LC Filter Design application note example works perfectly.
Thanks @NTK for your efforts.
A few things are still not clear to me (sorry, I'm not an electronic expert), do I understand you correctly, in order to be able to carry out the simulation, you have to know which Class-D circuit and LC filter design the manufacturer of the Class-D amp used?
Because Erin provided the frequency response measurement of the amplifier with the complex load, were you able to decide which Class-D circuit and which LC filter design was used by the amp manufacturer?
If I understand you correctly, this unfortunately means that it is not possible to predict the frequency response behavior of any amplifier under a complex load, since one typically does not know the Class-D circuit and LC filter design of the manufacturer?
Below is the comparison of your simulation (dark blue) with Erin's frequency response measurement (brown/orange). The agreement is really good.
Are the deviations above 1kHz possibly due to the manufacturer using slightly different LC filter values?
How can it be explained that in the range of 20-200Hz, your simulation, unlike the measurement, shows no change in frequency response?
somebodyelse
Major Contributor
- Joined
- Dec 5, 2018
- Messages
- 3,759
- Likes
- 3,067
It's free for non-commercial use on a Pi. https://www.wolfram.com/raspberry-pi/Ouch - that would rule it out for my use case of "the odd sum a few times a year"

- Joined
- Oct 10, 2020
- Messages
- 806
- Likes
- 2,638
Note that you don't really need to know the implementation of the circuit; you just need to measure the amplifier's output impedance characteristic (magnitude and phase vs frequency) to be able to calculate its FR into any load.If I understand you correctly, this unfortunately means that it is not possible to predict the frequency response behavior of any amplifier under a complex load, since one typically does not know the Class-D circuit and LC filter design of the manufacturer?
This is why I'd personally love to see output impedance measurements in amplifier reviews...
I don't know anything about the design of the Wiim Amp output filter. For my calculations, I only used the values given in the TI App note I referenced in my earlier post, and they happened to match very well. My point is that the FR behavior is not caused by some mysterious complex interactions with the load that happened deep inside the class-d amp circuitry.Thanks @NTK for your efforts.
A few things are still not clear to me (sorry, I'm not an electronic expert), do I understand you correctly, in order to be able to carry out the simulation, you have to know which Class-D circuit and LC filter design the manufacturer of the Class-D amp used?
Because Erin provided the frequency response measurement of the amplifier with the complex load, were you able to decide which Class-D circuit and which LC filter design was used by the amp manufacturer?
If I understand you correctly, this unfortunately means that it is not possible to predict the frequency response behavior of any amplifier under a complex load, since one typically does not know the Class-D circuit and LC filter design of the manufacturer?
Below is the comparison of your simulation (dark blue) with Erin's frequency response measurement (brown/orange). The agreement is really good.
Are the deviations above 1kHz possibly due to the manufacturer using slightly different LC filter values?
How can it be explained that in the range of 20-200Hz, your simulation, unlike the measurement, shows no change in frequency response?
View attachment 354573
One thing I should point out is that the corner frequency of the LC is given as: fc = 1/( 2π √(L×C) ). If there is a capacitive component in the load impedance, the capacitive part will act in parallel with the output filter C, and since that will increase the effective filter C, it pushes the filter corner frequency (and the resonance peak) lower, and that, IMHO, is the most significant cause of the frequency response fluctuation.
For the low frequencies, the output LC filter, being a [Edit]
Last edited:
I don't know anything about the design of the Wiim Amp output filter. For my calculations, I only used the values given in the TI App note I referenced in my earlier post, and they happened to match very well. My point is that the FR behavior is not caused by some mysterious complex interactions with the load that happened deep inside the class-d amp circuitry.
One thing I should point out is that the corner frequency of the LC is given as: fc = 1/( 2π √(L×C) ). If there is a capacitive component in the load impedance, the capacitive part will act in parallel with the output filter C, and since that will increase the effective filter C, it pushes the filter corner frequency (and the resonance peak) lower, and that, IMHO, is the most significant cause of the frequency response fluctuation.
For the low frequencies, the output LC filter, being a high pass filter with a high fc, shouldn't matter much. Those response deviations are most likely due to different causes.
…except think you meant the output LC is a low pass filter.
If you have time, can you make a prediction of a common speaker (like the Elac dbr62) and plot the result?The frequency response of the Wiim Amp can be almost entirely predicted as a response of the LC output filter. So there isn't any big mystery as to how the Wiim Amp responds to "complex loads" (i.e. the response is highly predictable when the speaker impedance is known).
The L and C values from TI's Class D Amplifier LC Filter Design application note example works perfectly.
View attachment 352542
The filter L is: 11.25 μH
The filter C is: 2 * C_btl = 2 * 0.68 μF = 1.38 μF
R_load = R_btl/2 = R_speaker/2
The complex impedance of an inductor: Z_l = 1j * ω * L
The complex impedance of a capacitor: Z_c = -1j / (ω * C)
Using the voltage divider formula, the frequency response is given as:
View attachment 352558
The magnitude and phase of Z_spkr ( | Z_spkr | and angle( Z_spk r) ) are read from the impedance curve with help from WebPlotDigitizer and interpolated for the calculations.
Below are the plots of the digitized impedance magnitude and phase of Erin's "complex load":
View attachment 352553View attachment 352554
Here is the calculated frequency (magnitude) response, and it well matched Erin's measurement.
View attachment 352555
All users of this amp have EQ. Not wanting it is just silly.. we can stop the objectively good sound discussion right there… and yes, you have to measure, you should do that anyway. Passive impedance correction you have to measure as well
imagine wasting two filters to fix this amp being inadequate.
it's like saying buying a badly sounding headphone and then EQing it, except it's way easier to make an accurate amplifier than to make a good sounding headphone.
Yes! You are correct…except think you meant the output LC is a low pass filter.
Interesting - though out of date since noobs is no longer offered. I'll have to check my latest raspi OS install.It's free for non-commercial use on a Pi. https://www.wolfram.com/raspberry-pi/
Image them implementing more than a handful of PEQsimagine wasting two filters to fix this amp being inadequate.
Then good luck finding an alternative product with similar features and price with a better amp..it's like saying buying a badly sounding headphone and then EQing it, except it's way easier to make an accurate amplifier than to make a good sounding headphone.
Image them implementing more than a handful of PEQs
Then good luck finding an alternative product with similar features and price with a better amp..
Like the plethora of AVRs out there with the same A/B amplifier modules for the last 20 years?
Note that you don't really need to know the implementation of the circuit; you just need to measure the amplifier's output impedance characteristic (magnitude and phase vs frequency) to be able to calculate its FR into any load.
This is why I'd personally love to see output impedance measurements in amplifier reviews...
I think Amir has made his position clear, but if his AP had a better tool, sounds as though he might reconsider. Unless it changed since I owned, a the QA40x measures output impedance but does not do phase, so EAC is not able to do either.
Last edited:
Sokel
Master Contributor
- Joined
- Sep 8, 2021
- Messages
- 6,127
- Likes
- 6,206
The main rant about tube amps the last century apart from high THD+N (mostly inaudible with music,I have compared nice ones) was exactly that,load dependency and low power.
Are we going in circles?
For what?Price?
I don't think that's the way.
Are we going in circles?
For what?Price?
I don't think that's the way.
The main rant about tube amps the last century apart from high THD+N (mostly inaudible with music,I have compared nice ones) was exactly that,load dependency and low power.
Are we going in circles?
For what?Price?
I don't think that's the way.
It will get fixed as PFFB does not add much to the cost. My Dayton APA150 ($200) has mediocre SINAD but has handled many different speakers over the years. Works great for my shop but probably not a good nearfield amp.
Last edited:
They don’t have the same feature set, especially not for € 350, nor compact format. But yes, an AVR quickly becomes an interesting proposition if you have a bit more budget and can spare the room.Like the plethora of AVRs out there with the same A/B amplifier modules for the last 20 years?
It happens that I had a little of free time todayIf you have time, can you make a prediction of a common speaker (like the Elac dbr62) and plot the result?
Below is the FR plot and PDF of the Mathematica notebook is attached.
Yes. I saw your post in the Wiim Amp review thread. Your VCAD simulation results and mine for the JBL HDI-1600 matched very wellGreat post. I would add that the curve tracing and modeling can also all be done using VituixCad, which is free.

WiiM Amp Streaming Amplifier Review
I can't say I know what is typical for the speakers that really give these types of amps problems. But with the C-note impedance curve (simulated below), there is minimal wiggle except for the strong resonant peak, so pretty similar shape to the case of a pure resistor load. If you know of...
 www.audiosciencereview.com
www.audiosciencereview.com
Attachments
OP
- Thread Starter
- #119
Great post. I would add that the curve tracing and modeling can also all be done using VituixCad, which is free.
With the VCAD trace tool, you can only read the impedance frequency response. There is no way to read the impedance phase frequency response (AFAIK).
However, it seems that the impedance phase frequency response behaves almost as a minimal phase system, so the resulting phase error is relatively small.
Here is a comparison of the impedance phase frequency response of the measurement with the phase frequency response calculated by VCAD from the impedance measurement - see the orange arrows (please ignore the impedance curve, as the scaling is incorrect there).

If one is willing to accept slight impedance phase errors, the "SPL Trace" tool of VCAD can be used to read the impedance frequency response, and then the impedance + phase response can then be written into a file using the export function.
OP
- Thread Starter
- #120
So, I've adopted @NTK's idea about the low-pass filter of Class-D amplifier and simulated it in VCAD. This means that a passive filter was designed to closely match the frequency response for Erin's measurements of the Wiim-Amp with a complex load and a constant 8-ohm load.
Here's the effect of the filter with an 8-ohm load (orange measurement, red simulation):
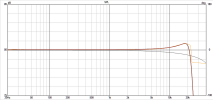
Here's the effect of the filter with Erin's complex load (orange measurement, red simulation):
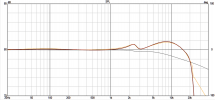
The filter used accurately reflects the load dependency of the WiimAmp (above 200Hz). This makes it easy to determine the approximate frequency response for any speaker loads - similar to what @NTK does, but without requiring Mathematica software, only VCAD.
The reason the simulation does not match in the low-frequency range below 200Hz is that the high-pass behavior (frequency response drop below 20Hz) of the amplifier is not simulated.
Here's the simulated frequency response of the WiimAmp when using ELAC DBR-62 speaker (accurate only above 200Hz):
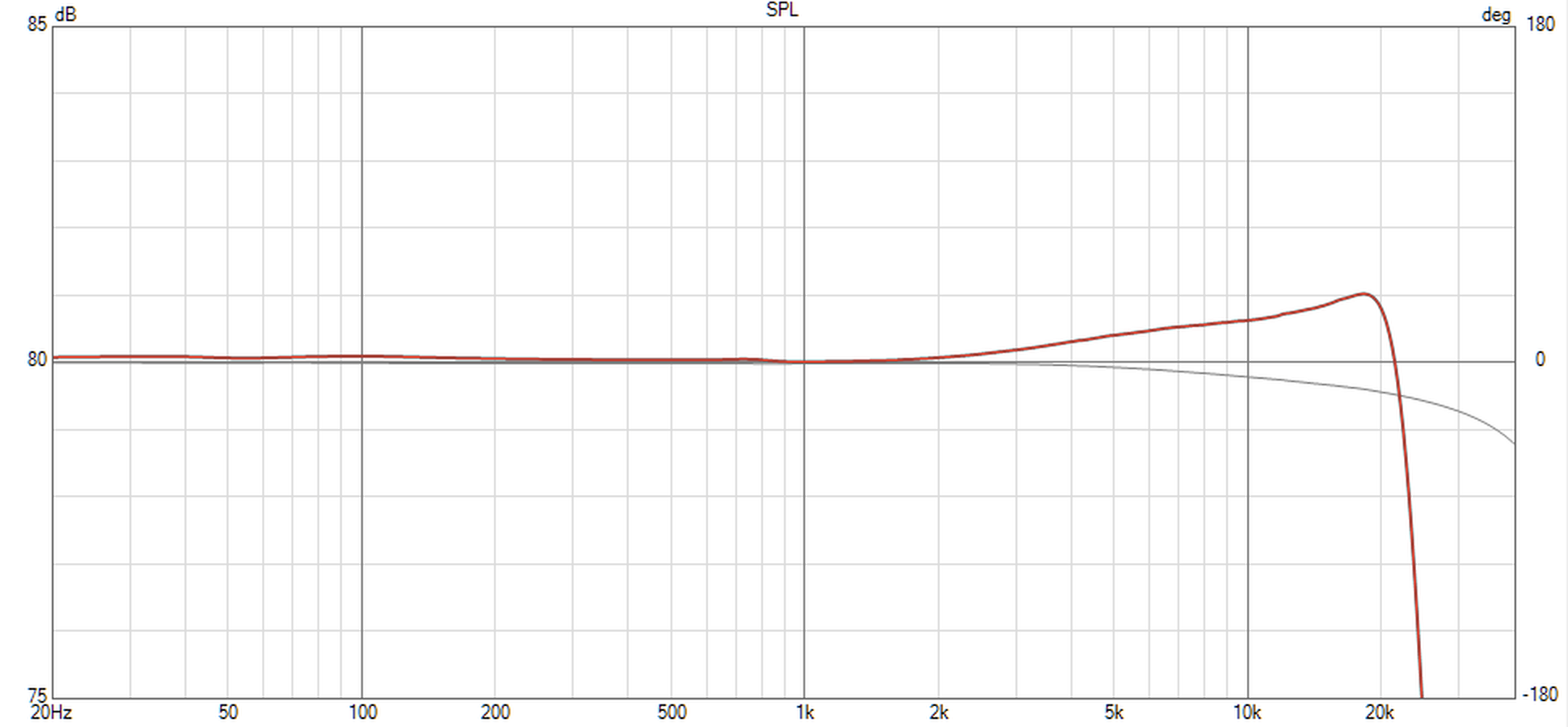
Think that's close to NTK's simulation in post#118.
Here's the simulated frequency response WiimAmp using JBL Studio 590 speaker (accurate only above 200Hz):
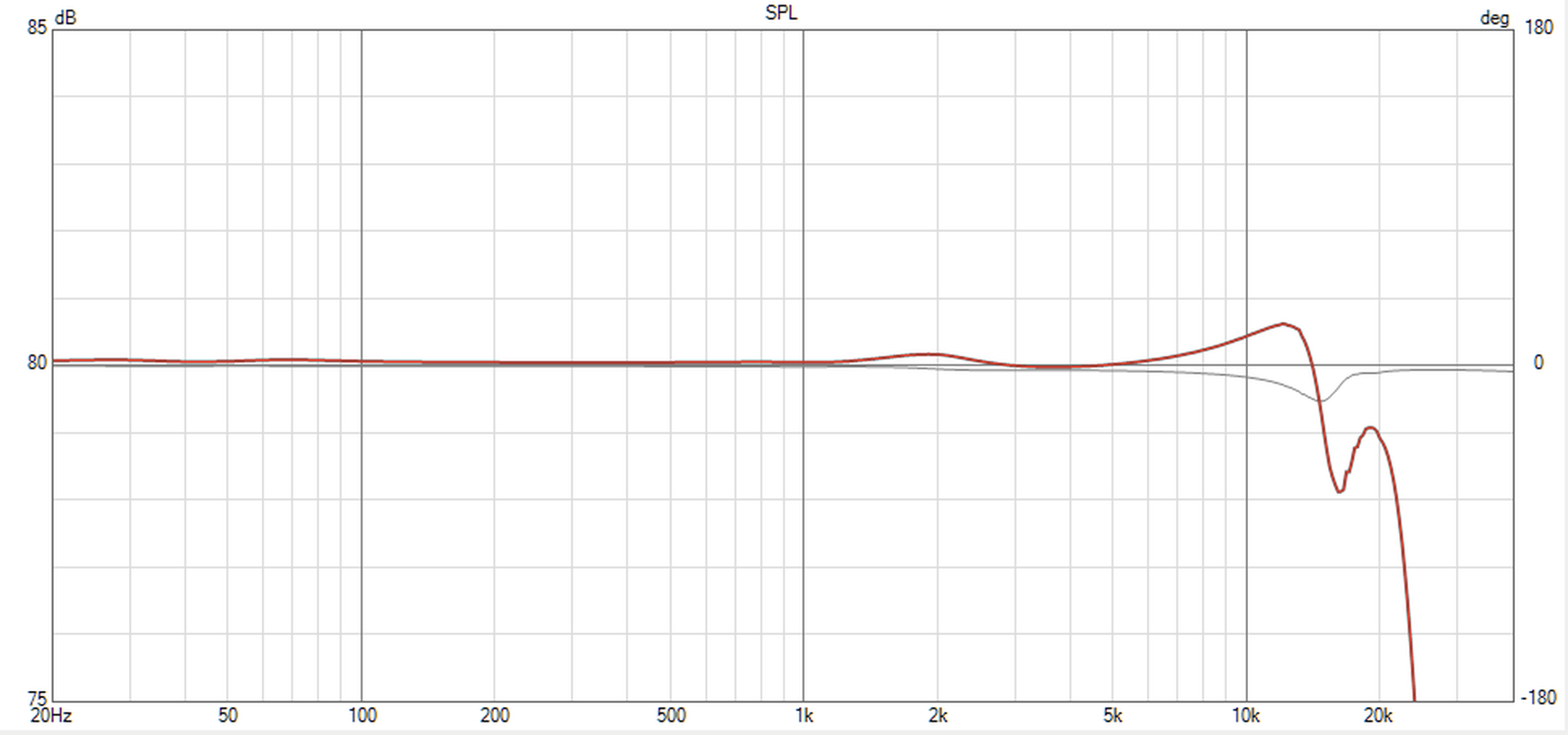
Here's the simulated frequency response WiimAmp using JBL Studio 698 speaker (accurate only above 200Hz):
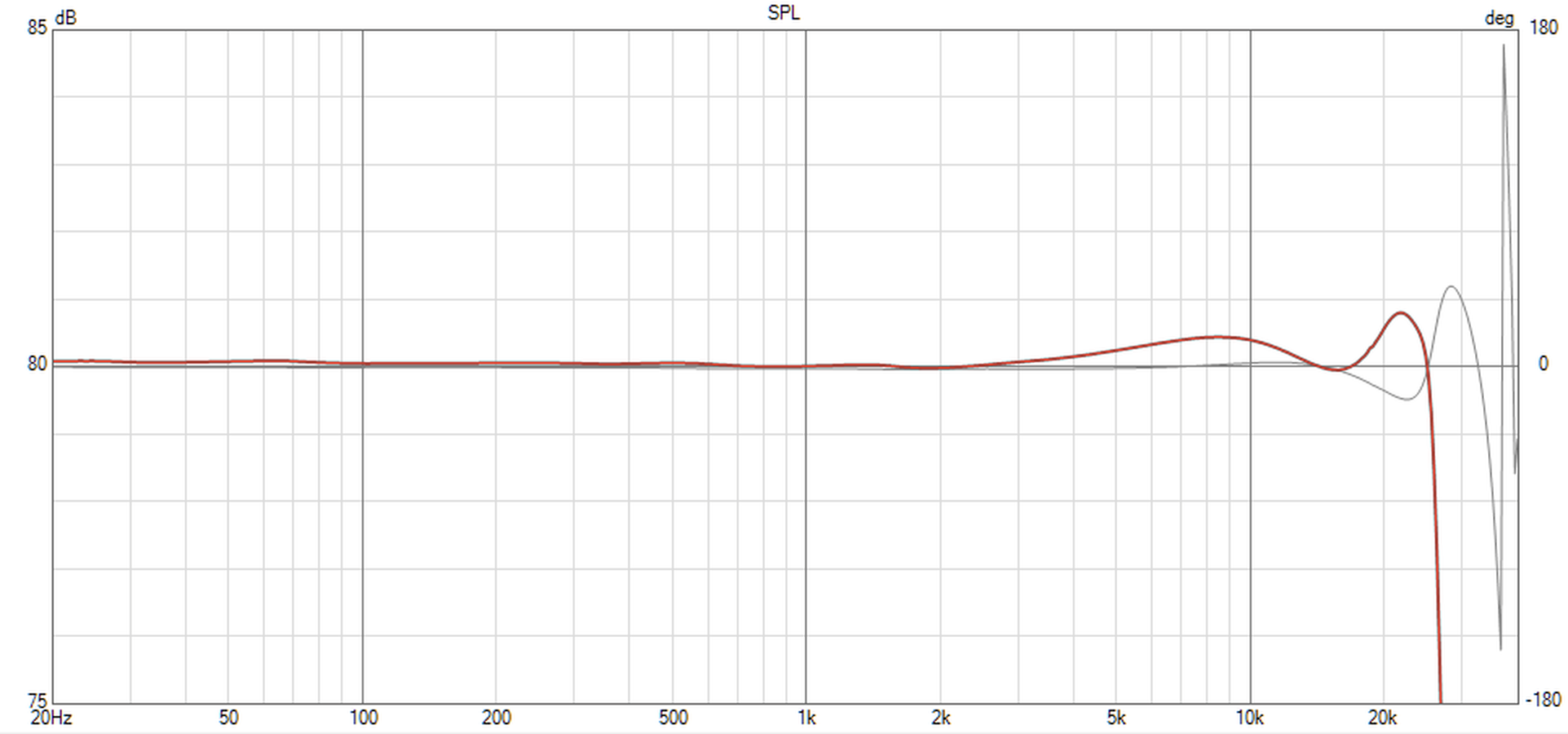
Here's the simulated frequency response WiimAmp using Wharfedale Aura 2 speaker (accurate only above 200Hz):
Attached you will find the VCAD project. With this, anyone can conduct simulations of speakers on the WiimAmp amplifier (provided my considerations for the simulation are correct ).
).
In the Driver tab of VCAD, simply select the speaker impedance you want to simulate. If you delete the impedance, VCAD defaults to a constant 8-ohm load.
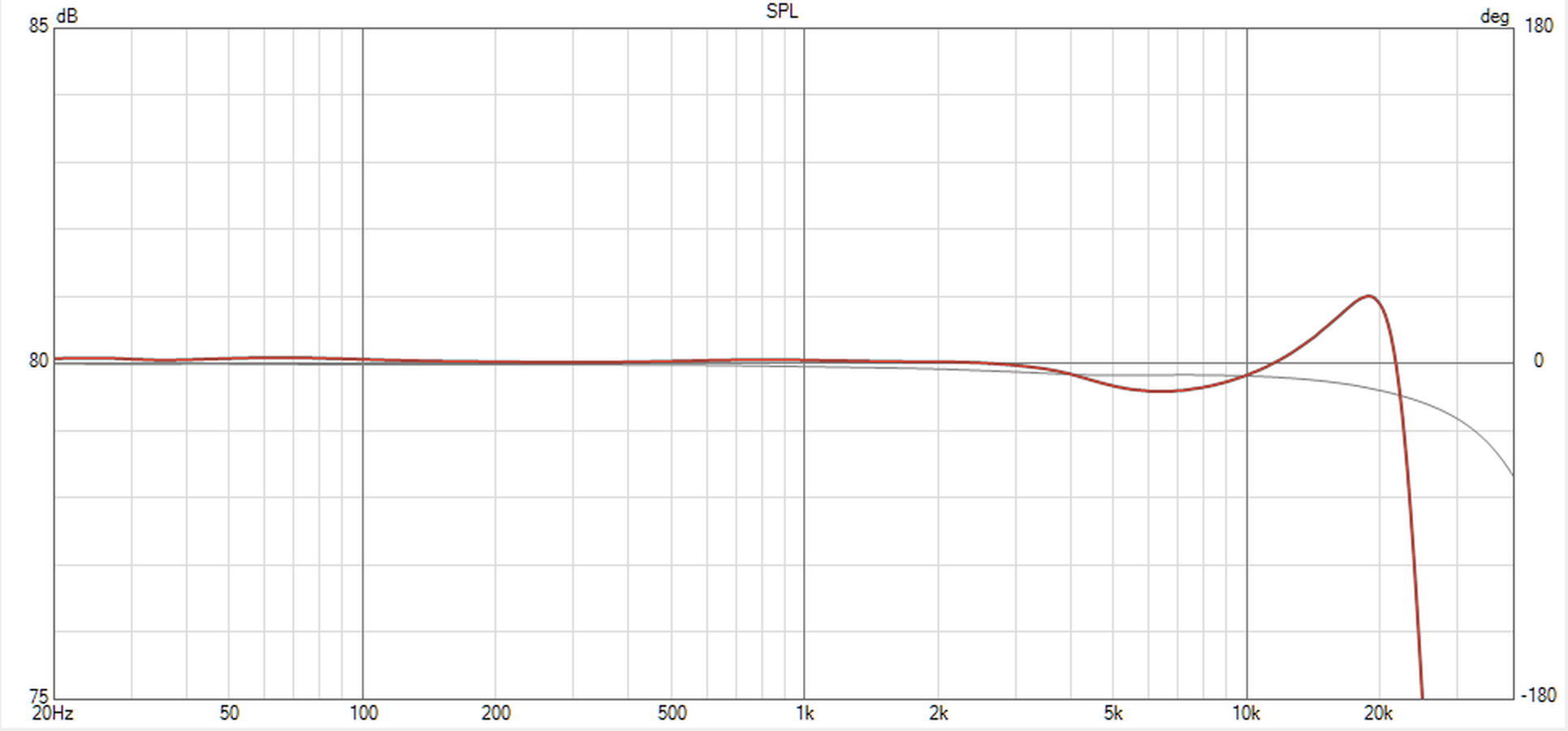
UPDATE:
Modified VCAD project attachment to better simulate different speaker load effects on wiimAmp FR. The simulation provides useful data in the 200-12000Hz range. Above 12kHz the simulated FR of the amp differs from the measurement - my guess is that the impedance phase response no longer behaves like a minimum phase system, so when using only the impedance frequency response for the simulation and calculate the impedance phase response, it will cause errors in the simulated amp FR above 12kHz.
Here's the effect of the filter with an 8-ohm load (orange measurement, red simulation):

Here's the effect of the filter with Erin's complex load (orange measurement, red simulation):

The filter used accurately reflects the load dependency of the WiimAmp (above 200Hz). This makes it easy to determine the approximate frequency response for any speaker loads - similar to what @NTK does, but without requiring Mathematica software, only VCAD.
The reason the simulation does not match in the low-frequency range below 200Hz is that the high-pass behavior (frequency response drop below 20Hz) of the amplifier is not simulated.
Here's the simulated frequency response of the WiimAmp when using ELAC DBR-62 speaker (accurate only above 200Hz):
Think that's close to NTK's simulation in post#118.
Here's the simulated frequency response WiimAmp using JBL Studio 590 speaker (accurate only above 200Hz):
Here's the simulated frequency response WiimAmp using JBL Studio 698 speaker (accurate only above 200Hz):
Here's the simulated frequency response WiimAmp using Wharfedale Aura 2 speaker (accurate only above 200Hz):
Attached you will find the VCAD project. With this, anyone can conduct simulations of speakers on the WiimAmp amplifier (provided my considerations for the simulation are correct
In the Driver tab of VCAD, simply select the speaker impedance you want to simulate. If you delete the impedance, VCAD defaults to a constant 8-ohm load.

UPDATE:
Modified VCAD project attachment to better simulate different speaker load effects on wiimAmp FR. The simulation provides useful data in the 200-12000Hz range. Above 12kHz the simulated FR of the amp differs from the measurement - my guess is that the impedance phase response no longer behaves like a minimum phase system, so when using only the impedance frequency response for the simulation and calculate the impedance phase response, it will cause errors in the simulated amp FR above 12kHz.
Attachments
Last edited:
Similar threads
- Replies
- 2
- Views
- 365
- Replies
- 19
- Views
- 1K
- Replies
- 178
- Views
- 9K
- Replies
- 3
- Views
- 360
- Replies
- 775
- Views
- 129K
