Room interactions are often discussed as one of the primary reasons similar (or even dissimilar) systems sound different. If you read the “Reflections and DACs” article you saw how reflections and standing waves can interact along a transmission line. As it happens, sound waves in a room also interact, affecting the amplitude of sound you hear at different frequencies. Sound waves from more than one source (for example, two speakers) will meet and interact. Sometimes they add, sometimes they subtract (cancel), but there will be interactions in any room. “Ah, but what about absorption?” you might ask. Ah, but remember I said “more than one source”. If I put two speakers in a perfect anechoic chamber, absorbing all sound when it interacts with any surface (walls, floor, ceiling), there are still those two sources to consider. If I sit between them, waves from one interact with waves from the other, despite having no other reflections to contend with. See Figure 1; sound waves from the two speakers spread out and interact at the listener’s location.

Figure 1. Sound wave interaction.
Depending upon their phase, the sound waves may add constructively, making the sound louder, or destructively, sounding quieter. The phase depends upon the source, naturally, but also the frequency and distance from the speakers. Take a look at Figure 2, showing three different frequencies (fo, 2fo, and 5.9fo). The vertical axis shows amplitude and the horizontal axis distance. All is relative for this example.
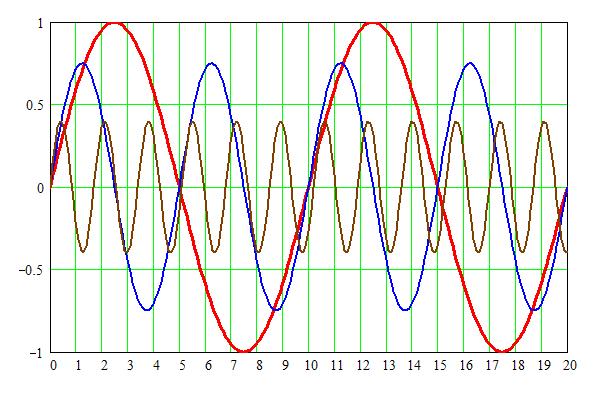
Figure 2. Amplitude vs. distance for three frequencies.
All three waves are launched at the same instant and in phase (this is not generally true). Now, there are several interesting observations we can make from this picture:
At an arbitrary distance, the sound waves do not line up perfectly. This is the way the world works and is not really important, so long as the phase relationship is maintained. That is, if your components (from source through speakers) alter the phase/frequency relationship, then what you hear may be different from what was originally recorded. However, even if that is not true, chances are you won’t notice… As an aside, speakers typically dominate the phase picture, and speakers with excellent pulse (or impulse) characteristics do best at maintaining phase relationships across all frequencies (linear phase, constant group delay, to be technical). I do like my Magnepans!
As frequency increases, the peaks and valleys get closer. At 20 Hz there are over 56 feet from peak to peak; at 20 kHz the distance from peak to peak is less than an inch. At low frequencies, the waves are longer than most rooms and room modes dominate. At high frequencies, most any little surface will cause reflections, breaking up the waves so that by the time they reach you the reflections are pretty random with respect to the source and don’t really bother us. In between, the same sound from two different sources interacts as a function of frequency (actually wavelength, velocity of sound/frequency) and distance. If we are sitting such that two peaks interact, the sound will be louder; if a positive peak and negative peak interact they will cancel and no sound is heard at that frequency. While perfect cancellation in the real world is rare, deep nulls and large peaks do occur. The effect looks like the teeth in a comb, and thus the name “comb filter effects”. Unfortunately, comb filter effects tend to be worst right through the middle of the audio band, right where we hear best. When you move your head an inch, and the sound changes by a mile, that’s almost always what is causing the effect. The good news is that sound absorbers and diffusers can go a long way toward reducing comb filter effects, and proper speaker positioning minimizes interactions from the desired direct sources (your speakers).
Finally, when the sound wave hits a reflecting surface, it inverts and takes off at an angle equal to the incoming angle but on the other side: it makes a triangle. For the simplest case, consider a constant sound wave that comes from the speaker and hits the back wall, coming back along the same path but inverted (180 degrees out of phase). It’s like a mirror image of the sound… It travels along interacting with the incoming wave, sometimes adding, sometimes subtracting. Think of sitting somewhere in Figure 1 while signals bounce around, creating peaks and valleys at your listening position. What we hear depends upon where we sit with respect to the distance from the wall, and the frequency of the sound.
If we have a sound source in a closed room, the frequencies at which interactions occur (the modes) can be predicted since the dimension are known. Since we know the velocity of sound for a given frequency, we can calculate wavelengths, and in turn predict the modes of that room. Those are the frequencies at which peaks and valleys will occur. These peaks and valleys will occur at integer submultiples of the room’s dimensions, and even multiples generally cause the biggest problems. Thus sitting in the exact center of the room is where we are most likely to have problems with them. That is also the reason many sources suggest sitting 1/3 from either wall in the longest dimension of the room to minimize the impact of the lowest mode.
Calculating room modes is straight-forward if somewhat tedious:
Fmode = v/2 * m / D where
Fmode is the frequency of the mode
v is the velocity of sound (1130 ft/sec in dry air at sea level)
m is the mode (an integer: 1, 2, 3, …)
D is the room dimension (width, length, height)
The fundamental mode (m = 1) creates a standing wave in the middle of that dimension, a peak or null (usually a null, but it is sometimes hard to predict which as the modes increase). A mode of two indicates a wave that has traveled twice along that dimension, and so forth. There are tangential and oblique modes reflecting from other dimensions and such; it can get complicated quickly. For now, consider a simple room with dimensions 10’ W x 20’ L x 9’ H and calculate the first few modes in each dimension:
Fmode = (28, 57, 57, 63, 85, 113, 113, 126, 141, 170, 170, 188, 198, 226, 226, 251) Hz
These are frequencies at which sound in the room will peak or null. Note that peaks can easily reach 10 dB (10 times) or more, but physical factors (absorption, wall vibrations, etc.) usually prevent peaks much larger than that. Nulls due to cancellation can be quite deep; 30 dB (1/1000) or more is not uncommon. Thus, fixing the nulls is often harder than bringing down the peaks. It is often easier to move the listening position…
Note that several frequencies are duplicated. This is because 20’ is an integer multiple of 10’, leading to multiple modes at the same frequency. This will exaggerate the effects at those frequencies, and indicates why good sound design requires room dimensions that are not multiples. Prime numbers are often used to prevent mode doubling.
Because closely-spaced modes are not heard as separate frequencies, knowing the difference frequency (Fd) between successive nodes is useful:
Fd = (28, 0, 6, 22, 28, 0, 13, 16, 28, 0, 19, 9, 28, 0, 25) Hz
Most texts agree that differences of 10 Hz or less are problematic as our ear/brain system does not separate them, making one big dip or peak. This room clearly has several problem frequencies…
Sound absorption or diffusion can be used to reduce or “break up” room modes and reduce their impact on frequency response. Either way, they must be physically large to handle low-frequency problems due to the very long wavelengths involved. This is why solving bass problems requires large diffusers and/or a lot of bass traps. Other folk, such as our own Ethan Winer, are better equipped to discuss mitigation of these modes in your room. His website, www.realtraps.com, also has a calculator to help determine the modes of your room. There are numerous other calculators online.
Reading back, this may a bit hard to follow, but hopefully presents a picture of room modes and why they matter.
HTH - Don

Figure 1. Sound wave interaction.
Depending upon their phase, the sound waves may add constructively, making the sound louder, or destructively, sounding quieter. The phase depends upon the source, naturally, but also the frequency and distance from the speakers. Take a look at Figure 2, showing three different frequencies (fo, 2fo, and 5.9fo). The vertical axis shows amplitude and the horizontal axis distance. All is relative for this example.

Figure 2. Amplitude vs. distance for three frequencies.
All three waves are launched at the same instant and in phase (this is not generally true). Now, there are several interesting observations we can make from this picture:
At an arbitrary distance, the sound waves do not line up perfectly. This is the way the world works and is not really important, so long as the phase relationship is maintained. That is, if your components (from source through speakers) alter the phase/frequency relationship, then what you hear may be different from what was originally recorded. However, even if that is not true, chances are you won’t notice… As an aside, speakers typically dominate the phase picture, and speakers with excellent pulse (or impulse) characteristics do best at maintaining phase relationships across all frequencies (linear phase, constant group delay, to be technical). I do like my Magnepans!
As frequency increases, the peaks and valleys get closer. At 20 Hz there are over 56 feet from peak to peak; at 20 kHz the distance from peak to peak is less than an inch. At low frequencies, the waves are longer than most rooms and room modes dominate. At high frequencies, most any little surface will cause reflections, breaking up the waves so that by the time they reach you the reflections are pretty random with respect to the source and don’t really bother us. In between, the same sound from two different sources interacts as a function of frequency (actually wavelength, velocity of sound/frequency) and distance. If we are sitting such that two peaks interact, the sound will be louder; if a positive peak and negative peak interact they will cancel and no sound is heard at that frequency. While perfect cancellation in the real world is rare, deep nulls and large peaks do occur. The effect looks like the teeth in a comb, and thus the name “comb filter effects”. Unfortunately, comb filter effects tend to be worst right through the middle of the audio band, right where we hear best. When you move your head an inch, and the sound changes by a mile, that’s almost always what is causing the effect. The good news is that sound absorbers and diffusers can go a long way toward reducing comb filter effects, and proper speaker positioning minimizes interactions from the desired direct sources (your speakers).
Finally, when the sound wave hits a reflecting surface, it inverts and takes off at an angle equal to the incoming angle but on the other side: it makes a triangle. For the simplest case, consider a constant sound wave that comes from the speaker and hits the back wall, coming back along the same path but inverted (180 degrees out of phase). It’s like a mirror image of the sound… It travels along interacting with the incoming wave, sometimes adding, sometimes subtracting. Think of sitting somewhere in Figure 1 while signals bounce around, creating peaks and valleys at your listening position. What we hear depends upon where we sit with respect to the distance from the wall, and the frequency of the sound.
If we have a sound source in a closed room, the frequencies at which interactions occur (the modes) can be predicted since the dimension are known. Since we know the velocity of sound for a given frequency, we can calculate wavelengths, and in turn predict the modes of that room. Those are the frequencies at which peaks and valleys will occur. These peaks and valleys will occur at integer submultiples of the room’s dimensions, and even multiples generally cause the biggest problems. Thus sitting in the exact center of the room is where we are most likely to have problems with them. That is also the reason many sources suggest sitting 1/3 from either wall in the longest dimension of the room to minimize the impact of the lowest mode.
Calculating room modes is straight-forward if somewhat tedious:
Fmode = v/2 * m / D where
Fmode is the frequency of the mode
v is the velocity of sound (1130 ft/sec in dry air at sea level)
m is the mode (an integer: 1, 2, 3, …)
D is the room dimension (width, length, height)
The fundamental mode (m = 1) creates a standing wave in the middle of that dimension, a peak or null (usually a null, but it is sometimes hard to predict which as the modes increase). A mode of two indicates a wave that has traveled twice along that dimension, and so forth. There are tangential and oblique modes reflecting from other dimensions and such; it can get complicated quickly. For now, consider a simple room with dimensions 10’ W x 20’ L x 9’ H and calculate the first few modes in each dimension:
Fmode = (28, 57, 57, 63, 85, 113, 113, 126, 141, 170, 170, 188, 198, 226, 226, 251) Hz
These are frequencies at which sound in the room will peak or null. Note that peaks can easily reach 10 dB (10 times) or more, but physical factors (absorption, wall vibrations, etc.) usually prevent peaks much larger than that. Nulls due to cancellation can be quite deep; 30 dB (1/1000) or more is not uncommon. Thus, fixing the nulls is often harder than bringing down the peaks. It is often easier to move the listening position…
Note that several frequencies are duplicated. This is because 20’ is an integer multiple of 10’, leading to multiple modes at the same frequency. This will exaggerate the effects at those frequencies, and indicates why good sound design requires room dimensions that are not multiples. Prime numbers are often used to prevent mode doubling.
Because closely-spaced modes are not heard as separate frequencies, knowing the difference frequency (Fd) between successive nodes is useful:
Fd = (28, 0, 6, 22, 28, 0, 13, 16, 28, 0, 19, 9, 28, 0, 25) Hz
Most texts agree that differences of 10 Hz or less are problematic as our ear/brain system does not separate them, making one big dip or peak. This room clearly has several problem frequencies…
Sound absorption or diffusion can be used to reduce or “break up” room modes and reduce their impact on frequency response. Either way, they must be physically large to handle low-frequency problems due to the very long wavelengths involved. This is why solving bass problems requires large diffusers and/or a lot of bass traps. Other folk, such as our own Ethan Winer, are better equipped to discuss mitigation of these modes in your room. His website, www.realtraps.com, also has a calculator to help determine the modes of your room. There are numerous other calculators online.
Reading back, this may a bit hard to follow, but hopefully presents a picture of room modes and why they matter.
HTH - Don
Last edited by a moderator:
