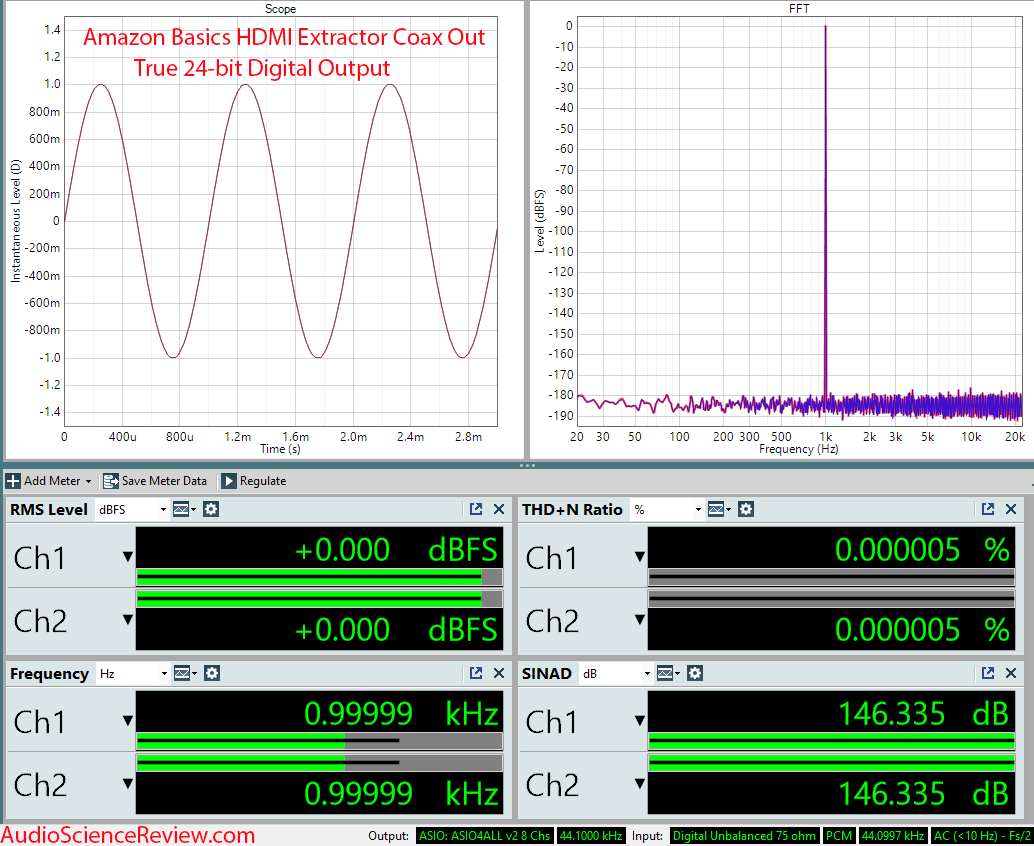
A steady sine wave tone is useful for various testing applications. A PCM encoded wave file can hold a representation of a sine wave, but often it's not perfect due to quantization loss when sine values are converted to integer sample values. The sine function generally produces irrational values, and an irrational value can't be digitized without loss. But Niven's theorem points out 3 special cases where sine is rational. If the PCM sine wave file is constructed using the rational values from Niven's theorem, quantization rounding loss can be avoided, allowing the PCM wav file to describe a sine wave perfectly. When such a constructed PCM sine wave file is played back, the only imperfections are due to equipment limitations, and not the wav file itself. Here is more information.
The effect of quantization loss on the spectrum of PCM sine waves has been thoroughly studied starting in the 1940s. But the focus is on real-world use, such as voice signals. I have yet to see anyone point out the 3 very special cases of sampling rate to sine frequency of 3, 4, and 6 that are useful for generating pure tones.
The PCM wave files for these 3 cases contain the following patterns, repeated indefinitely:
0 1 -1
0 1 0 -1
0 1 1 0 -1 -1
The effect of quantization loss on the spectrum of PCM sine waves has been thoroughly studied starting in the 1940s. But the focus is on real-world use, such as voice signals. I have yet to see anyone point out the 3 very special cases of sampling rate to sine frequency of 3, 4, and 6 that are useful for generating pure tones.
The PCM wave files for these 3 cases contain the following patterns, repeated indefinitely:
0 1 -1
0 1 0 -1
0 1 1 0 -1 -1