board
Senior Member
- Joined
- Apr 24, 2019
- Messages
- 326
- Likes
- 251
I like to think that I understand how digital audio works pretty well, but please help me understand this:
I was reading these measurements from Stereophile:
 www.stereophile.com
www.stereophile.com
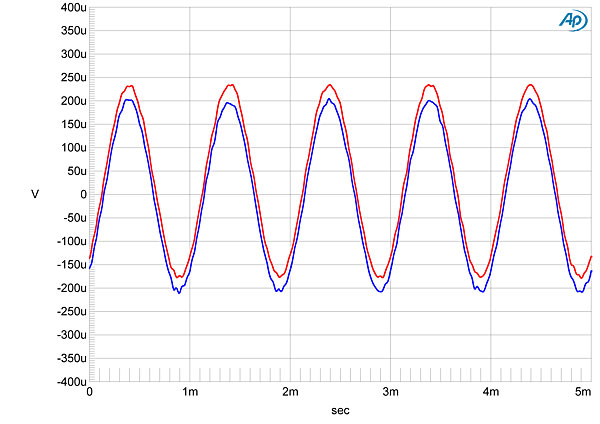
Figure 6 shows an undithered 16-bit tone, whereas figure 7 shows the same with 24 bit:
"[T]he M51's reproduction of an undithered 16-bit tone at exactly –90.31dBFS was essentially perfect (fig.6), with a symmetrical waveform and the Gibbs Phenomenon "ringing" on the waveform tops well defined. With 24-bit data, the M51 produced a superbly defined sinewave (fig.7). "
Figure 6:
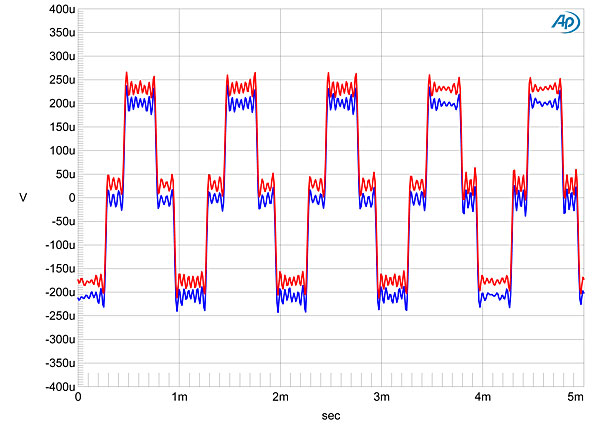
Figure 7:
Why are the two waves so different between 16-bit and 24-bit?
I was reading these measurements from Stereophile:
NAD M51 Direct Digital D/A converter Measurements
Sidebar 3: Measurements I used Stereophile's loan sample of the top-of-the-line Audio Precision SYS2722 system to measure the NAD M51 (see www.ap.com and the January 2008 "As We See It"; for some tests, I also used my vintage Audio Precision System One Dual Domain.
Figure 6 shows an undithered 16-bit tone, whereas figure 7 shows the same with 24 bit:
"[T]he M51's reproduction of an undithered 16-bit tone at exactly –90.31dBFS was essentially perfect (fig.6), with a symmetrical waveform and the Gibbs Phenomenon "ringing" on the waveform tops well defined. With 24-bit data, the M51 produced a superbly defined sinewave (fig.7). "
Figure 6:
Figure 7:
Why are the two waves so different between 16-bit and 24-bit?
