- Thread Starter
- #21
ADDENDUM
Crossover distortion analysis
Let's study the so-called crossover distortion, generated by class B amplifiers and to a lesser extent by class AB. In short, in these circuits the positive and negative values of the signal are amplified by different active elements. Given the non-simultaneity of switching off one chain and switching on the other, the type of distortion in question is generated in the crossing through the 0 of the signal, where small variations in the signal around 0 (gap) are not amplified correctly. The transfer curve with unit gain is exemplified in the following figure (top right), with an "exaggerated" gap of 0.1 to better show the trend; it is not represented by a polynomial, but still a continuous function of C^infinity class, with a very pronounced "elbow".
Fig. 29 - Crossover Distortions: Transfer Function, Harmonic Distortions, Time behaviour.
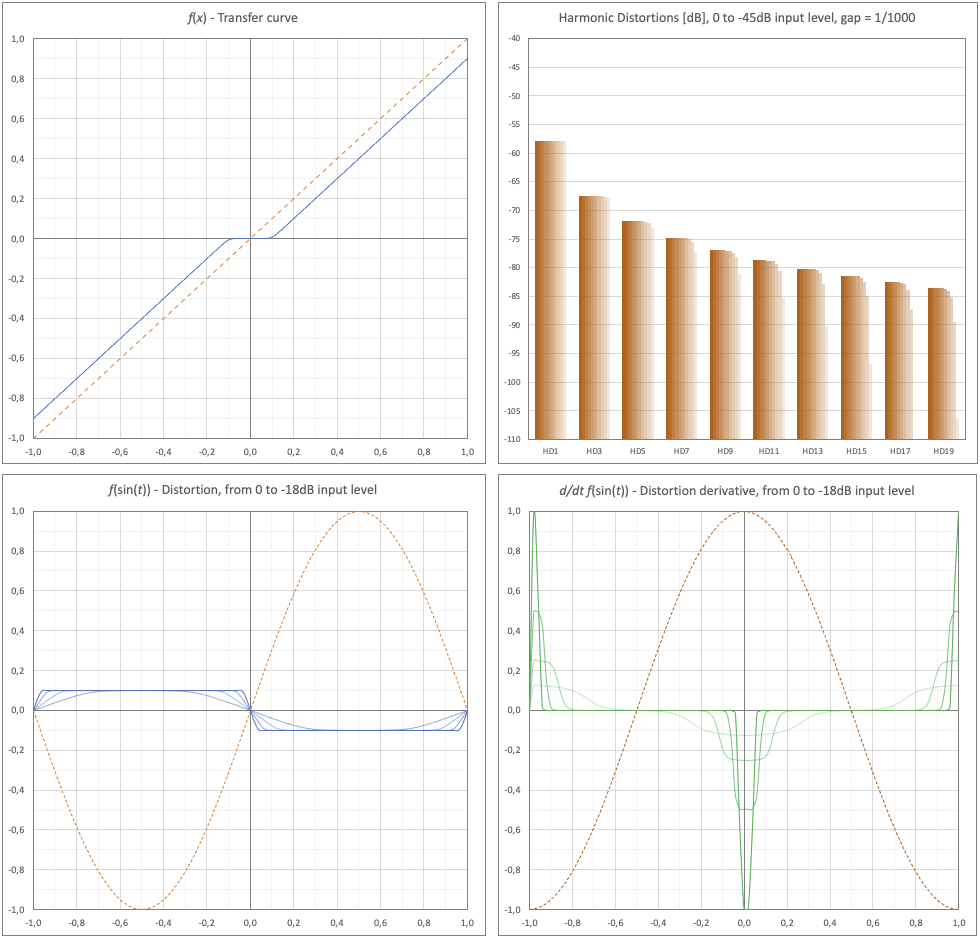
In the other graphs the classic values for a pure tone; we have:
- Bottom left: always exaggerating, the shape of the distortions as the input level decreases, with the same amplification (effect equivalent to increasing the gap, then scaling the module by the same amount). Basically, it is noted that a sort of square wave is added to the signal, in counter-phase with respect to the signal. The rising and falling edges are steeper the smaller the gap, and here they have a "soft" shape, given the simple course of the sinusoid.
- Bottom right: derivative of the distortion, where the abrupt variations in correspondence to the "edges" are evident (i.e. in the passage from values lower than the gap to the higher ones). This results in high order harmonics in the distortion.
- Top right: the trend of harmonic distortions (absolute values) as the signal level decreases, with gap = 1/1000. Only odd harmonics are present, including a contribution to the fundamental (HD1), with a typical square wave trend. As the signal level decreases, the low-order harmonic distortions remain almost constant, while the higher ones decrease. At the limit, the distortion "tends" to the original signal in counter-phase.
It is therefore not new that this type of distortions are higher (as a ratio) at low volumes: in the example we go from a True-THD = -57dB for 0dB to a True-THD = -17dB for -40dB.
For a complex signal, the square wave becomes more irregular. The following figure shows the usual “music-like” signal, where the original signal is shown at the top, and the distortion, amplified by 40dB, at the bottom.
For a complex signal, the square wave becomes more irregular. The following figure shows the usual “music-like” signal, where the original signal is shown at the top, and the distortion, amplified by 40dB, at the bottom.
Fig. 30 - Crossover distortion, Time Simulation - gap = 1/1000.
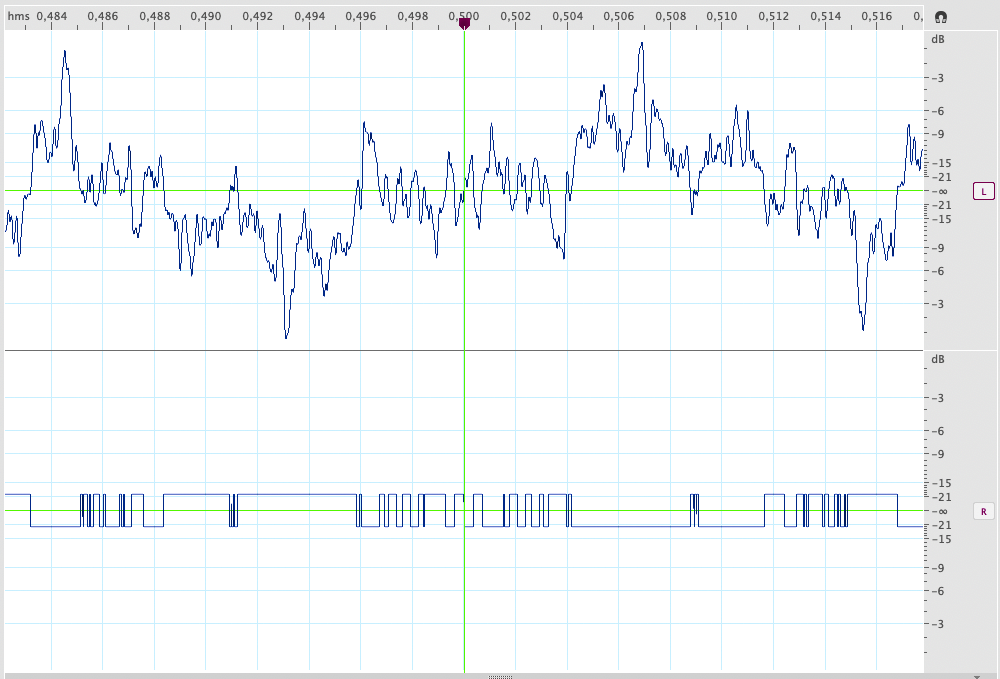
Basically, the distortion will be equal and opposite to the original signal as long as its absolute value is less than the gap; it will assumes the gap value (positive or negative) for all other values.
Before analyzing the graphs relating to DSA, PSD and PCD, it should be stated that here the dependence on the distribution of the test signal levels is even more important than in the previous cases. As reported in fig. 7a, the probability distribution curve is in fact very different for a sinusoidal signal and for the music-like signal. The simple and regular sinusoidal signal is statistically found just around 0, while it "frequents" much more the values close to the extremes. Quite the opposite is the density function for real signals, which generally approximates a Gaussian curve. Therefore, it is clear that the amount of signal below the gap is statistically greater in the case of real signals.
Let's now look in detail at the new indicators, DSA, PSD and PCD with the music-like signal. Always with a gap = 1/1000 and gain 0dB you have the curves in fig. 31.Before analyzing the graphs relating to DSA, PSD and PCD, it should be stated that here the dependence on the distribution of the test signal levels is even more important than in the previous cases. As reported in fig. 7a, the probability distribution curve is in fact very different for a sinusoidal signal and for the music-like signal. The simple and regular sinusoidal signal is statistically found just around 0, while it "frequents" much more the values close to the extremes. Quite the opposite is the density function for real signals, which generally approximates a Gaussian curve. Therefore, it is clear that the amount of signal below the gap is statistically greater in the case of real signals.
Fig. 31 - PSD, PCD and DSA for crossover distortion - gap = 1/1000.
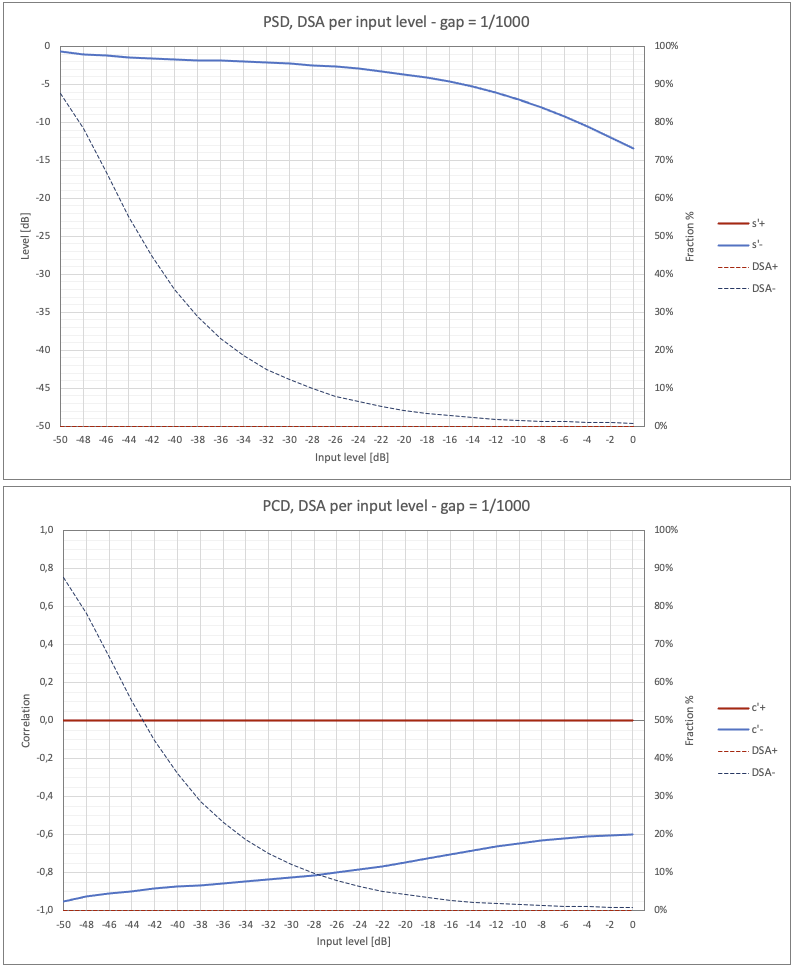
Both DSA curves are plotted in the graphs, both that relating to the fraction of expanded transients (DSA+) and that relating to compressed ones (DSA-). This is because the sum of DSA+ and DSA- does not give 100% here as in the previous cases: the missing part, the most conspicuous, is relative to the part of the signal whose transients are not altered, that is the one where its absolute value is above the gap value. Since PSD and PCD refer to transients, they will describe the behavior of only small parts of the distortion, i.e. only those where the signal is below the gap. In detail:
- The DSA+ is always equal to 0, indicating that there are no expanded transients; therefore PSD+ and PCD+ will also be null.
- The DSA- starts from very small values for high levels of the signal (on the right), to increase as the level decreases, where ever larger parts of the signal are below the level of the gap. In fact, here the DSA- represents the signal fraction below (in absolute value) to the gap.
- When the DSA- increases, both the energy associated with the compressed transients (PSD-) and the negative correlation (PCD-) increase in value, since they "include" more of the original signal and the edges effect for transients decreases. The PSD- comes to be equal to the signal and the PCD- equal to -1 (in phase opposition).
For comparison, the following figure shows the same indicators when the gap is 10 times smaller. In fact, we have the same curves as in fig. 31, shifted 20dB (10 times) to the left.
Fig. 32 - PSD, PCD and DSA for crossover distortion - gap = 1/10000.
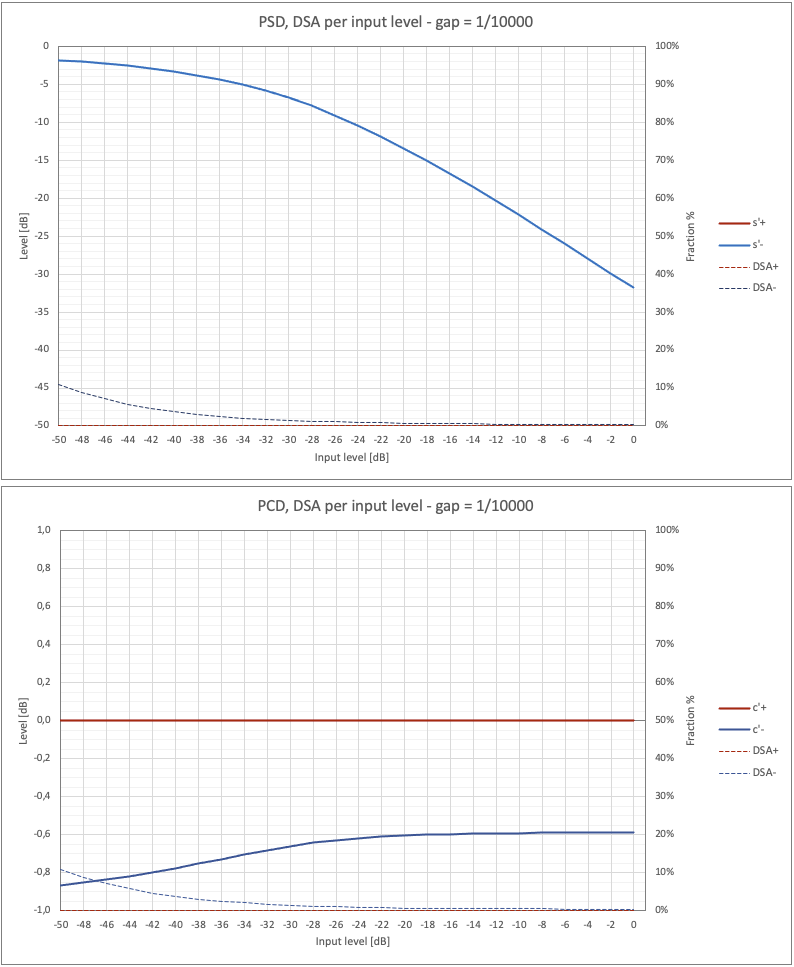
Therefore, the crossover distortion, if small, acts on very limited fractions of transients. However, "edge effects" still generate harmonic distortion components of high order and level, more impacting at lower levels. These latter aspects are decisive here on the effects on perception, which in common experience do not contribute to listening pleasure if they are not appropriately contained in the design phase.
Hard-clipping distortion analysis
Let's analyze the distortions introduced by hard-clipping, that is, an abrupt limitation of the signal when the values exceed a set threshold. These are typical distortions of solid state amplifiers when they come out of the normal working area. The transfer curve is shown in Figure 33 (top right), where the threshold is placed at a unit value. Here too it is not represented by a polynomial, but still a continuous function of C^infinity class, with a very pronounced "elbow".
Fig. 33 - Hard-clipping Distortions - Transfer Function, Harmonic Distortions, Time behaviour.
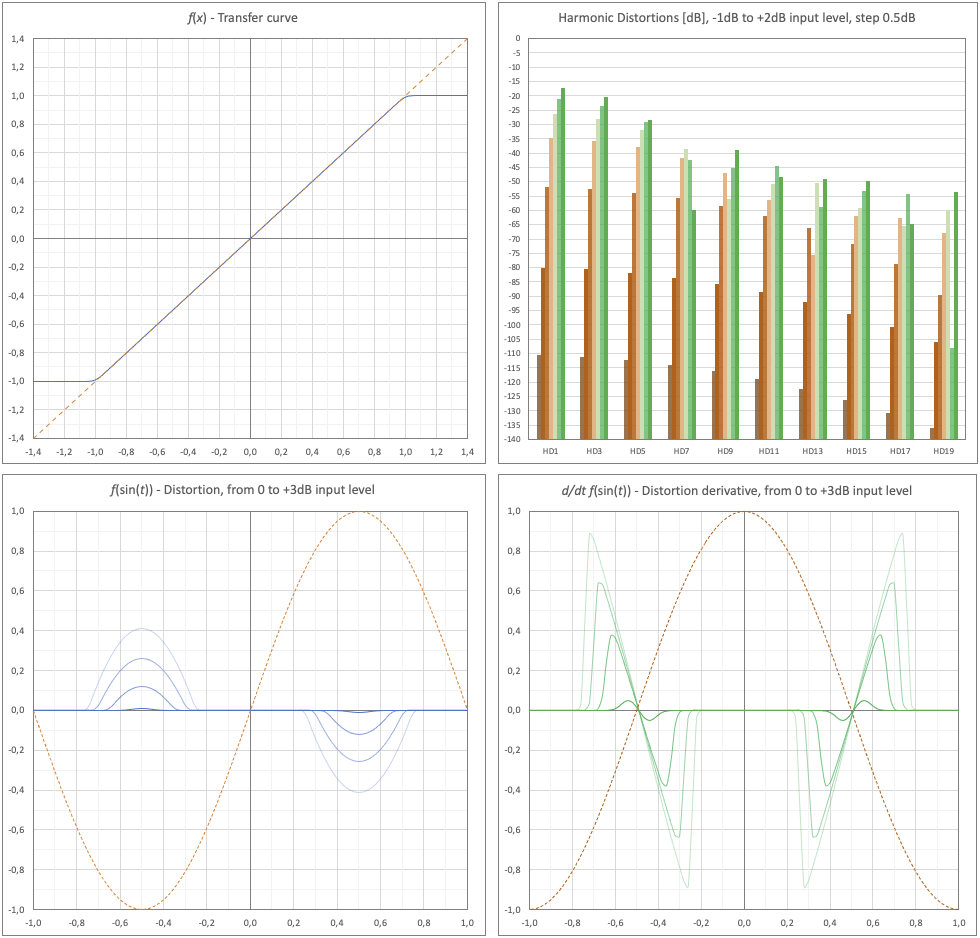
Applied to a pure tone we have, in the other graphs:
- Bottom left: distortion trend as the input level increases, from 0dB where the clipping effect is almost zero, to +3dB where the signal exceeds the clipping threshold by 1.4 times and therefore the cutting effect is more full-bodied. It is evident how the distortion takes the form of the upper (and lower) part of the sine wave where the threshold is exceeded, in phase opposition and which becomes wider as the input level increases.
- Bottom right: Derivative of distortion. Here, too, we note the ‘edge’ effect, that is, abrupt variations in the derivative at the signal transition from the cut to the unaltered zone, and vice versa. Therefore, we expect the generation of high-order harmonic distortions.
- Top right: The trend of harmonic distortions in absolute value as the input signal level changes, from -1dB to +2dB in steps from 0.5dB. Given the symmetry of distortion, only odd harmonics are present, including a contribution to the fundamental (HD1). As the signal level increases, harmonic distortions increase consistently for both the level and the order. At the limit, the distortion ‘tends’ to the original signal in counterphase.
For a music-like signal things are a bit different, given the different statistical distribution of signal levels, as in the case of crossover distortion. Here are relevant the high values of the signal, assumed less frequently by a real signal than a simple tone, as already shown in Fig. 7a. We have the following charts for transients.
Fig. 34 - PSD, PCD and DSA for hard-clipping distortion.
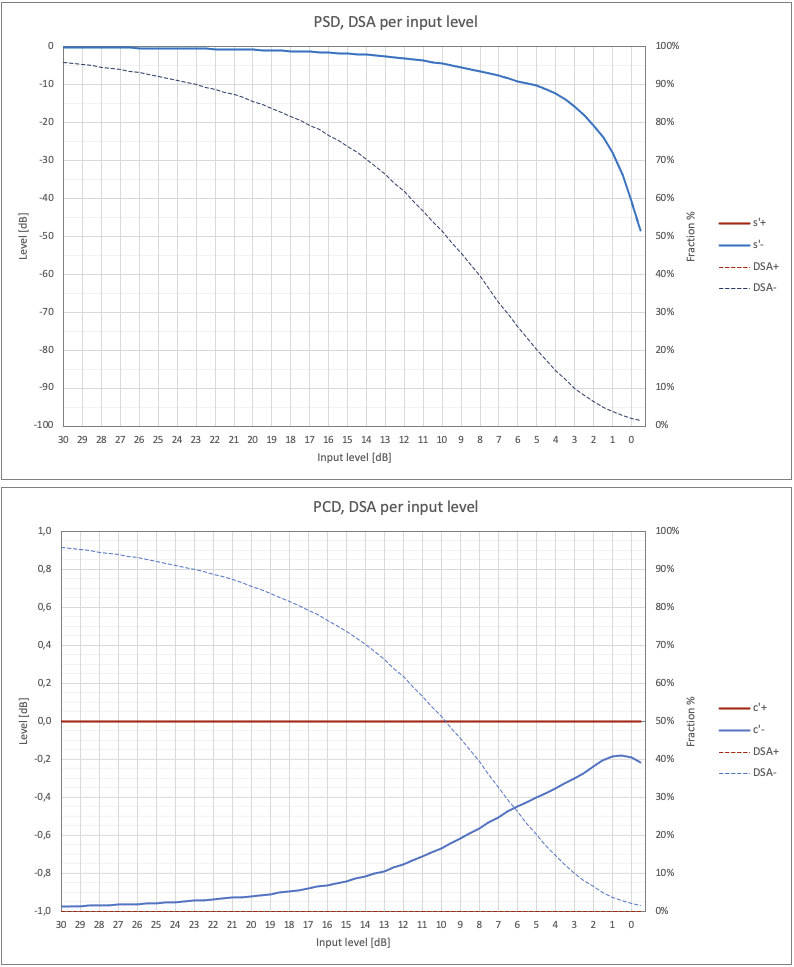
Here too, the sum of DSA+ and DSA- does not give 100%: the missing part is relative to the part of the signal whose transients are not altered, below the threshold value. Then, PSD and PCD will describe the behavior of distortion transients where the signal is above the threshold. We have:
- The fraction of expanded transients (DSA+) is identically null and therefore PSD+ and PCD+ will also be null.
- The fraction of compressed transients (DSA-) starts from values close to 0 for low signal levels (on the right) to increase progressively as the signal level increases, where ever wider parts of the signal are above the threshold. Here too, the DSA- actually represents the fraction of the signal above (in absolute value) of the clipping threshold.
- When the DSA- increases, the energy associated with compressed transients (PSD-) increases in value, tending to the original signal (0dB) in phase opposition.
- The negative correlation (PCD-) reflects the progressive similarity to the original signal as the DSA- increases.
From what we have seen, this distortion is dual to that of crossover: while for this the distortion is equal to the signal in phase opposition below a certain value (gap), for the hard-clipping the opposite occurs, that is, the distortion is equal to the opposite of the signal for values exceeding the threshold. There is also nothing new to the hard-clipping distortion: it is more relevant to the effects on perception the presence of harmonics of high order as the clipping increases compared to the impacts on transients.
Last edited:




