Introduction
In the engineering of electronic devices for music production or reproduction all designers are faced with the problem of minimizing the different forms of distortion inexorably introduced by their creations on the audio signal. They are commonly classified into two categories: linear and nonlinear. With reference to the representation of the signal in the frequency domain, the former are characterized by alterations of the modulus and phase of the signals; the latter instead add new frequency components due to the non-linear interaction of the frequencies present in the original signal. Both forms of distortion are often created voluntarily in production to give particular characters to voices or musical instruments, or to manage loudness and dynamics. Conversely, in playback, when of quality, both should be avoided, especially the nonlinear ones, given that the effects they cause on our perception could be not very "euphonic", non-reversible and are still being studied today. However, it should be noted that some audiophiles prefer, sometimes unconsciously, to use preamplifiers or power amplifiers which introduce some types of nonlinear distortions. More specifically, common experience shows that modest amounts of low-order non-linear distortion give the sound properties such as:
- 2nd order distortion: “warmer” and “softer” sound;
- 3rd order distortion: sound with more “dynamic contrast”.
These harmonics are musically “consonant”, i.e. they enrich the harmonic content of the sound, making it fuller. Involving perceptive aspects, the extent of these effects is subjective, depends on the musical content, as well as on the context, and is difficult to quantify. However, it should be noted that from the classic measurements performed on audio devices it is not so easy to deduce the aspects that are directly related to the aspects described. The aim of this study is to deepen the physical effects of nonlinear distortions on the signals to simplify the correlation with effects described on perception. Beyond the measurements and (non-formal) listening tests performed to support what will be explained, computer simulations of the behavior of some families of nonlinear systems were used as the main research tool. In these simulations both the classic test signals, such as pure tones and pulses, and multi-tone signals with characteristics analogous to musical ones were used. The final result will be the definition of numerical indicators useful for carrying out qualitative speculations with effects on perception and therefore helping designers to better understand how their own creation will behave.
Nonlinear distortion measurement
The commonly adopted approach to measuring non linear distortions on audio devices such as an amplifier is to assume that this is linear and permanent, and then look for deviations from this ideal model. In essence, the overall energy of the tones generated by our device on the output signal is measured against single or multiple tones at the input (a tone is a sinusoidal signal at a fixed frequency f). In the first case we will detect new harmonic components, i.e. new tones at multiple frequencies of the fundamental: 2f, 3f, 4f etc. In the second case we will also have intermodulation products, i.e. new tones resulting from the non-linear interaction of the tones present in the original signal. The new tones are generally at non harmonic frequencies: in the classic tests (CCIF and SMPTE), where only two tones are used at frequencies f1 and f2, we will have contributions at frequencies nf1±mf2, with n and m positive integers and whose sum is the intermodulation order. We numerically quantify the extent of the distortions with the indicators:
- THD (Total Harmonic Distortion): ratio between the RMS (Root Mean Square) value of the overall harmonic distortions and the RMS value of the tones in the original signal.
- IMD (InterModulation Distortion): ratio between the RMS value of the overall intermodulation products and the RMS value of the tones in the original signal. It should be noted that in some measurement standards such as CCIF and SMPTE, for simplicity of calculation, some of the lowest entity tones are neglected in the calculation.
The tones of the original signal to be considered in the calculation are those detected at the output of our device, which therefore also take into account its possible gain. Of the THD there is also the THD+N variant, which includes the noise component in addition to the distortion; its reciprocal is called SINAD (SIgnal to Noise And Distortion). It should be added that the measurements of the non linear distortion are strongly dependent on the spectral content and level of the test signal: it is therefore useful to detect the THD or IMD values on the audible frequency spectrum and for different levels of the input signal.
Criticisms have been raised in the literature of the THD and IMD indicators as being too simple to be representative of the amount of distortion experienced by an actual musical signal. To bring the measurements closer to the real world, multitone test signals can be adopted, where we will have a proliferation of harmonic distortions and above all of intermodulation products, which together form a sort of "carpet". Since it is very complex to separate them, the indicator that is used for this signal, the TD+N, does not distinguish them:
Criticisms have been raised in the literature of the THD and IMD indicators as being too simple to be representative of the amount of distortion experienced by an actual musical signal. To bring the measurements closer to the real world, multitone test signals can be adopted, where we will have a proliferation of harmonic distortions and above all of intermodulation products, which together form a sort of "carpet". Since it is very complex to separate them, the indicator that is used for this signal, the TD+N, does not distinguish them:
- TD+N (Total Distortion+Noise): Ratio between the RMS value of all distortions (including any noise) and the RMS value of all tones in the original signal.
For real example, on top of in figure 1 it is shown the distortions introduced by a real tube preamp (6H30 in a Mu-follower stage) for a 1KHz sinusoidal signal.
Fig. 1 - Measure of non-linear distortions: Two tones @19KHz+20KHz (CCIF test, top) and a single tone of at 1KHz (bottom).
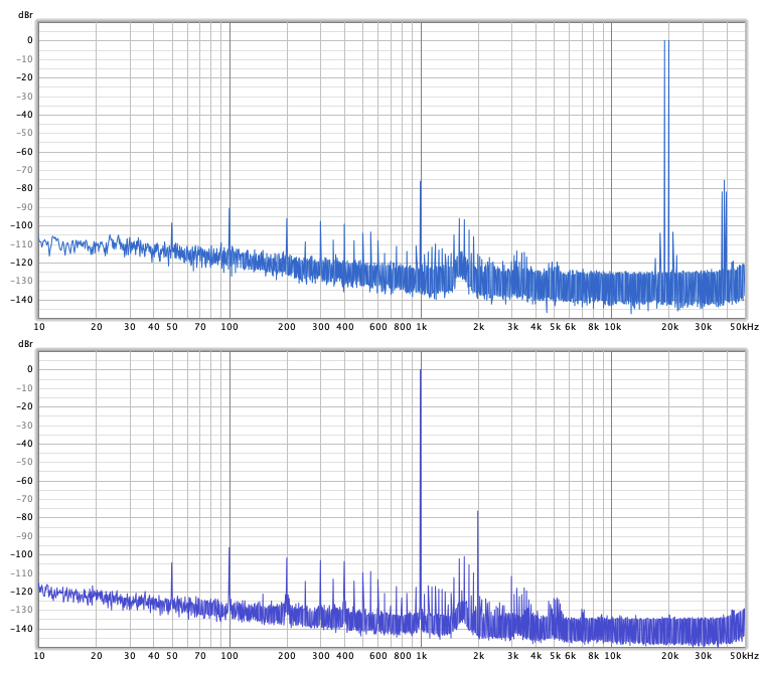
The 2nd order harmonic level is here of -76.6dB@2KHz while that of 3rd is very small, -112dB@3KHz; the THD detected is -72dB. The higher orders all have a lower level and not detectable here; the other tones present at lower frequencies are signal independent and are due to power supply. With two tones at 19KHz and 20KHz in a 1: ratio (CCIF test), below in the same figure, we see the intermodulation products, at 1KHz and in the side bands. The detected IMD is -76dB.
Listening experiences of this preamp reveal soft sound, with a slight emphasis on mid-low frequencies and a modest soundstage, at least when compared to a neutral solid state preamplifier like the Threshold FET Ten/e used as a reference. Which is in line with common experiences on the perception of distortions, as the preamp has predominantly 2nd order distortions. Now, none of the measurements or parameters listed provide clear clues to physical alterations on the signal that can be related to this perceived character for 2nd-order distortion, different from that of the 3rd. So let's try to understand what may be the determining aspects hidden in the measurements made.
Listening experiences of this preamp reveal soft sound, with a slight emphasis on mid-low frequencies and a modest soundstage, at least when compared to a neutral solid state preamplifier like the Threshold FET Ten/e used as a reference. Which is in line with common experiences on the perception of distortions, as the preamp has predominantly 2nd order distortions. Now, none of the measurements or parameters listed provide clear clues to physical alterations on the signal that can be related to this perceived character for 2nd-order distortion, different from that of the 3rd. So let's try to understand what may be the determining aspects hidden in the measurements made.
Model of nonlinearity
One way to study in detail the effects of nonlinear distortions is to mathematically model the input/output behavior of amplifiers for these aspects. We will then be able to build a simulator (a program) that replicates its behavior for any input signal and thus perform all our investigations on any type of signal.
The approach for the definition of the model is of the gray-box type, which means that it is based both on the observation of the input/output behavior of the system and on the partial knowledge of its internal structure. The construction of the model begins with identifying the cause that underlies the generation of non-linear distortion in amplifiers: the inconsistency of the gain for each input signal level. In other words, the input/output transfer curve f(x) is not a straight line in the working range but has "imperfections" around 0 or towards the extremes. By modeling this curve and calculating the output values for each value of the input signal, a simulator of our non-linear system can be obtained. This simple approach determines a static type model, for which the value of the output signal depends only on the instantaneous value of the input signal. In real amplifiers there is instead a dependence also on the values assumed in the past: it is said that the nonlinear system is “with memory” and the relative model, much more complex, is of the dynamic type.
In the study described we will adopt the static model, from which we will derive some effects of a general nature. Furthermore, the model is a good approximation of the behavior of amplifiers with limited memory effects in the working area. This family can be recognized by the following characteristics:
The approach for the definition of the model is of the gray-box type, which means that it is based both on the observation of the input/output behavior of the system and on the partial knowledge of its internal structure. The construction of the model begins with identifying the cause that underlies the generation of non-linear distortion in amplifiers: the inconsistency of the gain for each input signal level. In other words, the input/output transfer curve f(x) is not a straight line in the working range but has "imperfections" around 0 or towards the extremes. By modeling this curve and calculating the output values for each value of the input signal, a simulator of our non-linear system can be obtained. This simple approach determines a static type model, for which the value of the output signal depends only on the instantaneous value of the input signal. In real amplifiers there is instead a dependence also on the values assumed in the past: it is said that the nonlinear system is “with memory” and the relative model, much more complex, is of the dynamic type.
In the study described we will adopt the static model, from which we will derive some effects of a general nature. Furthermore, the model is a good approximation of the behavior of amplifiers with limited memory effects in the working area. This family can be recognized by the following characteristics:
- Flat frequency response, with extension at least up to 80KHz.
- Low level of harmonic distortions (< 3%) and frequency independence in the audio band.
- Phases of harmonic distortions independent of both frequency (always in audio band) and signal level.
In these hypotheses we will be able to model the transfer function f(x) by means of a polynomial. If the distortions we are interested in modeling are only of the 2nd and 3rd order we can limit ourselves to considering polynomials of the third degree:
In fact, by inserting a simple sinusoidal signal (x(t) = sin(ωt)) into this polynomial we will have that the different addends "control":
- a0 : component in DC, normally null.
- a1x : amplification (gain g) of the fundamental component.
- a2x²: 2nd order distortion, consisting of two components:
- 2nd harmonic (HD2), phase shifted by -90 degrees if a2 > 0; by +90 degrees if a2 < 0.
- DC, of the same entity as HD2.
- a3x³: 3rd order distortion, consisting of two components:
- 3rd harmonic (HD3), phase shifted by 180 degrees if a3 > 0; by 0 degree if a3 < 0.
- contribution to the fundamental component (HD1), 10dB higher than HD3.
Therefore, it is appropriate to distinguish the distortion of order i due to the i-th power addition of the transfer function, from the harmonic component of order i. In formulas, the first is represented by the i-th power by the function sin(ωt) and the second by the harmonic sin(iωt). We also recall that the phase shift of the harmonic sin(iωt) with respect to the fundamental sin(ωt) is given by the difference φi – iφ1, where φi is the phase of the i-th harmonic.
The block diagram used for the discrete simulation of a non linear preamplifier is shown in the following figure.
The block diagram used for the discrete simulation of a non linear preamplifier is shown in the following figure.
Fig. 2 - Simulator block diagram.
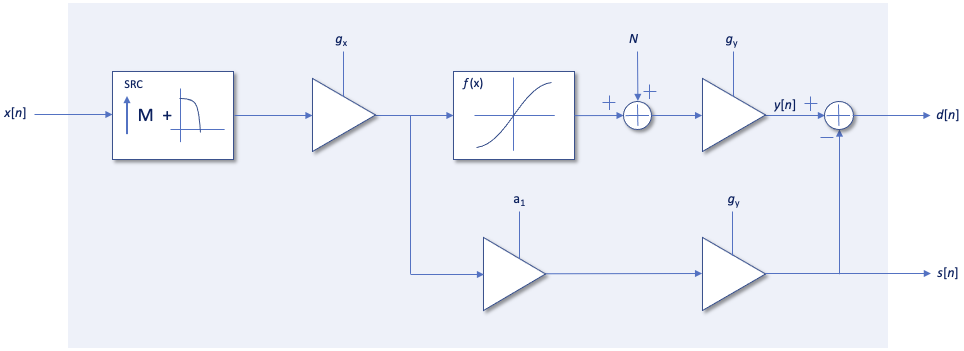
The discrete input signal x[m] is subjected to the following operations in cascade (main chain in the center):
- Upsampling of x[m] by an integer factor M, so that all subsequent processing works with a signal at a sampling frequency of at least 4 times the original and at 64bit. This is for reasons of precision in the calculations and to avoid potential aliasing phenomena due to the subsequent application of the nonlinear transfer function f(x).
- Attenuation of the 1/gx value, which simulates the input volume control.
- Application of the non linear distortion curve f(x), of gain a1. Optionally we can apply the complementary function g(x) in place of f(x) such as to cancel the effect of f(x), i.e. g(f(x)) = x.
- Addition of Gaussian white noise N[n] to simulate the contribution of thermal noise.
- Attenuation of the 1/gy value, which simulates the output volume control (alternative to input attenuation).
Each operation can be configured and excluded. The resulting signal, y[n], represents the distorted signal. For subsequent statistical analyses, y[n] must be separated into two parts: only the distortion component d[n] and the reference signal s[n] not subject to non linear distortions. This signal is obtained in the lower chain by applying to the upsampled input signal x[n] the overall linear amplification (gx, a1 and gy). The signal d[n] is therefore obtained by subtracting s[n] from y[n].
In order to focus on the main concepts of the study, in addition to the assumptions already exposed, in the following simulations we will make the following simplifying assumptions:
In order to focus on the main concepts of the study, in addition to the assumptions already exposed, in the following simulations we will make the following simplifying assumptions:
- Absence of bandwidth limitation, equivalent to considering the system with a cutoff frequency response much higher (at least 4 times) than the maximum frequency contained in the input signal.
- Negligible noise (null N[n]).
- Attenuation and unity gains (gx = a1 = gy = 1).
With these hypotheses, the input signal x[m] and the output signal s[n] coincide. The preamplifier described in the previous paragraph (moreover, without feedback) is well represented by this model. As a check we can generate test signals and compare the amplifier output with that of the simulator. As a sample, the graph in figure 4a shows the preamplifier output for a series of 8 tones equally spaced in frequency from 10KHz to 17KHz, level at -18dB and fs = 192KHz. In the graph, the intermodulation products in the sidebands of the original tones are clearly seen. The second diagram shows the result of the simulator for the same source signal with a 2nd and 3rd order distortion level obtained from measurements with single tones, together with the ‘noise carpet’, distinguishing the undistorted signal s[n] in red from the distortion component d[n] in green.
Fig. 3 - Measure (top) and Simulation (below) with 8 tones @ 10KHz, 11KHz, …, 17KHz; input at 1Vrms; 0dB Gain.
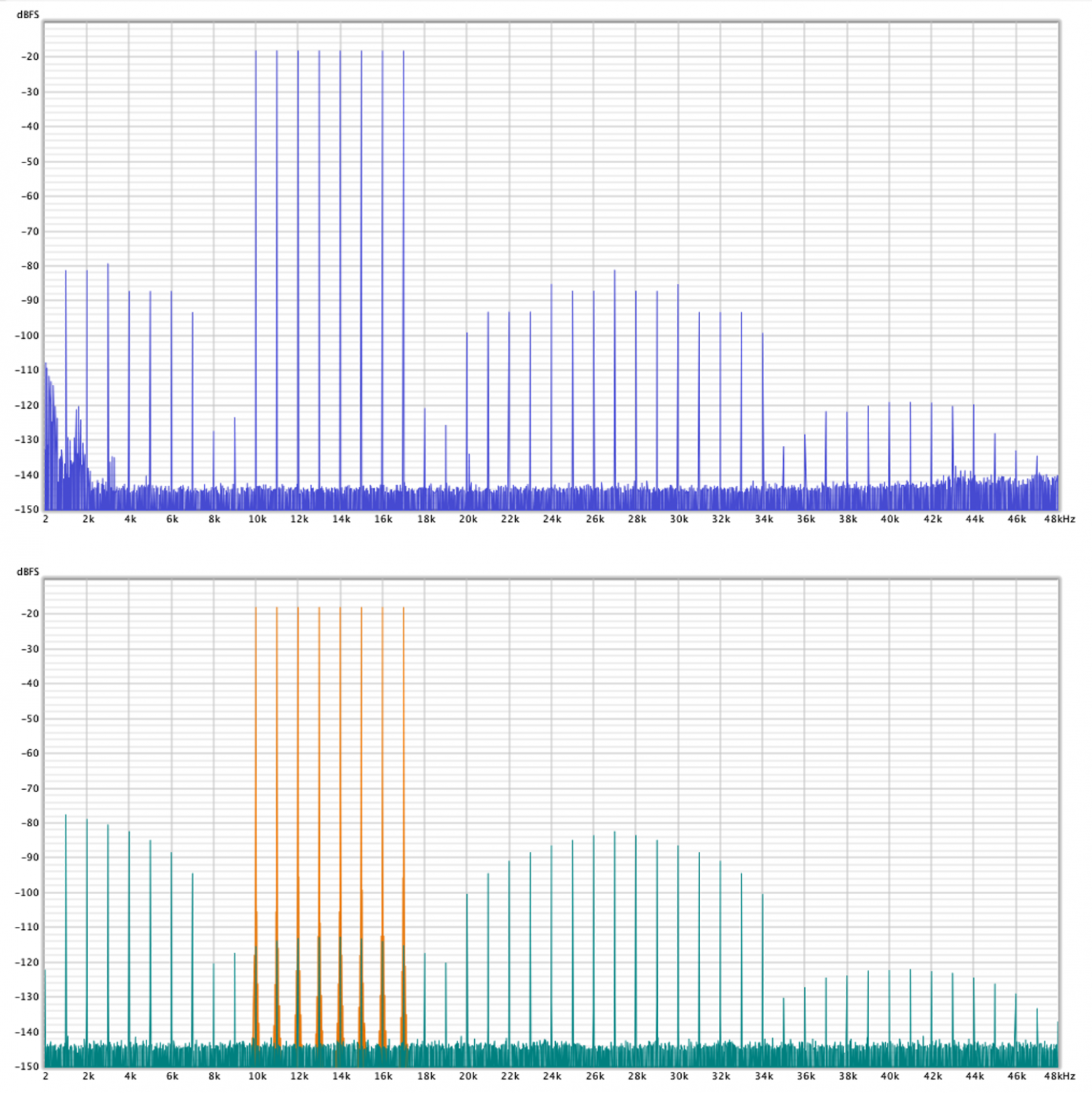
The agreement is very good; the small differences are due to neglecting linear distortions (the frequency response of the preamp not perfect for module and phase) and interactions with the nonlinear distortions of the DAC/ADC converters of the measuring instrument. Note the distortion components coinciding with the original tones, not detectable in the measurements, which we will return to later. It should be pointed out also that the use of y[n] in listening tests to simulate the distortions of a real amplifier should be taken with precautions, the details on this post.
Elements of psychoacoustics
To understand why the analysis of the alterations undergone by the signals will be oriented in the directions that we will see, it is necessary to mention some aspects of psychoacoustics. In a nutshell, the transduction of vibrational energy into electrical signals to the brain is performed by the cochlea, which acts as a sort of spectral analyzer, decomposing complex signals into simpler elements. This operation is performed by the hair cells, whose precision is exceptional. At the limits of hearing, these can detect movements caused by sound at infinitesimal levels and respond within a few microseconds. Furthermore, they can quickly adapt to constant stimuli, thus allowing the brain to extract both localization information of sounds and their tonal structures, even in the presence of a lot of background noise.
To better understand how these mechanisms operate, we can temporally divide a real signal into two parts: the first, called transient, which in turn consists of an "attack" part (about 1ms) followed by a second (variable between 10ms and 30ms) that we can call "settlement". The second, in the steady-state, in which the sound becomes almost stationary and then dies out. Even if in the literature there is not much clarity on the identification of the parts of a sound which are part of the transient and which of the steady-state, our phenomenal auditory system uses the former to determine the localization of the sound source, i.e. its position in the space and its dimension; the second to identify pitch and timbre. The latter are detected by decomposing the sound into its spectral components in the range 20Hz-20KHz (well 10 octaves) in a similar way to Fourier analysis, but with several differences. In summary, when the ear is stimulated by a single tone, impulses are generated towards our brain which identify a range of frequencies around this tone, more extensive towards the high frequencies than the low ones, which inhibit the detection of other lower tones in this range. These intervals oscillate between 1/3 and 1/6 octave and are called “critical bands”. Tones that fall in the same or different bands will cause different stimuli. The masking effect which depends on the signal level, but also on the relative phase between the tones involved, and also occurs when the signals are separated in time. For pitch and timbre we are mainly sensitive to tone levels; the dependence on the phases is marginal, but becomes more important if they vary over time.
Sound localization occurs through two mechanisms, which depend on the frequencies present in the signal. For frequencies lower than 1.5KHz, the temporal differences (ITD) between the sounds reaching the ears are detected, whose phase is "locked" with precision. For higher frequencies this mechanism (effective than in owls up to 9KHz), gives way to the analysis of the difference in signal levels (ILD). In fact, for sounds over 2KHz, the human head behave like an acoustic obstacle, given the small wavelength of the sound compared to it. Several studies have shown that the temporal sensitivity is very high, between 6μs and 10μs, which determine a spatial accuracy of about 1 degree.
These two mechanisms work simultaneously and, although the above is a simplification, they allow us to more easily classify the impacts on perception caused by changes in sound. Consistent alterations of the transient part can cause more "fatigue" to our brain in resolving spatial aspects, with consequent degradation of localization aspects; alterations in the frequency content will have an impact on the timbre and pitch of the sound. Given the masking effects, the non-harmonic distortions (IMD) are more decisive for the latter, which occur at frequencies far from the original ones and therefore potentially more audible.
To better understand how these mechanisms operate, we can temporally divide a real signal into two parts: the first, called transient, which in turn consists of an "attack" part (about 1ms) followed by a second (variable between 10ms and 30ms) that we can call "settlement". The second, in the steady-state, in which the sound becomes almost stationary and then dies out. Even if in the literature there is not much clarity on the identification of the parts of a sound which are part of the transient and which of the steady-state, our phenomenal auditory system uses the former to determine the localization of the sound source, i.e. its position in the space and its dimension; the second to identify pitch and timbre. The latter are detected by decomposing the sound into its spectral components in the range 20Hz-20KHz (well 10 octaves) in a similar way to Fourier analysis, but with several differences. In summary, when the ear is stimulated by a single tone, impulses are generated towards our brain which identify a range of frequencies around this tone, more extensive towards the high frequencies than the low ones, which inhibit the detection of other lower tones in this range. These intervals oscillate between 1/3 and 1/6 octave and are called “critical bands”. Tones that fall in the same or different bands will cause different stimuli. The masking effect which depends on the signal level, but also on the relative phase between the tones involved, and also occurs when the signals are separated in time. For pitch and timbre we are mainly sensitive to tone levels; the dependence on the phases is marginal, but becomes more important if they vary over time.
Sound localization occurs through two mechanisms, which depend on the frequencies present in the signal. For frequencies lower than 1.5KHz, the temporal differences (ITD) between the sounds reaching the ears are detected, whose phase is "locked" with precision. For higher frequencies this mechanism (effective than in owls up to 9KHz), gives way to the analysis of the difference in signal levels (ILD). In fact, for sounds over 2KHz, the human head behave like an acoustic obstacle, given the small wavelength of the sound compared to it. Several studies have shown that the temporal sensitivity is very high, between 6μs and 10μs, which determine a spatial accuracy of about 1 degree.
These two mechanisms work simultaneously and, although the above is a simplification, they allow us to more easily classify the impacts on perception caused by changes in sound. Consistent alterations of the transient part can cause more "fatigue" to our brain in resolving spatial aspects, with consequent degradation of localization aspects; alterations in the frequency content will have an impact on the timbre and pitch of the sound. Given the masking effects, the non-harmonic distortions (IMD) are more decisive for the latter, which occur at frequencies far from the original ones and therefore potentially more audible.
Time analysis of sinusoidal and impulsive signals for single order distortions
Let's start by analyzing the shape of the distortions in the time domain related to transfer curves that have only one of the two orders, 2nd or 3rd. Furthermore, we will assume for now that the coefficients ai are all non negative; it is not a very realistic situation, but it allows us to understand how the two orders act separately on the signal.
The first two graphs at the top of Figure 4 show these transfer curves in the normalized working range [-1, +1], with a0 = 0 (DC) and a1 = 1 (unit gain); the one on the left with only HD2 = -60 (a2 positive, equal to 0.002) and the one on the right with only HD3 = -60dB (a3 positive, equal to 0.004). For both, the THD is equal to 0.1%. The curves are amplified by 100 times with respect to the 45 degree straight line to show its trend.
The first two graphs at the top of Figure 4 show these transfer curves in the normalized working range [-1, +1], with a0 = 0 (DC) and a1 = 1 (unit gain); the one on the left with only HD2 = -60 (a2 positive, equal to 0.002) and the one on the right with only HD3 = -60dB (a3 positive, equal to 0.004). For both, the THD is equal to 0.1%. The curves are amplified by 100 times with respect to the 45 degree straight line to show its trend.
Fig. 4 - Source signal (top) and its 2nd order (middle) and 3rd order (bottom) distortions, last two amplified. Detail, Time simulation.
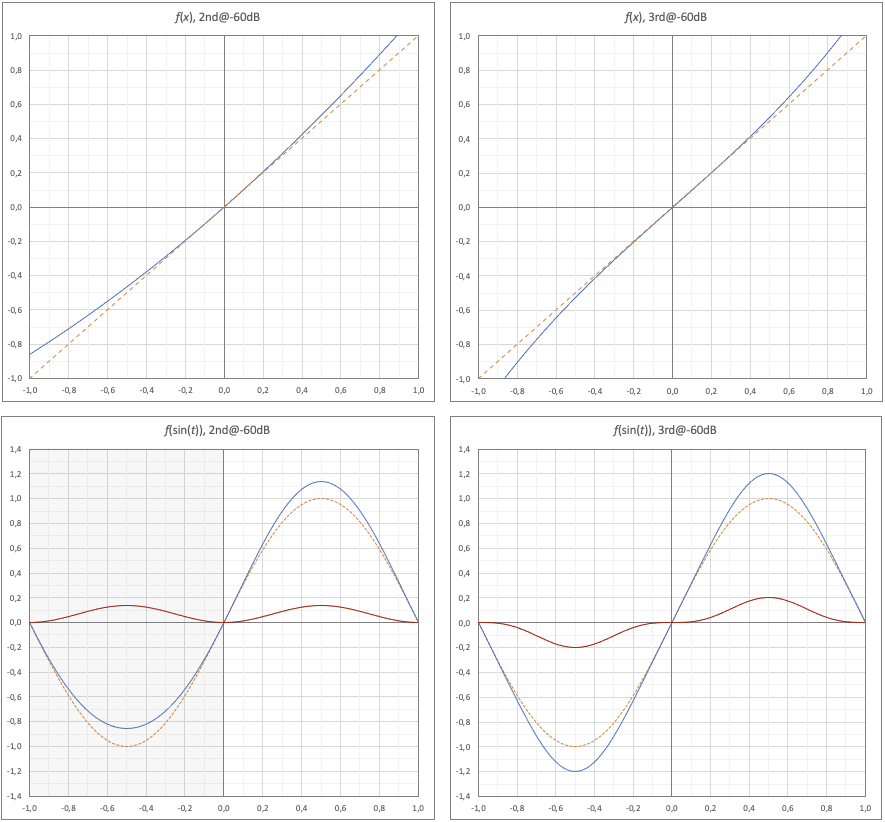
The lower part shows the deformation undergone by the classic sine wave: the source curve in orange; in blue the distorted curve and in red the distortion alone, always amplified by 100 times. The transfer functions act on the signal as follows:
- 2nd order: Expansion of the positive values of signal (f(x)>x for x>0) and compression of the negative ones (f(x)<x for x<0); the distortion is asymmetrical.
- 3rd order: Expansion of both positive and negative values of signal (|f(x)|>|x| for |x|>0); the distortion is symmetrical.
We now use the simulator to study more complex signals: we build a source signal composed of several equally spaced tones in frequency at the same level and phase: 100 tones spaced 200Hz from each other, from 50Hz to 20KHz, level at -40dB to avoid clipping; for the phase we choose the same constant value, for example -90 degrees, to move the signal more. In the time domain all these tones are constructively summed up in a few short time windows: the signal takes the form of a sinc pulse train, given the band limitation at 20KHz, with alternating phases of 0, -90, -180 , -270, 0, ... degrees, and spaced 1/200 sec.
Let us now simulate the passage of this signal through two static nonlinear systems which have the same distortions of figure 5. Figure 6 shows the detail for a single pulse out of phase by -90 degrees in channel 1; channels 2 and 3 show only the resulting distortion components, both amplified by 50dB to highlight their trend. The signal is sampled with fs = 192KHz.
Let us now simulate the passage of this signal through two static nonlinear systems which have the same distortions of figure 5. Figure 6 shows the detail for a single pulse out of phase by -90 degrees in channel 1; channels 2 and 3 show only the resulting distortion components, both amplified by 50dB to highlight their trend. The signal is sampled with fs = 192KHz.
Fig. 5 - Source signal (top) and its 2nd order (middle) and 3rd order (bottom) distortions, last two amplified. Detail, Time simulation.
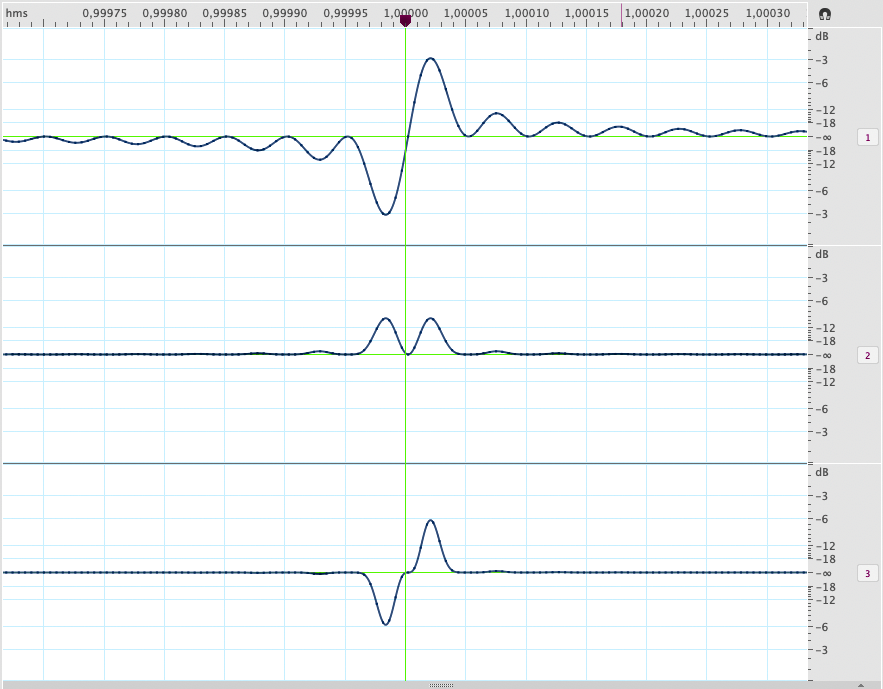
We observe that:
- 2nd order distortion always assumes positive values, proportional to the absolute value of the source signal, compressing the negative half-wave and expanding the positive half-wave (asymmetrical distortion). As a consequence we will have simultaneously effects of attenuation and enhancement of the transients.
- 3rd order distortion instead enhances both positive and negative half-waves, thus increasing the steepness of all transients; the signal extension also increases symmetrically.
Therefore, the expansive and compressive effects behave as in the simple sinusoidal case.
Time analysis of music-like signals for single order distortions
Let us now try to understand how much of the considerations in the previous paragraph apply to a signal more similar to a musical one. The "music-like" test signal is built in frequency synthesis with the following characteristics:
- 64 tones, from 30Hz to 48KHz, in 1/6 octave steps;
- initial level at -24dB, linearly decreasing in frequency at -2dB/KHz;
- random phases with uniform distribution in the range ±180 degrees.
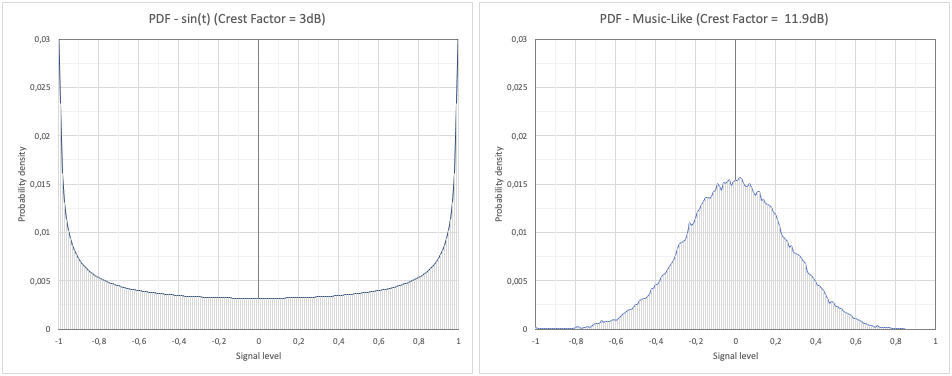
This signal will appear erratic over time, given the random phases and the relationships between the frequencies. The level distribution is of the Gaussian type with a crest factor of about 12dB (average value), consistent with that of a real musical signal; figure 6a shows the comparison of the distribution with that of a sinusoidal signal. The differences in level concentration are evident: the peak values are around 0 for the music-like signal; at the extremes for sinusoidal signals.
Fig. 6a - Probability Density Function (PDF). Left: sinusoidal signal; right: music-like signal.
The time trend is shown in Fig. 6b, together with the relative 2nd and 3rd order distortions, always at -60dB on a single tone, which follow its trend.
Fig. 6b - Source signal (top) and its 2nd order (middle) and 3rd order (bottom) distortions, last two amplified of 55dB.
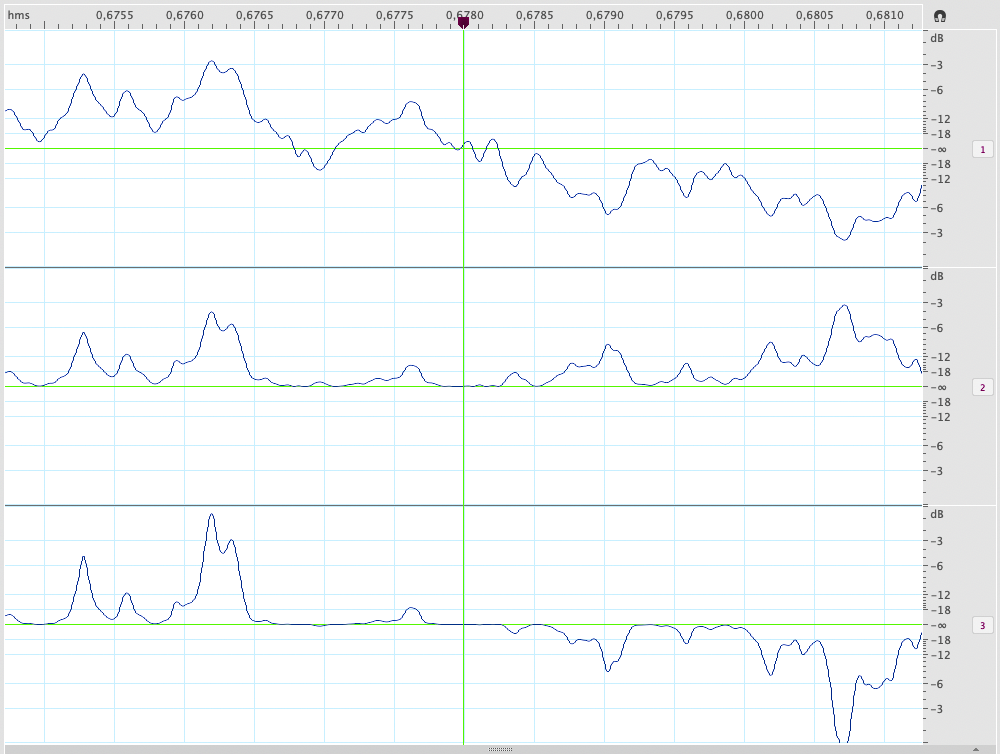
Upon visual inspection, both distortions seem to be attributable to the curves of Figure 5, applied to each micro-transient: here too the 3rd order distortion enhances all transients; that of 2nd enhances the transients where the signal is positive and attenuates the negative ones. At this point, it is appropriate to define statistical indicators that provide quantitative evidence, which can leverage the availability of the source signal and that of the distortion separately and aligned in time.
DSA: Derivative Sign Agreement
The first indicator, the DSA, characterizes the type of nonlinear alteration undergone by the transients, where by "type" we mean the two effects found, which we will call expansive and compressive. Mathematically, the DSA is expressed by the fraction of the overall agreement (or disagreement) between the transients of the source signal and those of the distortion. Transients are qualified through the derivative of each signal, which expresses the speed with which the signals vary, positive when the signal increases and negative when it decreases. So:
- Where there is agreement between the sign of the derivative of the source signal and that of the distortion we will have an increase or decrease in the speed of the transient; therefore, an expansive effect.
- Where there is discordance the distortion will reduce the speed and level reached of the transient; therefore, a compressive effect.
If we have upsampled the signal over time x4 or more, we can get a good approximation of the derivatives by simply calculating the difference between the consecutive pairs of samples at this higher frequency. Let's see what has been described with an example.
Fig. 7 – DSA Domains identification - Example.
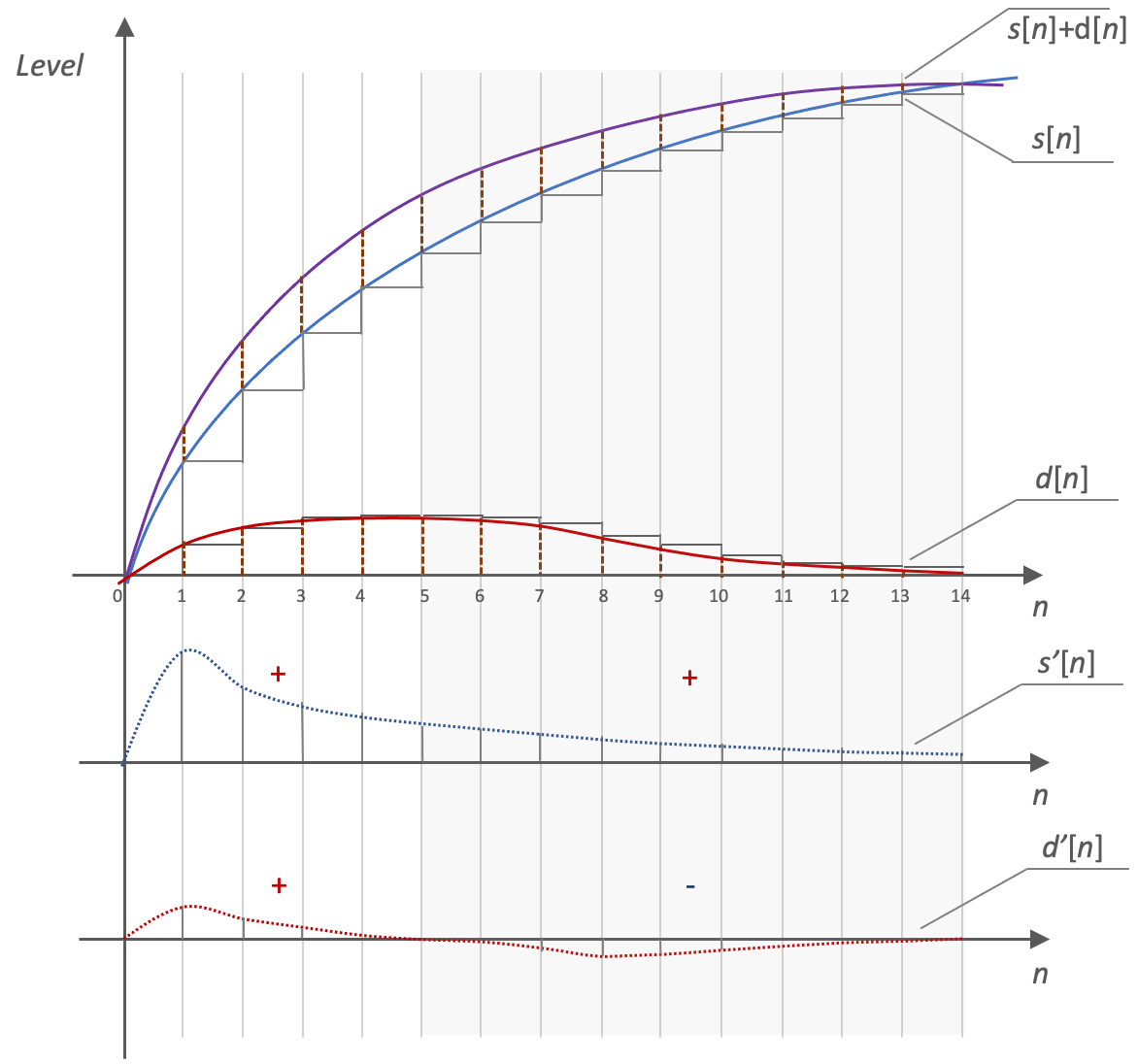
Figure 7 shows at top a segment of the original signal s[n] in blue ever-increasing; in purple the distorted signal s[n]+d[n] (heavy way to show the details). The difference between the two signals, in red, is therefore the distortion component d[n]: it grows fast in a first stretch and then decreases more slowly. In the center is shown the s'[n] derivative of the original signal that always assumes positive values, since s[n] is always increasing. At the bottom the derivative d'[n] of the distortion component: up to n=5 it is positive, like s’[n]: so the distortion increases the slope of s[n], as is evident in the curve in purple. Subsequently, d'[n] becomes negative, a sign opposite to s'[n], indicating that the distortion decreases the slope of s[n]. Here the transient agreement is 5/(5+9) = 0.36.
We will indicate in the following the set (domain) of the indices of the samples of the signal where there is expansion with '+' (positive); with '-' (negative) where there is compression. Unless explicitly specified, the positive transient domain is understood; the negative ones will be equal to 1 - DSA.
We will indicate in the following the set (domain) of the indices of the samples of the signal where there is expansion with '+' (positive); with '-' (negative) where there is compression. Unless explicitly specified, the positive transient domain is understood; the negative ones will be equal to 1 - DSA.
PSD: Partialized Signal Distortion
This second indicator actually consists of a family of indicators with which we quantify the non-linear distortion suffered by a signal for specific views. In essence, the definition of the TD+N indicator extends: given a reference signal x and a second y whose relative energy contribution we want to evaluate if added to x, the PSD is defined as the ratio between:
- the RMS value of y calculated on the signal values assumed in a domain identified by time or frequency intervals;
- the RMS value of the overall x signal.
- D is the entire time or frequency domain: with x[n] = s[n] and y[n] = d[n], we will have that the PSD will coincide with the classic value of the THD+N when the source signal is a single tone; with TD+N in case of multitone signals (actually in some cases there are discrepancies which will be explained later).
- If D is in frequency, and X[n] = DFT{s[n]}, Y[n] = DFT{d[n]}, with the PSD it is possible to quantify the distortion by frequency bands, for example by octaves or fractions thereof.
- If D is in time, and x[n] = s'[n] and y[n] = d'[n], with the PSD we can quantify:
- The distortion per level if we consider the signal levels s[n] as domains.
- The alteration of expanded or compressed transients if as domains we consider the positive or negative one identified by the DSA. For the sake of brevity, we will denote these two values s'+ and s'- below.
The choice of the derivatives of signals in the last point is necessary to cancel the effects of the deviations accumulated on the different levels or in any case the effect of deviations in DC. Of course, even for the PSD higher values (expressed in dB or as a percentage) imply higher distortion, which is therefore potentially more audible. Using a simulator where noise is not modeled, the PSD will only measure non linear distortion, and therefore will be equivalent to THD or TD+N, without “N”.
Returning to the signal in question, we will have:
⁃ 2nd order: DSA = 50%, s'+ = -59.9dB, s'- = -59.7dB TD+N = -63.1dBReturning to the signal in question, we will have:
⁃ 3rd order: DSA = 100%, s'- = -57.4dB, s'- = N.D. TD+N = -60.3dB
The DSA values confirm the visual inspection of the transients: both orders act on the micro-transients according to when seen for the impulsive signal (also here the DSA assumes the same values). PSD values tell us that the amount of distortion is slightly greater for the 3rd order.
Frequency analysis of music-like signals for single order distortions
To complete the picture we perform the analysis in the frequency domain. The following diagrams show the frequency trend of the signals in figure 6b. The spectrum of 2nd and 3rd order distortions, both at -60dB, are shown in figures 8b and 8c. The levels of these signals refer to the envelope of the source signal shown in orange in fig. 8a, decreasing in frequency to -2dB/KHz. The same figures also show a second distortion spectrum without the frequency components coinciding with those in the source signal: considering that this is composed of tones in harmonic ratio, this second spectrum highlights only the intermodulation products.
Fig. 8a - “Music-like” source signal (in blue) and its envelope (in orange).
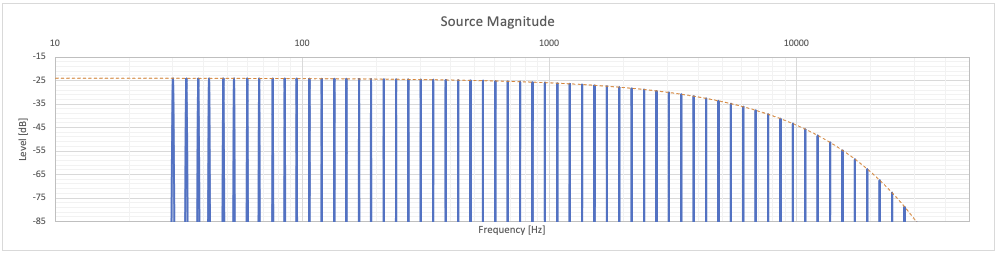
Fig. 8b - 2nd order distortion, -60dB, with (a) and without (b) source signal tones; ref. to its envelope.
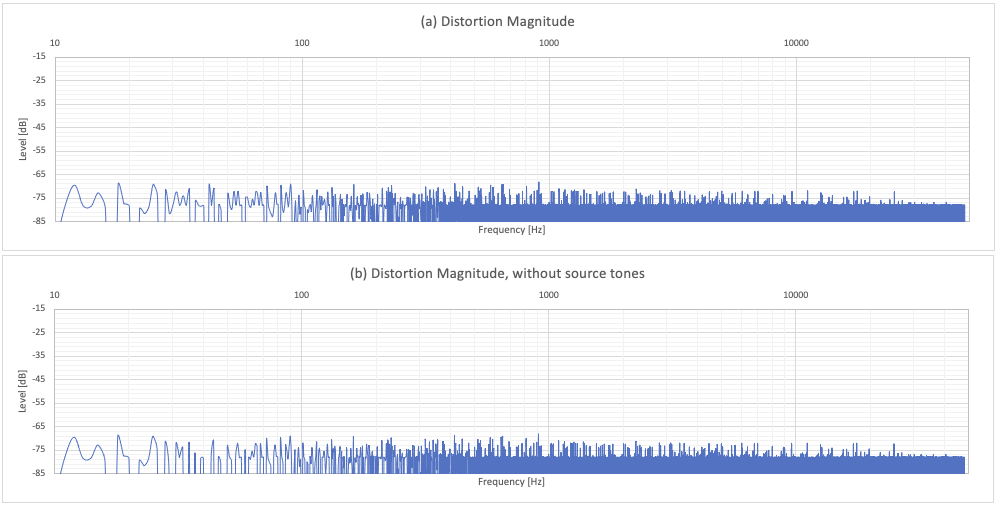
Fig. 8c - 3rd order distortion, -60dB, with (a) and without (b) source signal tones; ref. to its envelope.
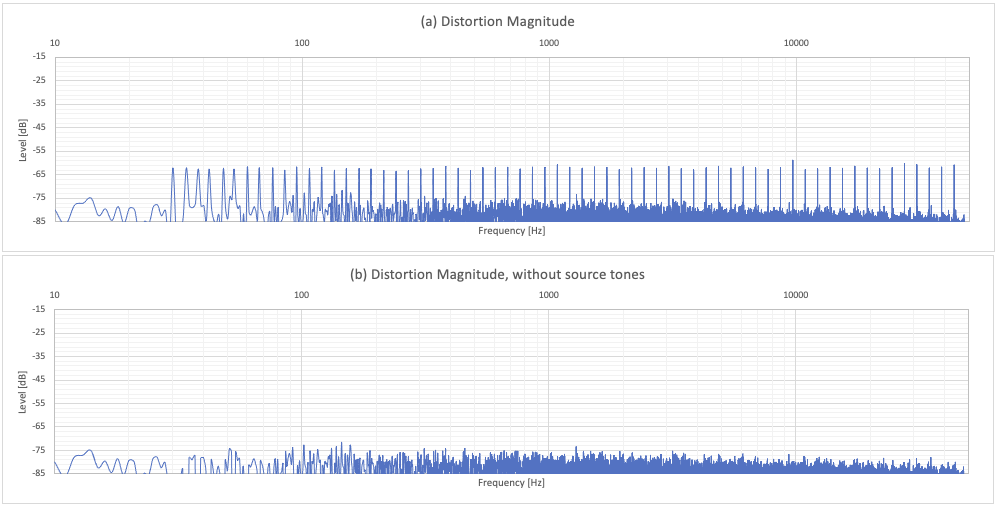
Fig. 8b - 2nd order distortion, -60dB, with (a) and without (b) source signal tones; ref. to its envelope.
Fig. 8c - 3rd order distortion, -60dB, with (a) and without (b) source signal tones; ref. to its envelope.
It is evident how the intermodulation products here determine a sort of "carpet" of distortion. For the 2nd order we have 3436 components; for the 3rd as many as 43108. As the order of distortions increases, the number of intermodulation products increases exponentially. On the qualitative trend of the distortions we can state that:
- The level of the distortion carpet, referred to the envelope of the source signal, is almost constant for both orders.
- The 2nd order distortion peaks are modest, "almost" random and constant in frequency, denser at low frequencies and generally not coinciding with the tones of the source signal.
- The 3rd order distortion peaks are very pronounced, almost at the same level and coinciding with the tones of the original signal (phase synchronized, not shown).
The last two points can be seen quantitatively in the following figure which reports the density of the source tones, of the distortions and therefore the PSD of the same signals per octave, with and without the distortion components at the same frequency as the tones in the source signal. Due to how the source signal is structured, this last value indicates the contribution of non harmonic intermodulation products.
Fig. 8d - Source signal density, 2nd and 3rd order distortions (top) each at -60dB and related PSD (bottom), per octave.
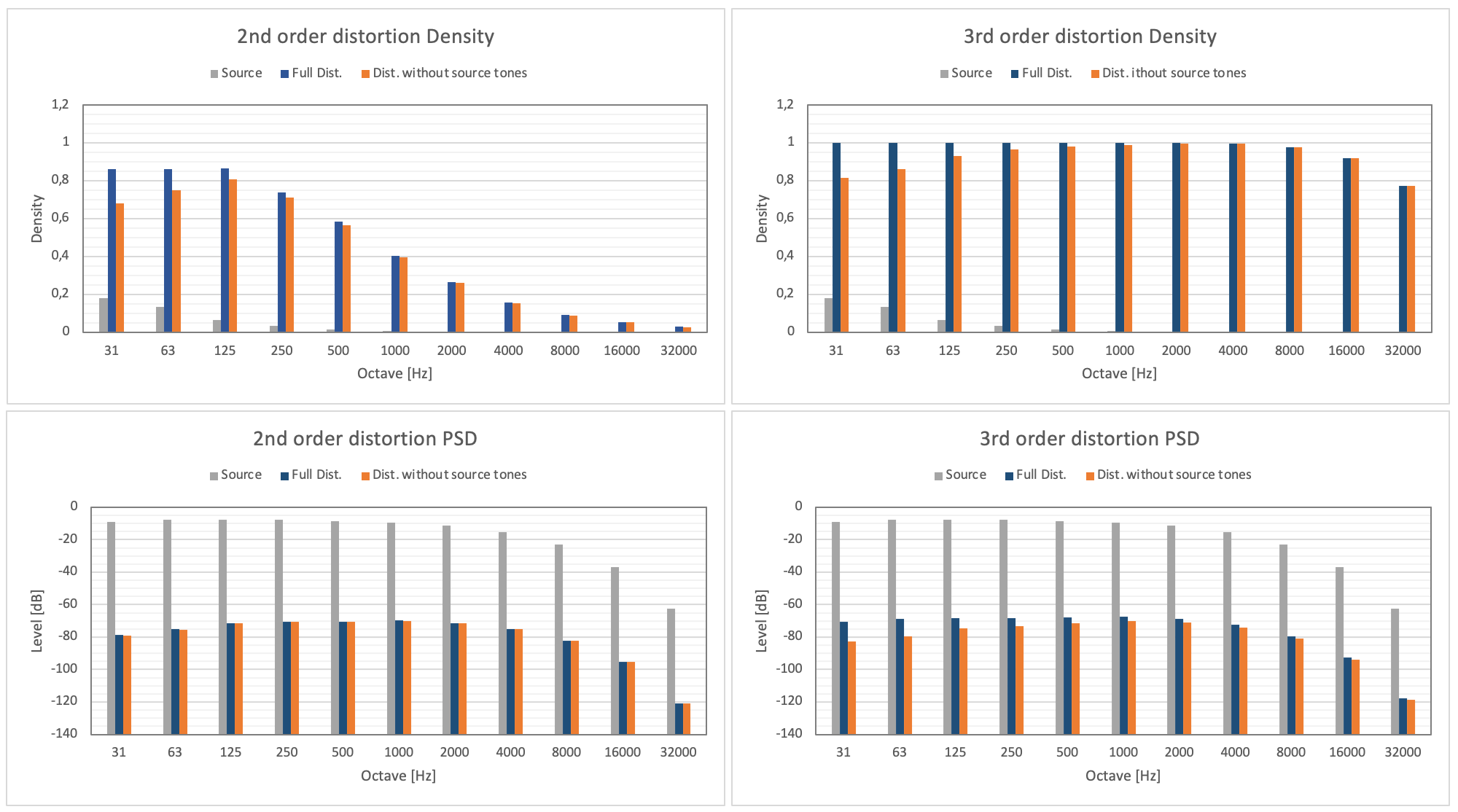
We have:- 2nd order: the density graph shows how there is a concentration of the number of intermodulation products in the lowest octaves. The RMS value (PSD) increases slightly for medium frequencies, to then drop more decisively in high frequency, following the tonal trend of the source signal. By eliminating the tones coinciding with those of the source signal, negligible variations are obtained.
- 3rd order: the density graph is almost constant for all octaves, while the PSD decreases only in the high frequency. Differently from the 2nd order, if here we eliminate the tones coinciding with those of the source signal we have a more consistent decrease (up to 12dB) of the low frequency intermodulation products.
It should be added that these considerations are derived from the analysis of the trends of the distortions on a hypothetical musical signal; carrying out other simulations with signals with different characteristics, a change is observed for the quantitative aspects, i.e. slope of the carpet, variations in the density of the peaks etc., but the behaviors described, in the working hypotheses set out, remain substantially unchanged.
Correlation between physical aspects and effects on perception
Given the physical characteristics of the distortions and the main psychoacoustic mechanisms, we can speculate on their correlation. We'll have:
- 2nd order (positive)
- Time: Expansion of positive transients and compression of negative ones. From listening experiences, there is a greater depth in the soundstage, probably due to the greater energy in the "attack" parts of the sound.
- Frequency: The 2nd harmonic is an octave above the fundamental frequency; It is therefore perfectly consonant with the original tone and a feeling of greater "fullness" to sound. Intermodulations are distributed in the form of a carpet, with a greater concentration in low frequency: this determines a "swelling" effect of the low frequencies.
- 3rd order (positive)
- Time: Expansion of both transients, positive and negative. The effect is similar to that of 2nd order distortion, even if of a different character, in terms of position and size, which are more clear-cut.
- Frequency: The 3rd harmonic is still harmonic (the octave of the fifth), and therefore still consonant with the original tone. So, this too “fills” the sound. The distortion carpet due to intermodulation is constant in frequency, with peaks coinciding with the frequencies of the tones in the source signal, in phase. This determines an effect of expansion of the micro and macro-dynamics.
Of course, the extent of these effects depends on the amount of distortion. If too small, there is no audible effect; if in excess, they result in sound-muddling, swelling, or harshness effects.
It is interesting to note an analogy with our visual system regarding transients. If we look at the 3rd order distortion curve in figure 5, we notice that this is attributable to the effect caused by the "unsharp mask" filter. This filter, due to Laplace, does nothing but detect the edges between the elements in an image, identified by the intensity gradients: by subtracting the result of this filter (possibly attenuated) from the original image, a sort of double edge is added to each element of the image, in which the darkest part is further darkened and the lightest part lightened. This effect is clearly visible at close range, but if we observe the image from a distance, our visual system perceives an effect of greater sharpness. The filter relating to the 2nd order, on the other hand, does not appear to be used. An example of applying these filters non-aggressively is in figure 9.
It is interesting to note an analogy with our visual system regarding transients. If we look at the 3rd order distortion curve in figure 5, we notice that this is attributable to the effect caused by the "unsharp mask" filter. This filter, due to Laplace, does nothing but detect the edges between the elements in an image, identified by the intensity gradients: by subtracting the result of this filter (possibly attenuated) from the original image, a sort of double edge is added to each element of the image, in which the darkest part is further darkened and the lightest part lightened. This effect is clearly visible at close range, but if we observe the image from a distance, our visual system perceives an effect of greater sharpness. The filter relating to the 2nd order, on the other hand, does not appear to be used. An example of applying these filters non-aggressively is in figure 9.
Fig. 9 - Left: 2nd order distortion simulation. Right: 3rd order. Top: original RAW image.
The image on the right, equivalent to the 3rd order, appears sharper, more "dynamic", enhancing both transients. In the image on the left, equivalent to the 2nd order, this effect is still present but less pronounced, appearing overall "softer". Both modified versions seem to improve on the original image: of course it's not the same processing that our auditory system does, but it seems a nice coincidence for the equivalent effect on sound!
Analysis of music-like signals with mix of 2nd and 3rd order distortion
Let's now analyze how DSA and PSD behave in more realistic situations where both orders of distortion are present. Let's start by setting a reference level for the 2nd harmonic and vary the level of the 3rd. We will briefly express this variation as the ratio between the 3rd/2nd levels in dB. Figure 10 shows two graphs; the first, as a reference for a single tone, reports the curves:
- The level of harmonics related to 2nd order distortion (in red) and 3rd order (in blue). For the 2nd order we have the 2nd harmonic (HD2) equal to the reference value set at -90dB (DC is omitted). For the 3rd order, we have two components: the 3rd harmonic (HD3) and the contribution to the fundamental frequency (HD1), which is always higher than 10dB. These increase progressively, from -48dB to + 48dB compared to the HD2 level.
- The True-THD (in purple), with which we indicate the value of the Total Harmonic Distortion in which we also consider the distortion of the fundamental (HD1), normally neglected. It coincides with the “classic” THD when the distortion is mainly due to the 2nd order (on the left in the graph); it is higher than 10dB when it is due to the 3rd (right in the graph). Here more details on this aspect.
- The DSA (in gray, with an ordered reference on the right) which shows the percentage trend of the expanded transients; compressed ones are here equal to 1 - DSA, i.e. symmetrical. In line with what has already been seen, where the 2nd order prevails, there is a parity between expanded and compressed transients (“warm” effect); where 3rd order prevails there are only expanded transients (“dynamic” effect). Between -12dB and +3dB there is the transition from the first to the second situation, with a very pronounced slope.
The second graph shows the DSA and PSD curves for the simulated music-like signal, parameterized on three reference values of the 2nd harmonic: -110dB, -90dB and -70dB.
Fig. 10 - HD, True-THD, DSA (top) and PSD, DSA (below) per 3rd/2nd harmonic ratio (dB), with more 2nd harmonic references.
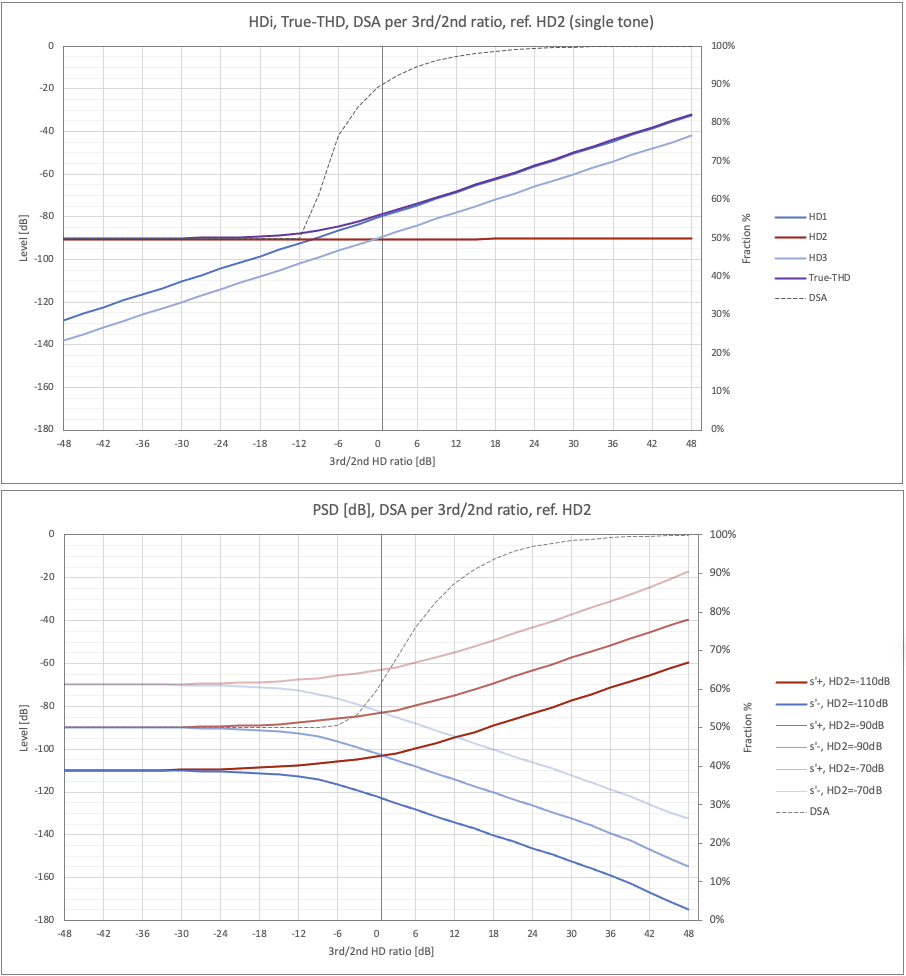
Here we observe that:
- The DSA curve (in gray, with ordinate reference on the right), similar in trend to that obtained for a single tone, less steep in the initial climb and shifted to the right. This highlights that the presence of more tones delays and makes the emergence of 3rd order dynamic effects more gradual. Furthermore, the curve is invariant with respect to the different reference levels: therefore, the mix of the two types of distortion on the transients depends only on the ratio of the levels of the two harmonics.
- The PSD curves are affected, as expected, by the variation of the 2nd order reference level which vertically translates the pairs of PSD+ (in red) and PSD- (in blue) curves by the same amount as the variation of the reference, 20dB. For a given reference level, where the 2nd harmonic prevails, the PSD curves remain constant and coincide with the value of the same reference; after that:
- The PSD+, associated with the expanded transients begins to increase around the 3rd/2nd harmonic ratio of -12dB, reaching a constant slope in addition to the 6dB ratio, similar to the trend of True-THD. Therefore, the dynamic effect due to 3rd harmonic distortion begins to act before the DSA increases, around -3dB.
- The PSD-, associated with the compressed transients, has a symmetrical trend to the PSD+, with an advance of the descent of about 10dB on the 3rd/2nd ratio. This indicates that, as the 3rd order increases, the amount of distortion on the same transients decreases, faster than the contributions to the expanded transients increase.
Let's now change the perspective, analyzing the distortions as a function of the level of the source signal. The graph in Figure 11 shows the True-THD, DSA and PSD curves at the input levels of 0dB, -10dB, -20dB and -30dB, setting the 2nd harmonic reference level at -70dB.
Fig. 11 - PSD, DSA per 3rd/2nd harmonic ratio (dB), for more input levels, ref. 2nd harmonic.
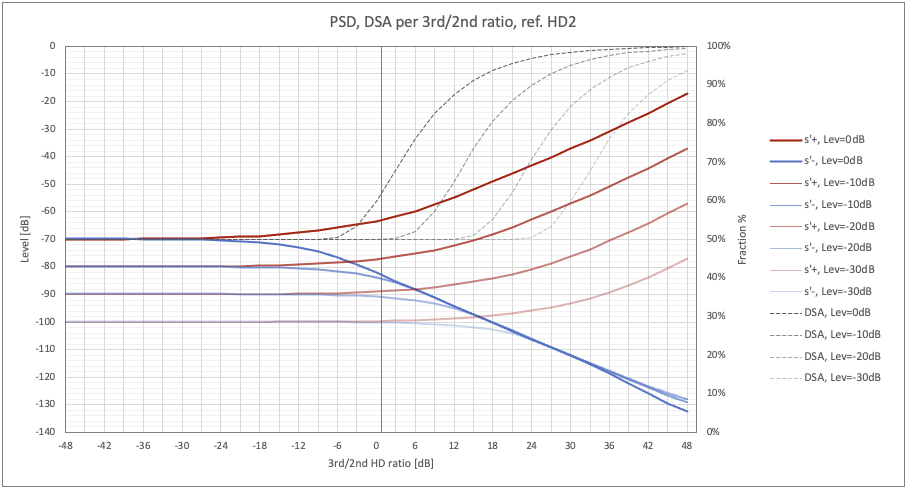
The DSA curves are different, and shift to the right by the same amount as the input level reduction. These effects are due to the fact that the 3rd order distortion decreases faster than the 2nd order one, respectively with the cube and square of the signal level. Therefore, with the same ratio between the two harmonics, the characteristic of the 3rd order distortion (dynamic effect) will “struggle” more to manifest itself as the input level decreases. The PSD curves are similar to those in fig. 10, shifted to the right and down by the same amount, 10dB.
It should be noted that these effects are obtained by acting on the volume of the reproduction if the amplifier has this control at the signal input or within the same piece of music when passing from parts to high to other lower levels and vice versa. This last aspect is more evident in the graph in fig. 12 which reports the DSA and PSD values as a function of the input level. The curves refer to different 3rd/2nd harmonic ratios (from 0dB to 30dB in 10dB steps), with the 2nd reference at -70dB.
It should be noted that these effects are obtained by acting on the volume of the reproduction if the amplifier has this control at the signal input or within the same piece of music when passing from parts to high to other lower levels and vice versa. This last aspect is more evident in the graph in fig. 12 which reports the DSA and PSD values as a function of the input level. The curves refer to different 3rd/2nd harmonic ratios (from 0dB to 30dB in 10dB steps), with the 2nd reference at -70dB.
Fig. 12 - PSD, DSA per 3rd/2nd harmonic ratio (dB), for more input levels, ref. 2nd harmonic.
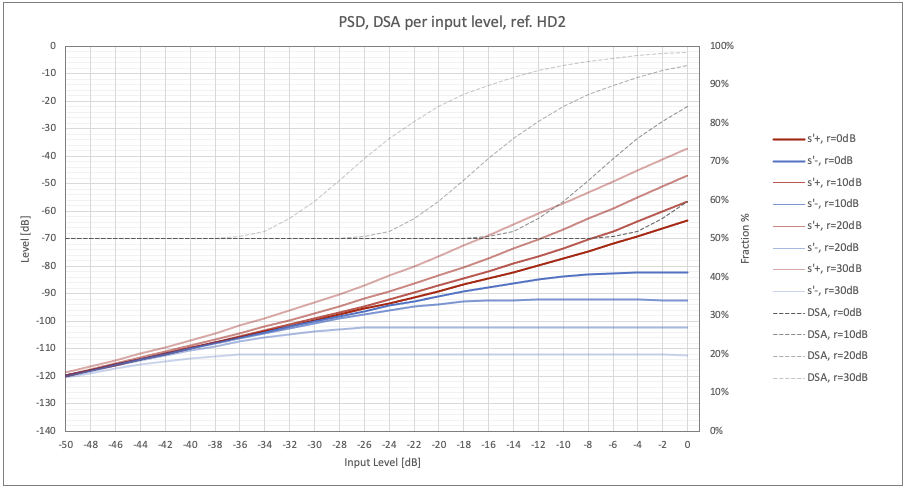
For low input levels the distortion is always dominated by the 2nd order characteristics, as evidenced by all the curves; for higher values of the input level the expansive effects of the 3rd order are felt, both on the DSA and on the PSD, so much stronger the higher the 3rd/2nd harmonic ratio. It should be added that the curves do not take into account the level of background noise which in practice hides the lowest levels of distortion. With the noise, the previous graph would be a straight line that, from high values at low input levels, drops progressively until the reported curves are intercepted.
Preliminary Conclusions
The above helps us to bridge the apparent gap between the subjective experiences of listening to music and the measures of non linear distortions. The study shows that the "dynamic" effect is probably caused by the expansive contributions of 3rd order distortion to the tones in the main signal, which strengthen its energy content and therefore the transients, to which we have a high sensitivity. These contributions are milder for the 2nd order, which distributes energy in the form of a "carpet", more pronounced in the medium-low frequencies. The presence of both orders of distortion produces intermediate effects, also dependent on the level of the input signal. With the DSA and PSD parameters we are able to numerically qualify these effects. And here we stop for now with speculations: to what extent a more or less large variation in physical quantities is perceived as more or less important must be experimented with listening tests.
Last edited: