Partitioned convolution discussion

[LionIT]

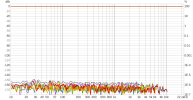
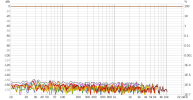
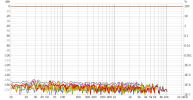
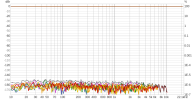
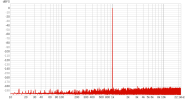
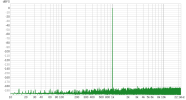
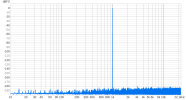
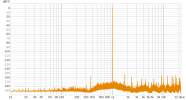
As is known, a popular method for room correction is to use convolution-applied FIR filters, and an ideal method to apply it is to use non uniform partitioned convolution (NUPC), because it allows acceptable latency with long FIR filters.
However, the NUPC is not a standard and fixed process, but can be configured in different ways.
A variable is the size of the initial block and successive blocks, which in addition to latency and computational load also seems to influence the signal, potentially in various ways.
Here, I would like to do discuss of this last aspect in order to understand what is the ideal block size to use for room correction.
Unfortunately I can't find a practical guide to doing this, so I did brainstorm with ChatGPT.
This is the result, on which I would like us to confirm the points or not (consider that there may be translation errors):

1. Linear convolution is partition invariant

Theoretically, partitioned convolution (even non-uniform) is an equivalent way of realizing the same linear convolution. So, if everything is done correctly, the processed signal does not change compared to direct convolution.

2. Possible differences in the signal arise from:

a. Overlap errors
Each block must be correctly aligned and added to its time window in the convolution.
If the temporal offset associated with each block is not precise (e.g. 256 samples offset for a 256 block), you may introduce phase shifts or comb filtering in the resulting signal.

b. Aliasing problems in FFT convolution
FFT uses circular convolution, so it is necessary to apply zero-padding and overlap-add (or overlap-save).
If you do not respect the correct padding, or if the FFTs are too short compared to the local IR of the block, you can introduce spectral aliasing or modify the frequency response.

c. Truncation and numerical precision
Small blocks truncate the IR to short segments. In NUPC, if the partitioning is too aggressive (e.g. small blocks for everything), you may miss important energy components of the IR in each block.
Furthermore, each FFT introduces floating point and round-off errors, which accumulate. If you use very small blocks, you increase the number of FFTs, thus amplifying the numerical error.

3. Frequency domain reflection

The accuracy of the frequency representation is better with longer FFTs. Small blocks have short FFTs, thus a low frequency resolution.
This means that any manipulation or filtering in the frequency domain (e.g. with HRTFs or dynamic filters) will have less precision if you apply too short FFTs.

4. Leakage and discontinuity phenomena

If you apply time windows (e.g. Hann) on the blocks before the FFT, smaller blocks introduce more leakage.
If you do not apply windows, but the blocks do not match perfectly at the edges (especially in non-uniform cases), discontinuities and therefore transient artifacts can be generated.

5. Effects of Block Size on Transients

• Smaller blocks (e.g. 64-128 samples):
Allow for faster response to changes in the signal, faithfully reproducing transients.
Require more processing power, as they increase the number of FFT/IFFT operations.

• Larger blocks (e.g. 1024-4096 samples):
May cause delays in the transient response, smoothing or attenuating fast details.
They are more computationally efficient, reducing the load on the CPU.


Do you think these things can be confirmed?
If so, can we determine an ideal size for first and subsequent blocks?

 

[Keith_W]

Interesting thread. I must admit that I have not thought about it much. I use Acourate Convolver, which allows you to specify chunk size. I have also been experimenting with CamillaDSP, which allows you to do the same.

But first, I would like to check my understanding. My understanding is that chunks are very roughly analogous to buffers. If we have a 48kHz sample rate, it is inefficient for the CPU to grab samples from memory 48000 times per second. The performance of our CPU will slow to a crawl. So we have buffers which fill up with samples, and the CPU grabs everything in the buffer and processes it in one fell swoop. The problem is if the buffer is too small - not only does this mean the CPU has to fetch more often, there is a risk that the buffer may be empty when the CPU tries to grab data.

I think that chunks are the same, but with the added complications that you mention. Small chunks require more CPU power, otherwise audible glitches will occur. Certainly in my experiments, using very small chunks reduces latency, but results in audible dropout and glitchy artefacts if it is too small. I was not aware of the other complications you mentioned, but it does seem to make sense.

Perhaps @HenrikEnquist or @gberchin would like to chime in?

 

[LionIT]

I don't know who the DSP Guru are here so I haven't invoked them.
If they wanted to join the discussion it would be very constructive.


I honestly have doubts about the relationship between block size and transients (point 5 of first post).
I understand that a certain block length is needed to make FFT and that the frequency resolution depends on it. But I find it harder to understand how the length affects transients.
It is really correct the point 5?
If so, what would the mathematical relationship be?
If there is effect on transients, it should be necessary to identify an optimal value then.

PS. I use the free MCFX convolver that should apply NUPC, and that allows you to set the size of the initial block and the maximum size of the subsequent blocks.

 

[HenrikEnquist]

1. Linear convolution is partition invariant

Theoretically, partitioned convolution (even non-uniform) is an equivalent way of realizing the same linear convolution. So, if everything is done correctly, the processed signal does not change compared to direct convolution.

This is the most important part. Unless there are bugs, the result is the same no matter what, except for numerical noise which will be different for different implementations anyway.

2. Possible differences in the signal arise from:

Here, a & b would be easily detected bugs. The first half of c is mostly nonsense, but the second half about rounding is true. However already with 32-bit floats any correct implementation will get a noise level in the vicinity of -150 dB (and -300 dB for 64-bit) so not an issue.

Points 3-5 are nonsense, because point 1

 

[LionIT]

This is the most important part. Unless there are bugs, the result is the same no matter what, except for numerical noise which will be different for different implementations anyway.



Here, a & b would be easily detected bugs. The first half of c is mostly nonsense, but the second half about rounding is true. However already with 32-bit floats any correct implementation will get a noise level in the vicinity of -150 dB (and -300 dB for 64-bit) so not an issue.

Points 3-5 are nonsense, because point 1

In fact, brainstorming with Gemini I got this conclusion:

In principle, the block size chosen for partitioned convolution (uniform or non-uniform) does not alter the way the filter modifies the signal, provided the implementation is correct.
Here's why:
* Mathematically Identical Result: Partitioned convolution is an optimized implementation technique for computing the result of linearly convolving an input signal and an impulse response (the filter). The goal is to obtain exactly the same result as if you were to perform a single, long direct or FFT-based convolution (as with standard Overlap-Add or Overlap-Save) between the entire signal and the entire impulse response.
* Correct Reconstruction: The method decomposes the impulse response into blocks (partitions). Each block is convolved separately with appropriate segments of the input signal. The partial results are then summed and correctly superimposed (handling delays and overlaps) to reconstruct the final output. If this recomposition is done correctly, the result is mathematically identical to the unpartitioned convolution.
* Latency vs. Filter Characteristic: The choice of block size (especially in the non-uniform case) mainly affects:
* Latency: Smaller blocks at the beginning reduce the latency for the early and perceptually most important parts of the impulse response.
* Computational Load (CPU): Larger blocks for the later parts reduce the number of operations (FFT, multiplications, additions) needed per unit of time, optimizing CPU usage.
* It does not affect the intrinsic characteristic of the filter (its frequency response, how it attenuates or boosts certain frequencies, or how it "smears" the signal in time). That is defined solely by the impulse response itself, not by how the convolution is computed.
Possible (but generally not problematic) Subtleties:
* Implementation Errors: If there were errors in the code that handles overlaps and sums of partial results, then yes, artifacts could occur and the result would be different. But this would be a bug, not an intrinsic consequence of the block size choice.
* Numerical Precision: The use of floating point arithmetic in FFTs inevitably introduces very small numerical inaccuracies. The order and grouping of operations, which may vary slightly with different block sizes, could lead to tiny differences in the least significant bits of the final result. However, these differences are almost always completely inaudible and well below the noise floor of any practical audio system. They do not represent an audible or significant change in filtering.
Bottom line: You can think of partitioned convolution as a clever way of "doing the math" to achieve the same result as standard convolution, but with better latency and resource management. The choice of block size is a matter of performance (latency and CPU), not of altering the sound produced by the filter. The filter will always do "the same thing" to the signal, regardless of how you choose to partition the computation.

So if the convolver is programmed correctly, the only dependencies of the block size are latency and CPU load, correct?

 

[Holmz]

I don't know who the DSP Guru are here so I haven't invoked them.

Or maybe conjured is the operative phrase?

If they wanted to join the discussion it would be very constructive.


I honestly have doubts about the relationship between block size and transients (point 5 of first post).

Me too.

I understand that a certain block length is needed to make FFT and that the frequency resolution depends on it. But I find it harder to understand how the length affects transients.
It is really correct the point 5?
If so, what would the mathematical relationship be?
If there is effect on transients, it should be necessary to identify an optimal value then.

PS. I use the free MCFX convolver that should apply NUPC, and that allows you to set the size of the initial block and the maximum size of the subsequent blocks.

Optimal delay is 0.
Optimal transient response is 1 (or maybe infinity depending on how one defines it.)

The optimal block size would be the time that the block covers being >= or the group delay.
One could probably determine the optimal sample rate with how quickly things are changing in the frequency domain, but once one gets past room modes… and especially up to the tweeter, then the driver is generally linear.

Cone breakup, cabinet and basket resonances are not really things that a DSP should be used to address, and those largely are non-linear.

 

[gberchin]

Points 1-2 just describe basic arithmetic and proper implementation of it. If you can't figure out how to align buffers in your computer program, you probably shouldn't be programming.

Point 3 is correct, but only becomes an issue when your filters have steep transition bands, narrow and deep notches, etc. As such, I wouldn't call it "Frequency domain reflection", I'd call it "Frequency domain resolution".

Point 4 is ambiguous. If you are performing spectral analysis, then the window affects your ability to resolve individual spectral peaks, or noise amplitude, for example. If you are performing filtering, then you are limited to windows that provide perfect reconstruction (windows overlap in time such that they sum to 1.0), otherwise you are corrupting your data.

Point 5 is utter nonsense. If properly implemented, then the block size has absolutely no effect upon the results of the signal processing, other than the input-to-output time delay. What block size does affect is computational efficiency. If performing FFTs, for example, an FFT that is twice as long involves less than twice as much processing. Also, other operations such as filtering can benefit from block processing because subroutine calls involve overhead, and it's better to amortize that overhead over a large number of samples than over a small number of samples. Finally, keep in mind that processing can often be run in parallel, particularly in multicore processors, meaning that one block of samples can be fetched/stored while another block of samples is being processed.

EDIT: Correction; an FFT that is twice as long requires slightly more than twice as much processing, but not as much of an increase as with direct convolution. FFT increases as O(n log n) while direct convolution increases as O(n²).

 

[voodooless]

There is no relation between block size and transients. It's a fully transparent algorithm, no matter the block size. Block size is just a parameter for tuning latency and CPU/memory efficiency.

Similarly, smaller block sizes also do not impact frequency resolution because you end up with a superposition of multiple blocks. This is true up to a point. In a real-world implementation, 64 or 128 should be a good lower bound.

You will need to make sure you have sufficient math precision for all of this. 64-bit float is fast enough and works perfectly well.

 

[gberchin]

64-bit float is fast enough and works perfectly well.

In fact 64-bit float is generally overkill. I once implemented the same FFT-based (FFT size > 16K) audio processing in both 32-bit float and 64-bit float, and compared the results. They were bit-for-bit identical. That is not always the case, but for audio it is pretty rare that 64 bits are really necessary.

 

[bmc0]

The answers given by @HenrikEnquist, @gberchin, and @voodooless are correct. I'll add a little bit of data from two convolution engines I wrote myself. One does simple non-partitioned FFT convolution while the other does multithreaded non-uniform partitioned convolution where the first partition is direct[1] and the rest are FFT. Here are the results of a null test when applying a reverb impulse (~1s long) to a music track:

Channel                       L            R
Peak level (dBFS)     -303.5288    -304.2845
RMS level (dBFS)      -322.2496    -322.3476

As expected, the outputs are identical, save for rounding error.

Regarding computational efficiency and realtime latency, there are a number of papers on the subject. Here's one that I found useful.

[1]: Using direct convolution for the first partition enables zero added input-output latency without input block size constraints. Most of the time, this isn't actually useful since the block size to/from the audio device is often known, but I had reasons to do it this way in this particular case.

 

[Daverz]

The brutefir docs have some discussion of partitioned convolution.

BruteFIR

Usually one would just use the suggested default for your sampling rate (e.g. as in the CamillaDSP docs) and only adjust it if you experience dropouts.

 

[LionIT]

The answers given by @HenrikEnquist, @gberchin, and @voodooless are correct. I'll add a little bit of data from two convolution engines I wrote myself. One does simple non-partitioned FFT convolution while the other does multithreaded non-uniform partitioned convolution where the first partition is direct[1] and the rest are FFT. Here are the results of a null test when applying a reverb impulse (~1s long) to a music track:

Channel                       L            R
Peak level (dBFS)     -303.5288    -304.2845
RMS level (dBFS)      -322.2496    -322.3476

As expected, the outputs are identical, save for rounding error.

Regarding computational efficiency and realtime latency, there are a number of papers on the subject. Here's one that I found useful.

[1]: Using direct convolution for the first partition enables zero added input-output latency without input block size constraints. Most of the time, this isn't actually useful since the block size to/from the audio device is often known, but I had reasons to do it this way in this particular case.

If I try to measure in digital loopback the 24-bit audio signal passed into partitioned convolver with 32-bit Dirac Pulse, I get a noticeable elevation of THD+N. It goes from about -140dBFS of the original signal to -100dBFS about when processed by the convolver.
According to the approximate calculations it takes about 10k mathematical operations for the quantization error to raise the level thereby, which from an estimate could correspond to those performed by a convolver with a long IR.
However with a Dirac Pulse Operations should not lead to numerical alteration (it's 1,0,0,0,0,...).
Is it possible that the countless mathematical operations also introduce a lot of noise?
As previously said, I'm using MCFX convolver.

 

[bmc0]

If I try to measure in digital loopback the 24-bit audio signal passed into partitioned convolver with 32-bit Dirac Pulse, I get a noticeable elevation of THD+N. It goes from about -140dBFS of the original signal to -100dBFS about when processed by the convolver.

There's something wrong somewhere, it would seem. This is what I get when I convolve a REW measurement sweep (44.1kHz, 512k samples, 32-bit integer) with a one second long Dirac pulse—
Original sweep:

Simple 64-bit FFT convolver (no partitioning):

Non-uniform partitioned 64-bit direct/FFT convolver:

Non-uniform partitioned 32-bit FFT convolver (zita-convolver library):


First three are identical with the noise floor set by the sweep length (I believe). 32-bit float NUPC increases noise very slightly.

 

[LionIT]

There's something wrong somewhere, it would seem. This is what I get when I convolve a REW measurement sweep (44.1kHz, 512k samples, 32-bit integer) with a one second long Dirac pulse—
Original sweep:
View attachment 444660
Simple 64-bit FFT convolver (no partitioning):
View attachment 444661
Non-uniform partitioned 64-bit direct/FFT convolver:
View attachment 444662
Non-uniform partitioned 32-bit FFT convolver (zita-convolver library):
View attachment 444663

First three are identical with the noise floor set by the sweep length (I believe). 32-bit float NUPC increases noise very slightly.

Sorry could you try to make the same measures with MCFX?
I am using the Mac version, but I suppose it does not change the result on other systems.
I see that on linux It also use zita-convolver.
Without it I also get TD+N at -140dbfs about as expected from the bit depth.
I'm sure my IR is correctly a Dirac Pulse.

 

[bmc0]

Sorry could you try to make the same measures with MCFX?

I may try later; I'd have to build it from source though.
Here's the spectrum of a 1kHz tone using the same convolvers as above (easier to see the difference this way):

Total integrated noise for 32-bit NUPC (yellow) is -137dBFS.

 

[LionIT]

I may try later; I'd have to build it from source though, it would seem.

Pre-built releases are available in the repository (Mac/Win).
Which convolver are you using?

 

[bmc0]

Pre-built releases are available in the repository.

Not for Linux though .

 

[bmc0]

Which convolver are you using?

Sorry, I didn't see this question. I implemented the 64-bit convolution engines myself. The 32-bit example is the zita-convolver library. The main point, however, is that the increased noise/distortion you measured is not inherent to partitioned convolution. I did not do anything special to improve the numerical performance.

What does the spectrum look like? Is the degraded TD+N due to noise (16-bit dither, perhaps?) or nonlinear distortion?