A few days ago, someone in a QQ Group said, "Recently, a new R2R decoder called Pegasus has been released, which is very cheap." I think to myself: Don't use Soekris's DIY products again, right? Then I went to Taobao and found this product. The first impression was: Hey, this design is quite interesting! And after Google, I found that the internal circuit design is different from the R2R I tested before. Hmmm... The new power of ChiFi? Then we have to find a way to measure it! After an inquiry in social relations, a friend finally had a machine willing to lend me a measurement!Today, it arrived:

Overall completion is very high! Chassis workmanship value for money! There are enough input ports. The main disadvantage... is that there is no remote control... Emmmm... it will be a bit inconvenient...But I found an interesting place... Is the AC of this device a global voltage? No need to switch? That's not right... The internal map I saw earlier on Google clearly used an O-type transformer? No, I have to look at ...... open after obtaining permission disassemble ...... I took it apart:


A brief look at the circuit, the Mingwei switching power supply in the upper left corner will be turned on at the first time of 220V input, and then through the detection circuit to determine whether it is currently 220V or 110V input, the main control circuit will then select the corresponding relay to determine ON mode transformer winding ...... Emmmm very good design!It reduces the possibility of malfunction caused by someone dialing the wrong rear voltage switch, and also reduces SKUs, praise!However, there is still a small detail that can be improved as a whole: I hope that future machines of this brand will work hard on the magnetic shielding of the transformer. The current layout should still be able to see the effect of magnetic leakage in the measurement (though in fact, everyone It's almost the same... I'm nitpicking)
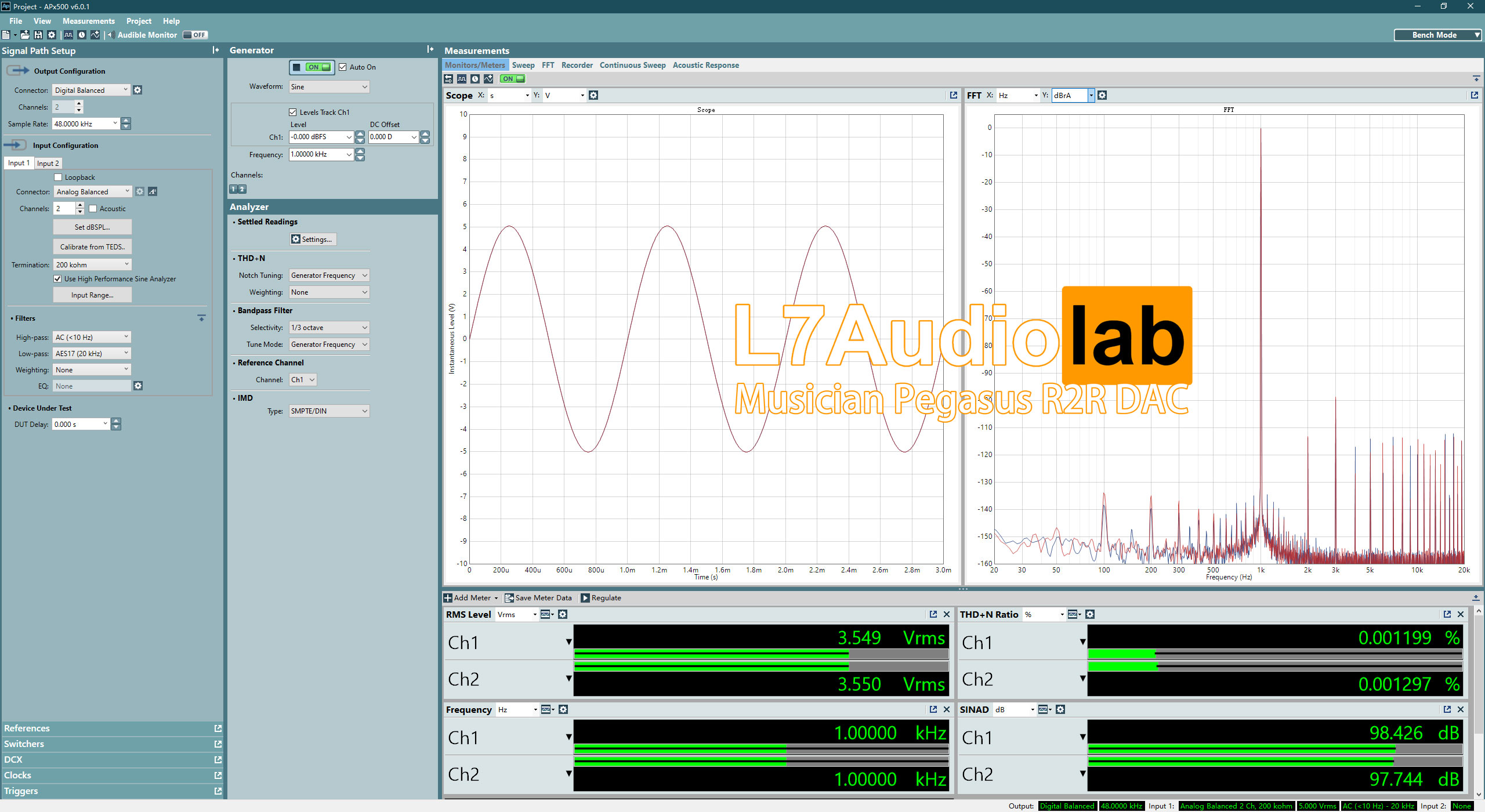
The XLR level of 3.55V... It will be a bit disadvantaged when comparing equipment (the volume will be lower), but the overall performance can be said to be pretty good in the discrete R2R! It obviously surpasses the devices like D1000 and AudioGDR8 I have measured before. Although there is still a gap with HoloAudio's R2R, this is an entry-level product. Well done Musician! Well done!
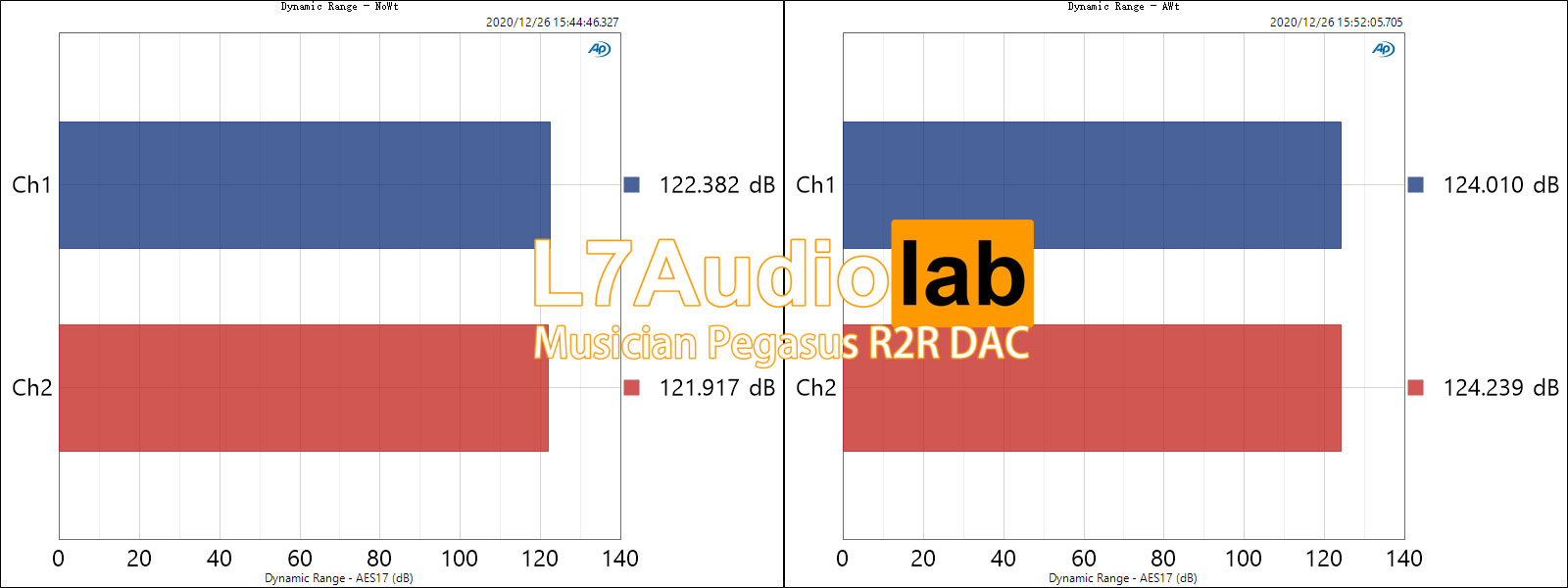
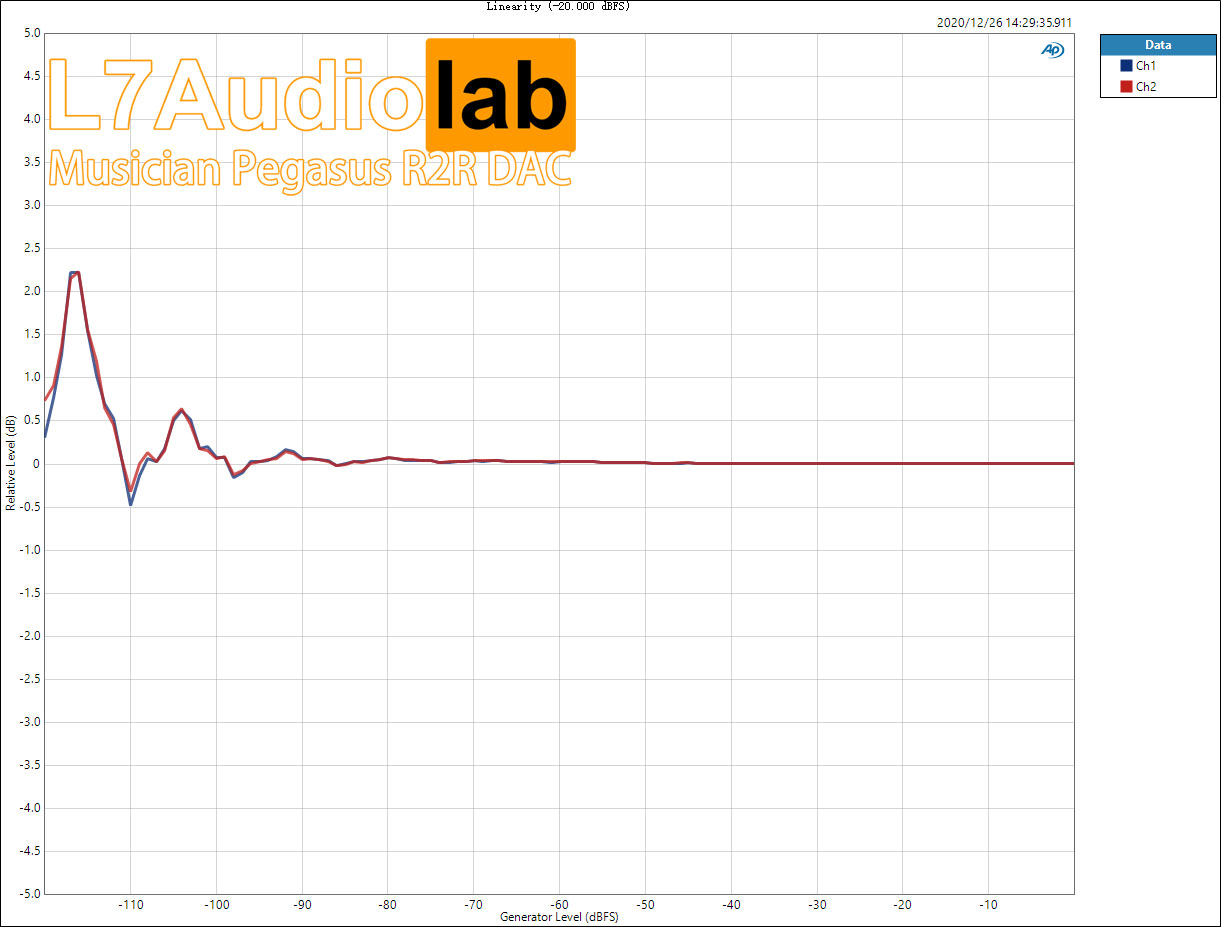
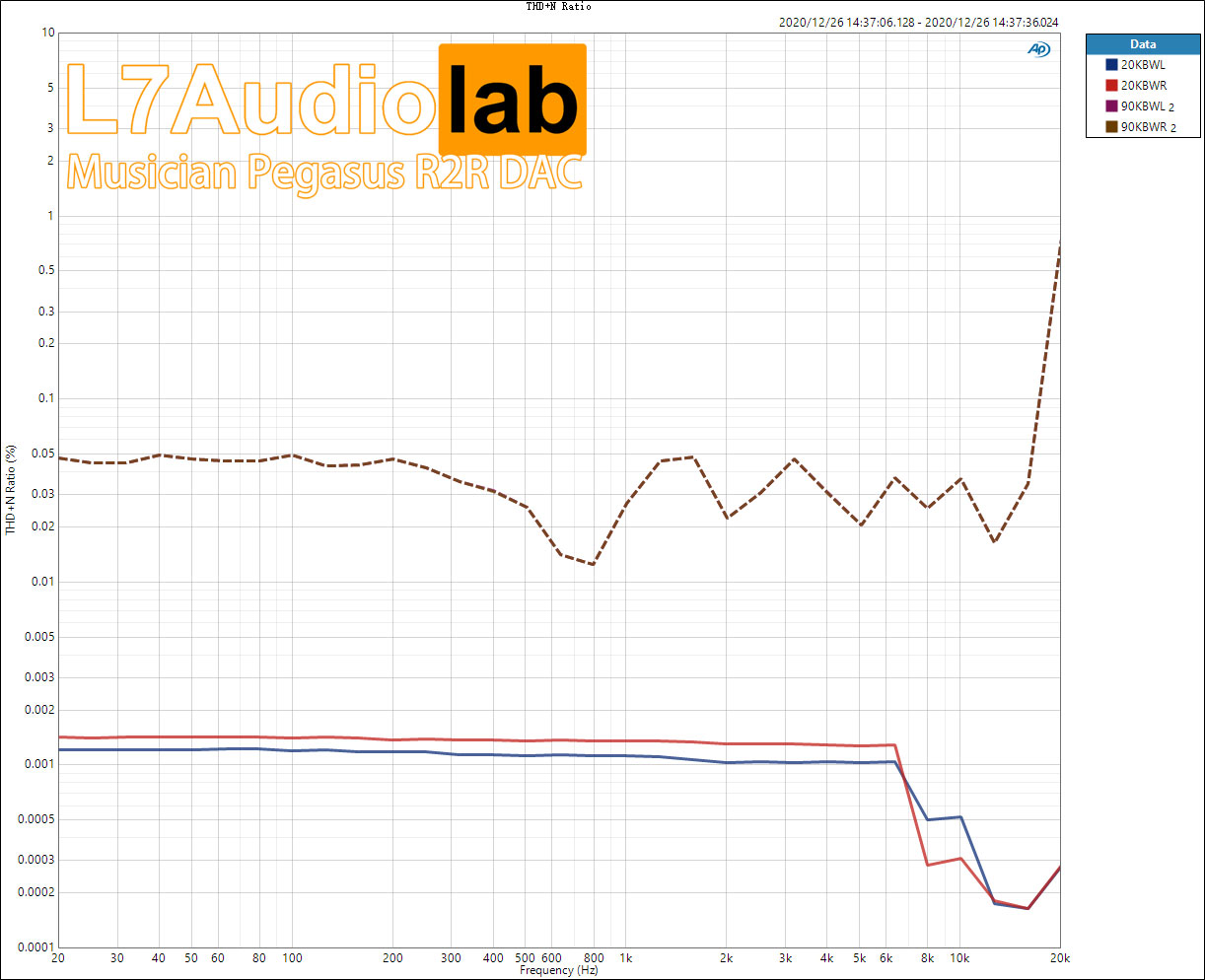
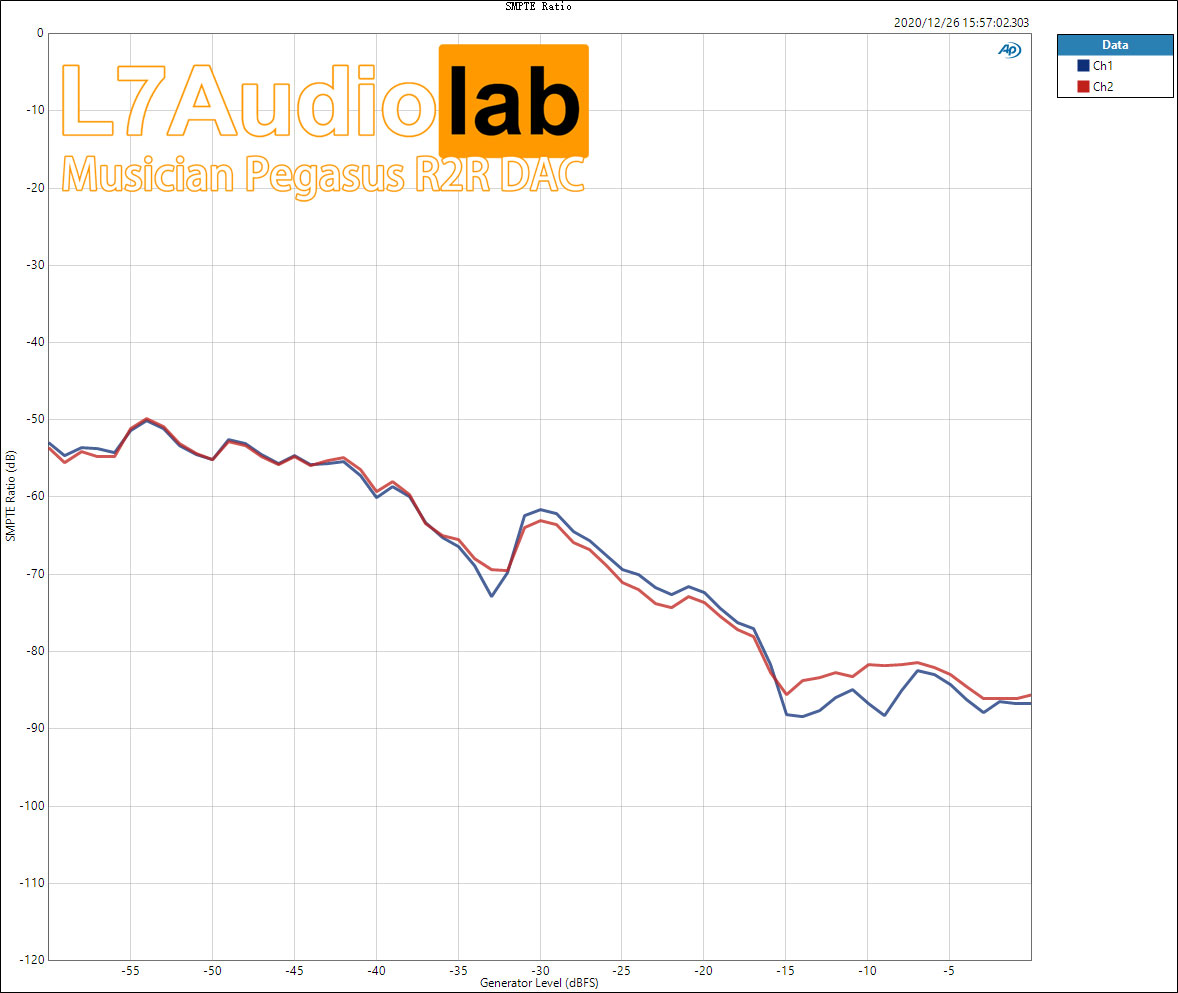
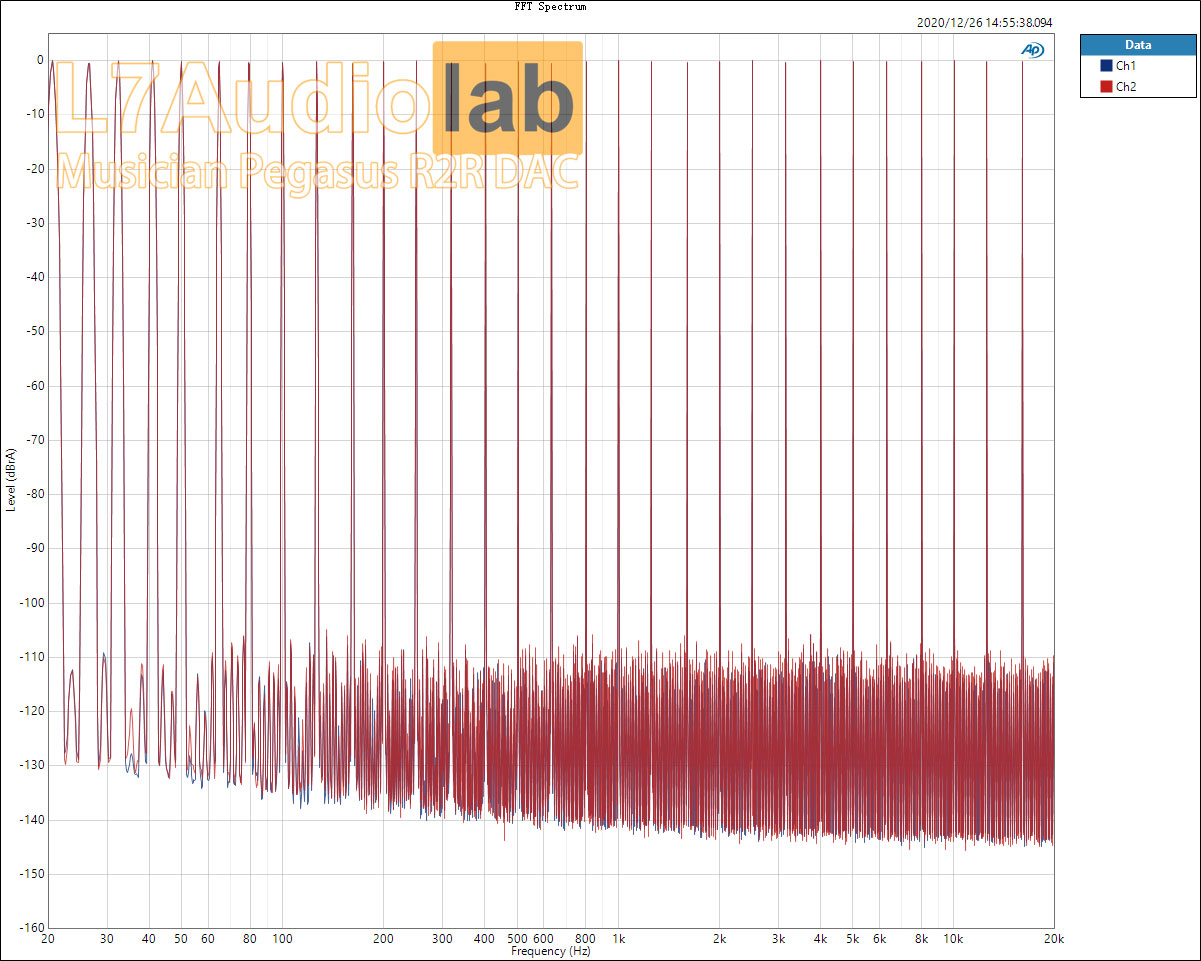
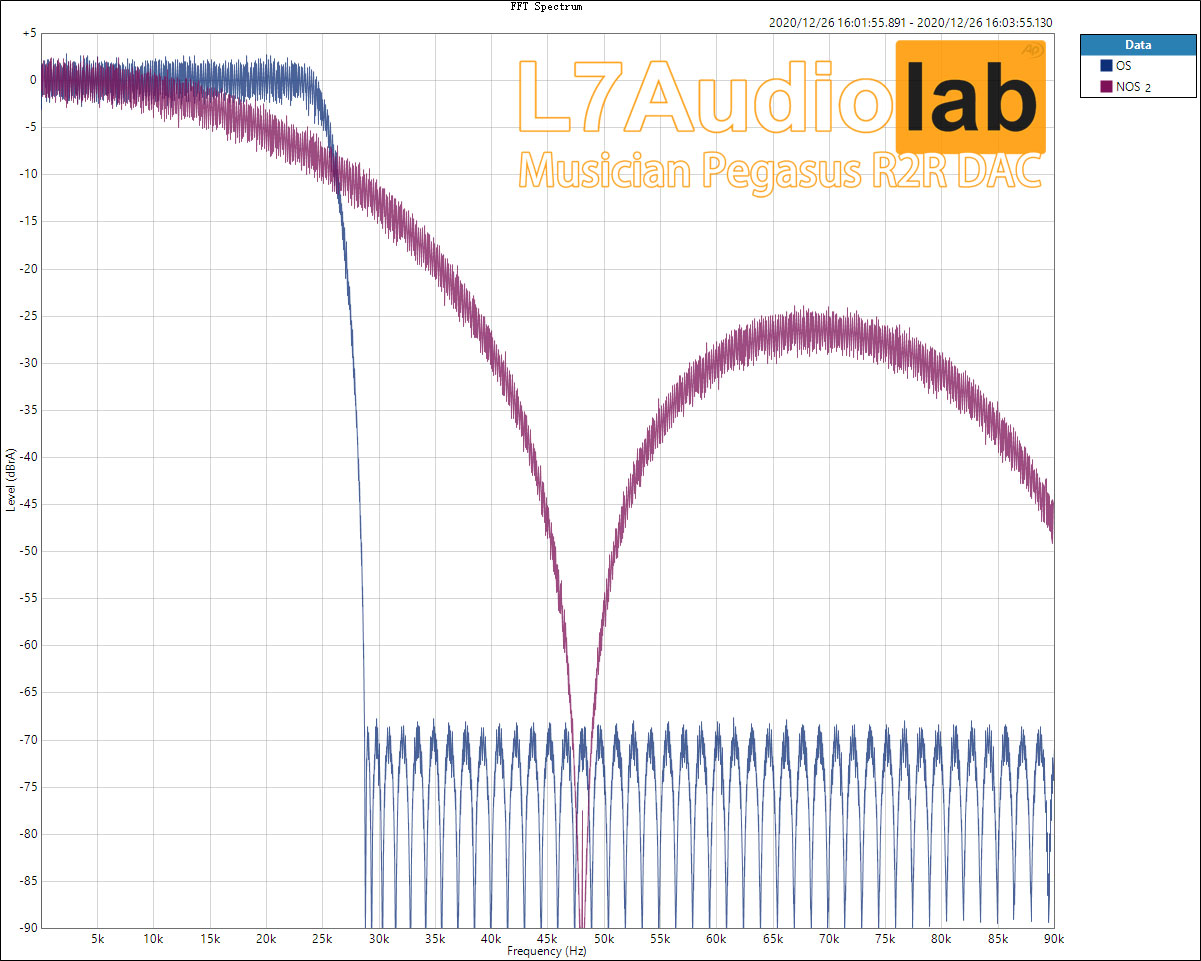
Summary: In this price range, there were really no outstanding products for discrete R2R before. What's commendable is that the Pegasus has also made some good designs, and the chassis makes people feel ecstatic. I even think that if the decoding of 4499 is put on this shell, the price will be sold beyond the price of this product... Personally feel that it is really full of sincerity... As a new force in ChiFi, I think Musician will continue to follow this trend... ...The future can be expected.
Overall completion is very high! Chassis workmanship value for money! There are enough input ports. The main disadvantage... is that there is no remote control... Emmmm... it will be a bit inconvenient...But I found an interesting place... Is the AC of this device a global voltage? No need to switch? That's not right... The internal map I saw earlier on Google clearly used an O-type transformer? No, I have to look at ...... open after obtaining permission disassemble ...... I took it apart:
A brief look at the circuit, the Mingwei switching power supply in the upper left corner will be turned on at the first time of 220V input, and then through the detection circuit to determine whether it is currently 220V or 110V input, the main control circuit will then select the corresponding relay to determine ON mode transformer winding ...... Emmmm very good design!It reduces the possibility of malfunction caused by someone dialing the wrong rear voltage switch, and also reduces SKUs, praise!However, there is still a small detail that can be improved as a whole: I hope that future machines of this brand will work hard on the magnetic shielding of the transformer. The current layout should still be able to see the effect of magnetic leakage in the measurement (though in fact, everyone It's almost the same... I'm nitpicking)
The XLR level of 3.55V... It will be a bit disadvantaged when comparing equipment (the volume will be lower), but the overall performance can be said to be pretty good in the discrete R2R! It obviously surpasses the devices like D1000 and AudioGDR8 I have measured before. Although there is still a gap with HoloAudio's R2R, this is an entry-level product. Well done Musician! Well done!
Summary: In this price range, there were really no outstanding products for discrete R2R before. What's commendable is that the Pegasus has also made some good designs, and the chassis makes people feel ecstatic. I even think that if the decoding of 4499 is put on this shell, the price will be sold beyond the price of this product... Personally feel that it is really full of sincerity... As a new force in ChiFi, I think Musician will continue to follow this trend... ...The future can be expected.
