This is a review and detailed measurements of the Klipsch R-41M bookshelf speaker. I bought a pair from Amazon for US $149. The retail cost is US $229 but I suspect no one pays that.
I always say speaker business is 80% marketing and Klipsch nails that with look and branding of this series of speakers:

You go into evaluation wanting it to sound good. After all, it even says it is "reference" quality speaker. Definitely a genius at work here.
The back panel sports nice (for the price) speaker terminals:

Hopefully the side panels are thicker than they look and the back panel is inset into them.
Measurements that you are about to see were performed using the Klippel Near-field Scanner (NFS). This is a robotic measurement system that analyzes the speaker all around and is able (using advanced mathematics and dual scan) to subtract room reflections. It also measures the speaker at close distance ("near-field") which sharply reduces the impact of room noise. Both of these factors enable testing in ordinary rooms yet results that can be more accurate than anechoic chamber. In a nutshell, the measurements show the actual sound coming out of the speaker independent of the room. All measurements are reference to tweeter axis with the grill removed.
Over 1000 points around the speaker were measured (from 20 to 20 kHz) which resulted in well under 1% error in identification of the sound field emanating from the speaker up to about 18 kHz. Above that the error increases slightly. Final database of measurements and data is 1.4 Gigabytes in size.
Spinorama Audio Measurements
Acoustic measurements can be grouped in a way that can be perceptually analyzed to determine how good a speaker can be used. This so called spinorama shows us just about everything we need to know about the speaker with respect to tonality and some flaws:
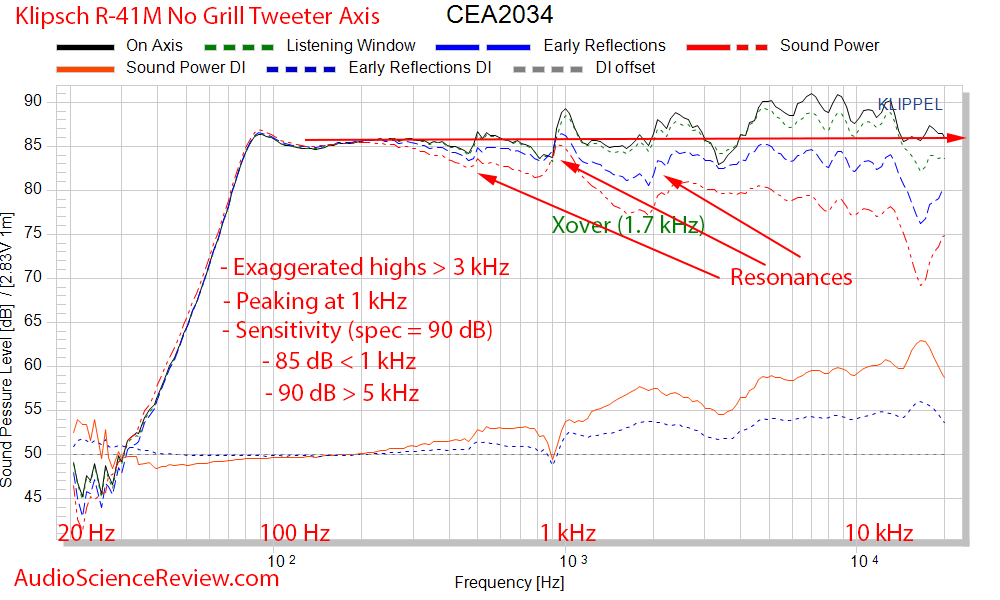
Boy, oh boy! Where to start. Let's start with that peak at 1 kHz. What on earth is that? It reminds me of Pinocchio's nose! I know Klipsch is known for bright highs but must we also throw in all those resonances as indicated by peaks that show up in all four upper graphs?
Since we fed the speaker 2.83 volts for measurements, the frequency response also becomes the sensitivity graph. We see that during much of the low spectrum were most of the music energy is, sensitivity is at 85 dB. It only gets to 90 dB during those terrible highs. So don't make the mistake of thinking this is an efficient speaker, it is not.
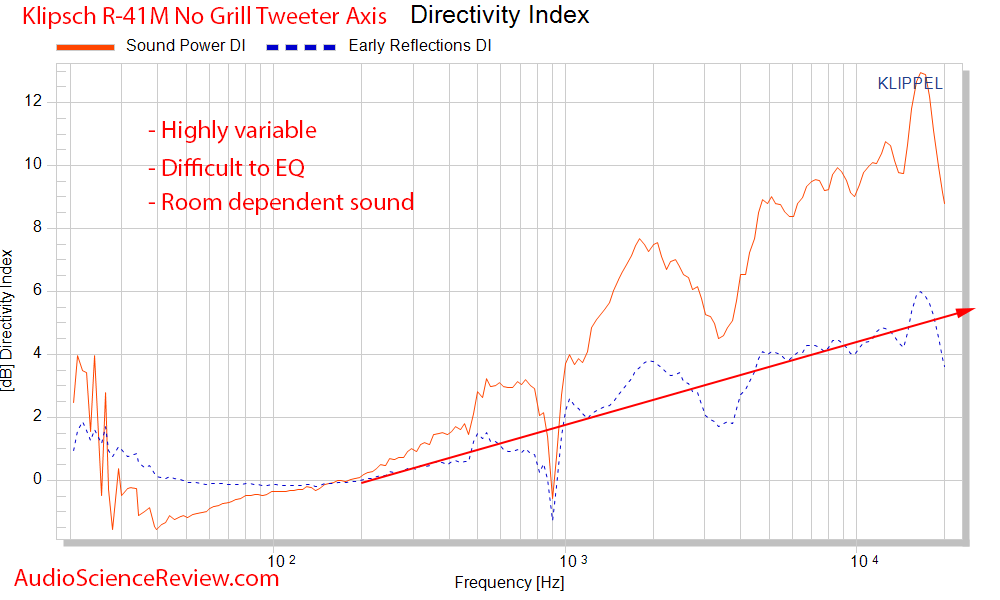
Direcitivty index graph needs to be smooth to allow us to fix the frequency response anomalies we see above but it is not:
Predicted in-room response fortunately is not as bad as on-axis:
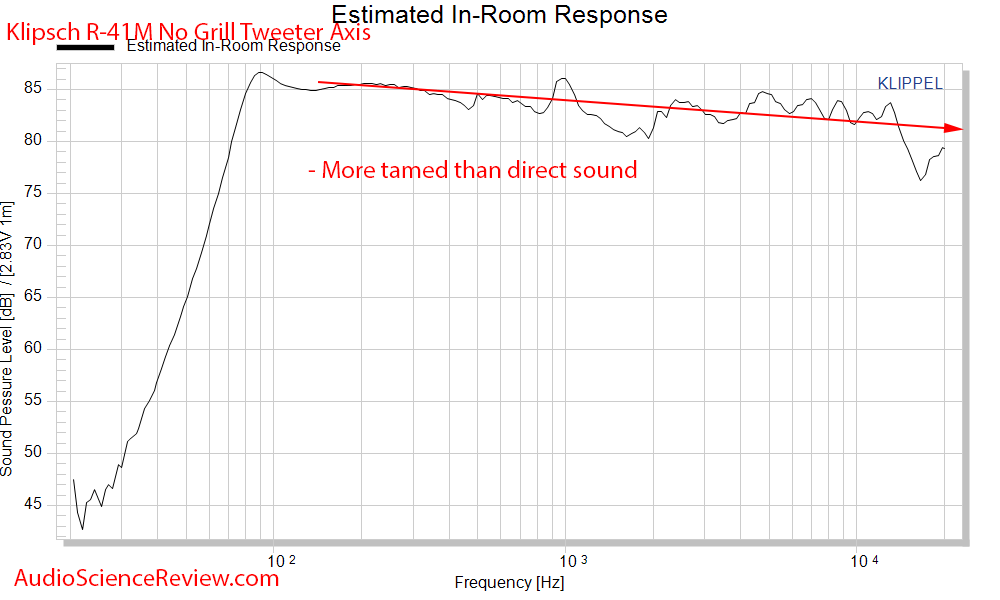
The hotness of the tweeter wears off when not listened to on-axis, improving the response some. Still nothing to write home about unless you want this type of EQ applied to every piece of music you play. The people who incorrectly think everyone's taste in speakers is different can perhaps explain why some people may want every note around 1 kHz in their music to be exaggerated.
So we are done with how this speaker is going to "sound." It is going to sound very bright and uneven on-axis (speaker pointed at your ears). Toed out it will sound better but the measurements say avoid this speaker.
Basic Speaker Measurements
Impedance measurements show that the Klipsch spec of 8 ohms is a fantasy:
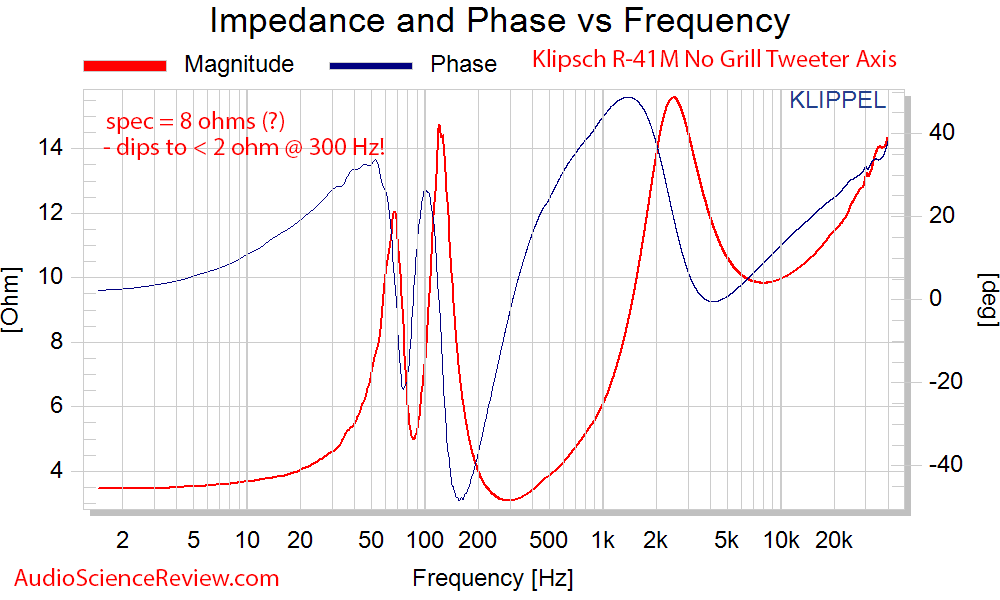
Response dips dangerously close to a short at 300 Hz or so. You better have a lot of amplification power there especially since sensitivity is low there as well.
There are a lot of kinks and such that indicate issues which I am not bothering to outline. They are also (potentially) visible in the waterfall measurements:
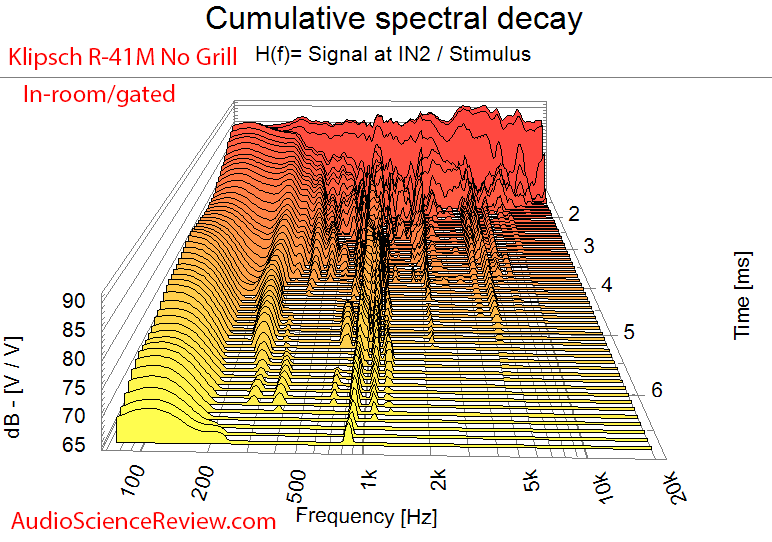
Then again we saw them so clearly in frequency response measurements including that 1 kHz peak.
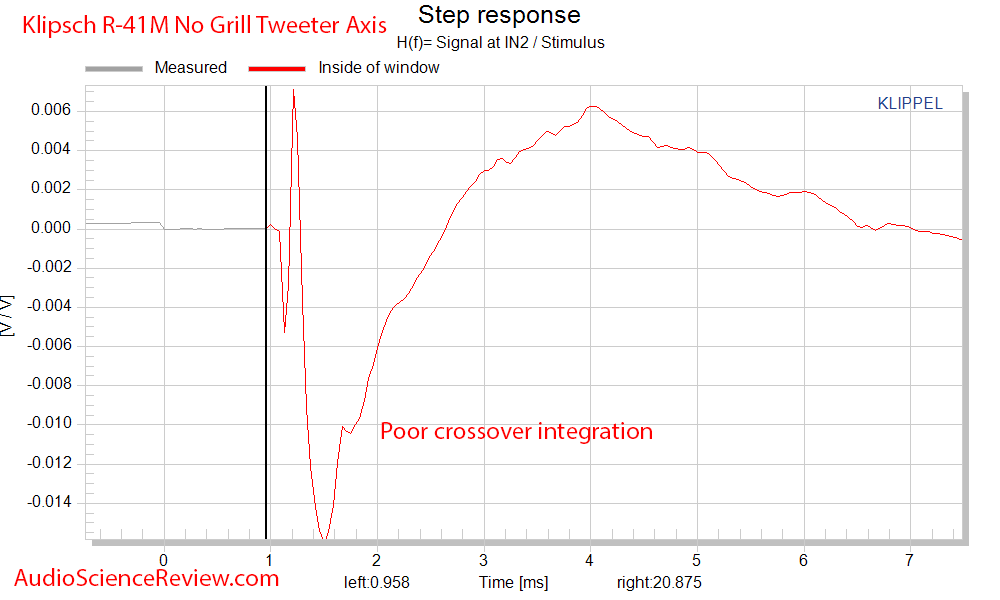
Step function shows a kink as the tweet to woofer transition showing poor crossover design:
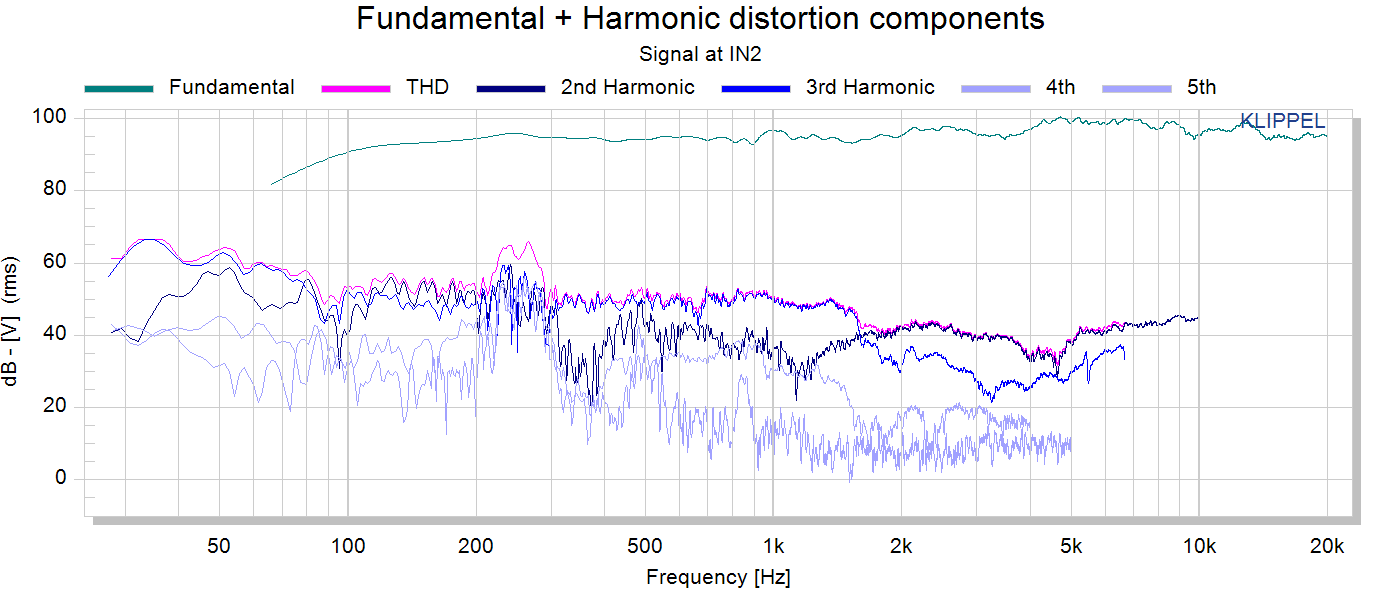
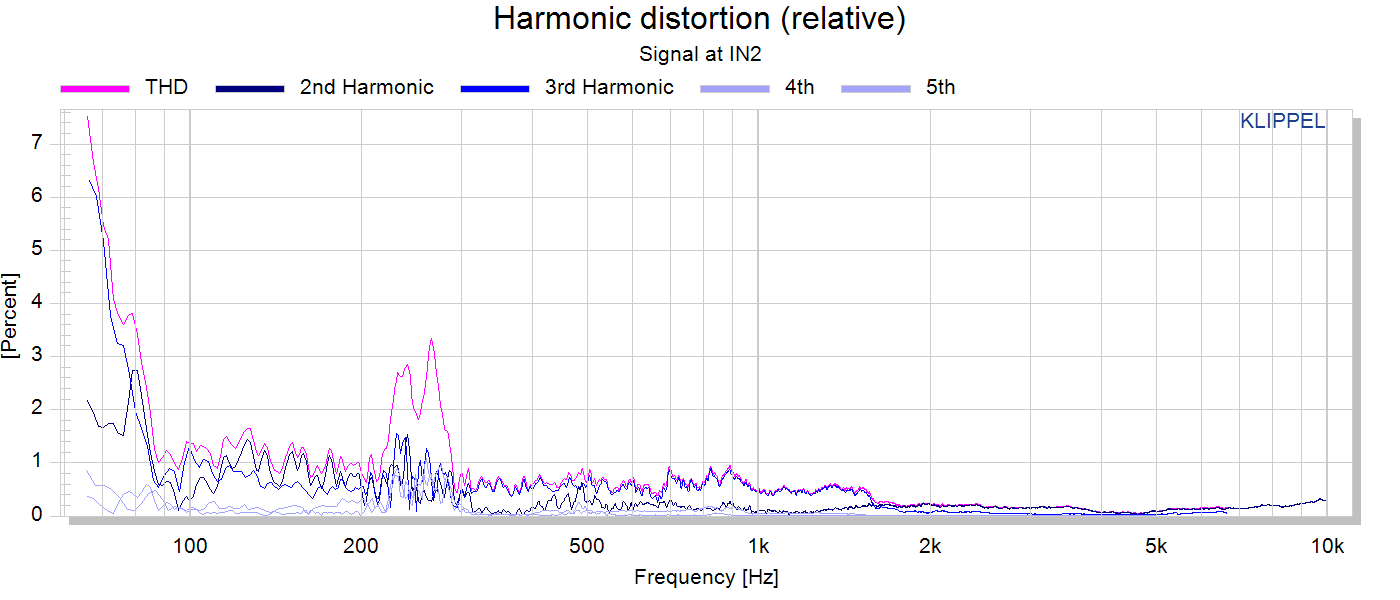
Continuing our low quality measurements we get to distortion:
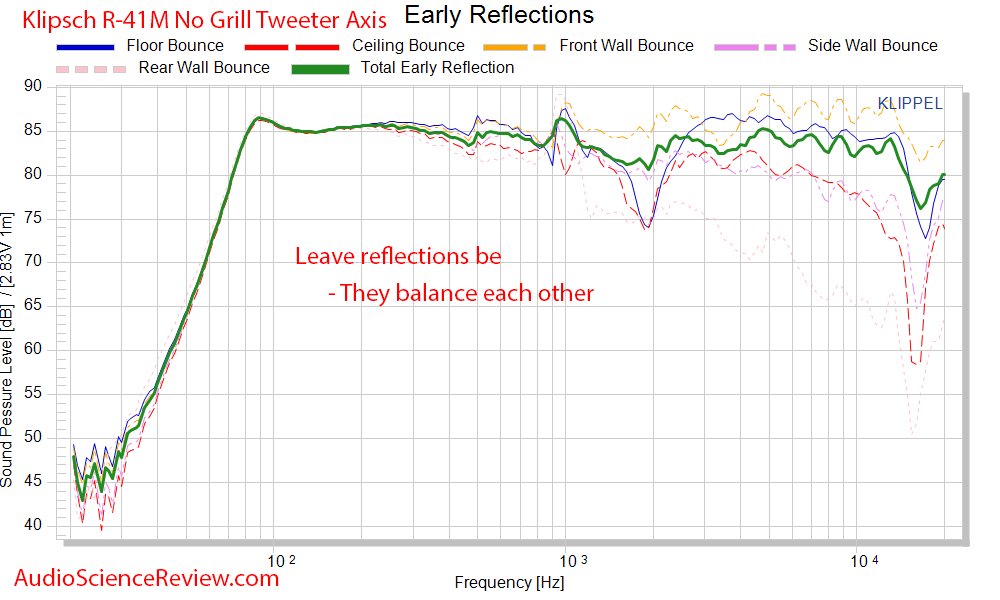
Advanced Speaker Measurements
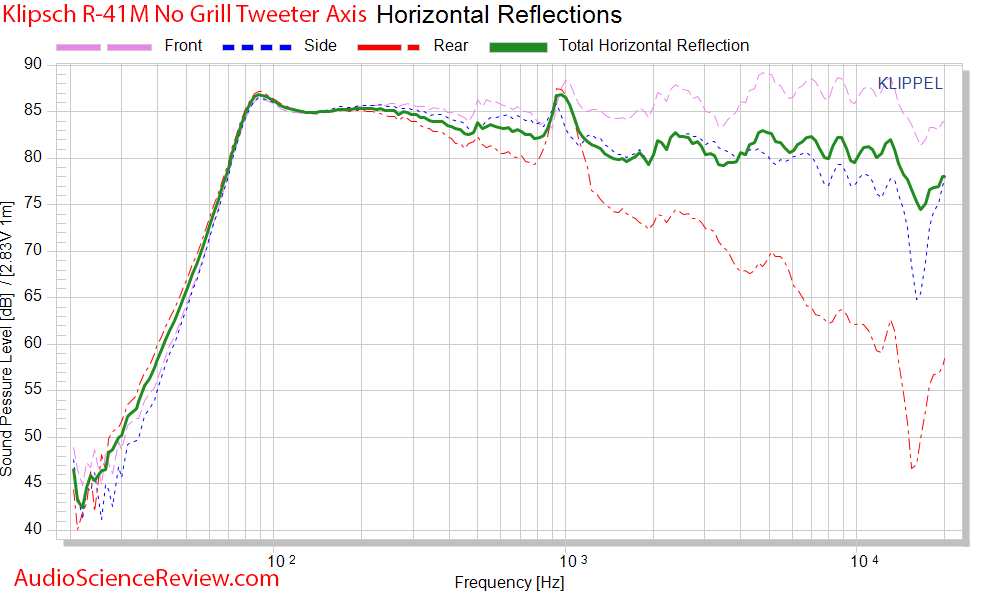
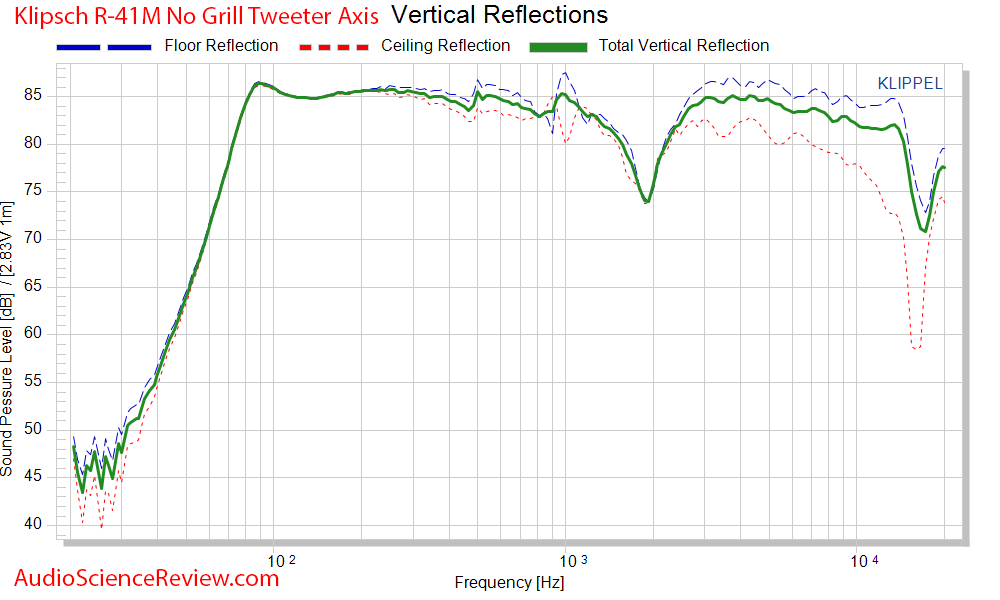
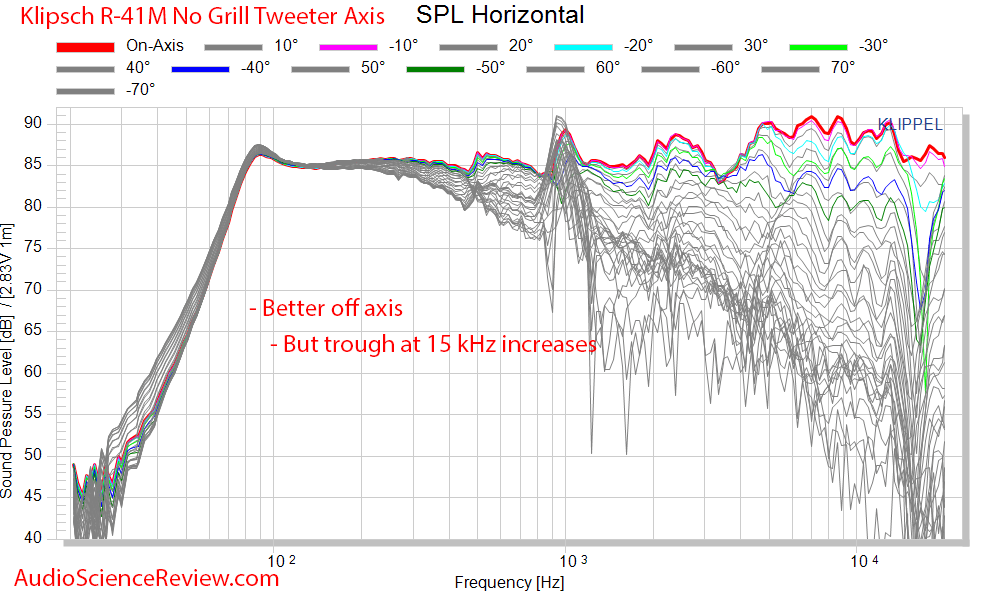
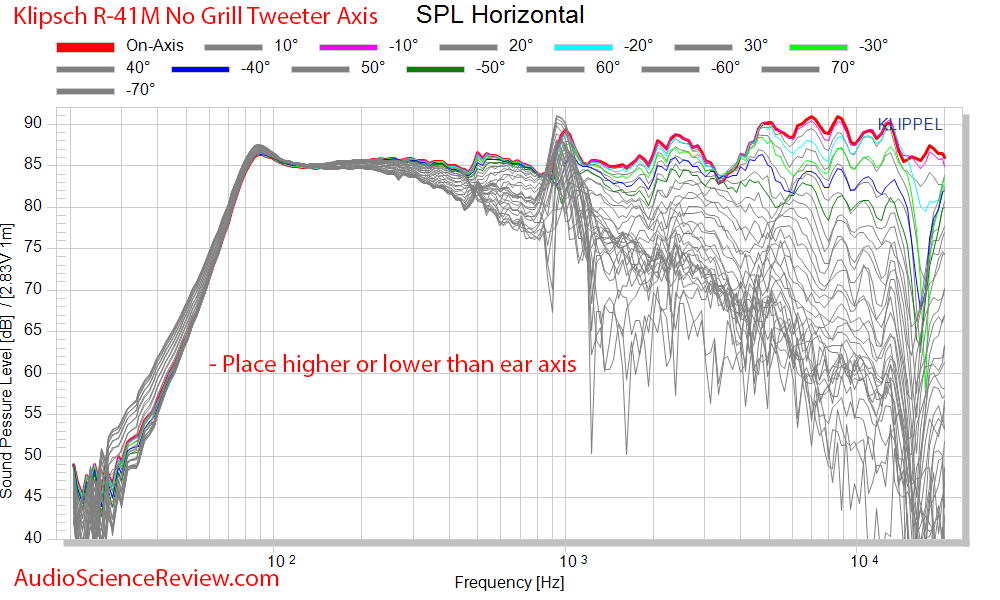
Eye-candy Speaker Measurements
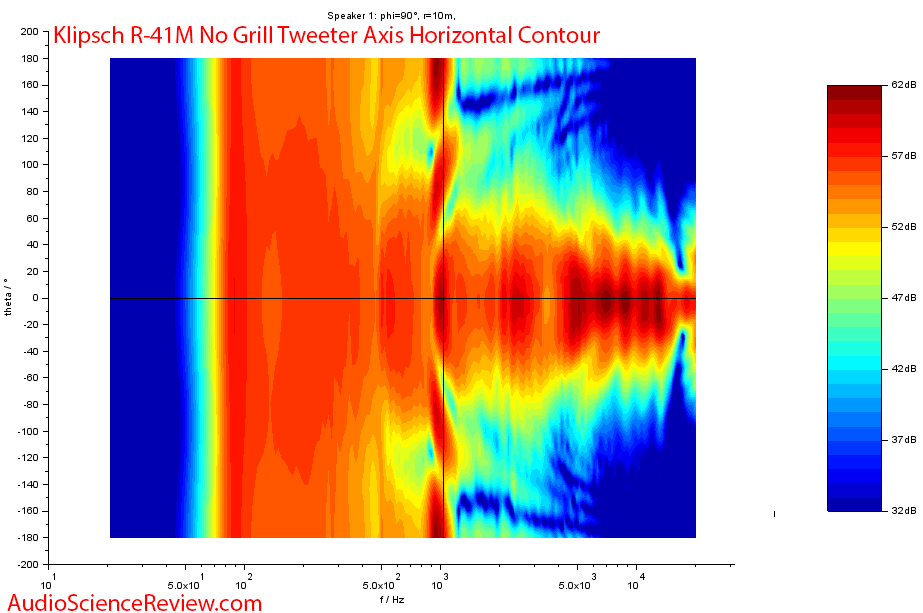
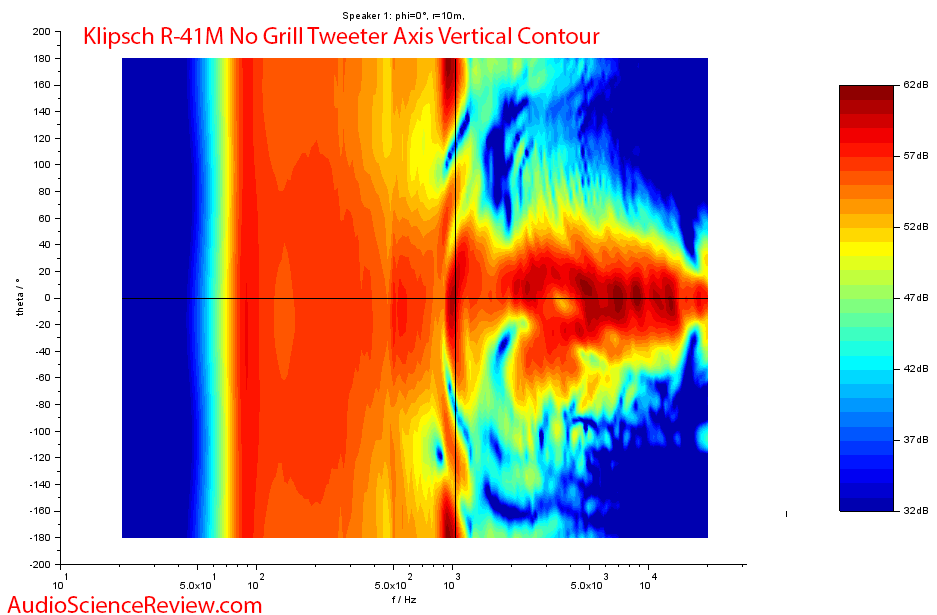
I went up to 18 kHz where only the tweeter is playing and got this wonderful confirmation of how well our instrumentation is working:

You can easily see the shape of the rectangular "horn."
Dropping down to 1 kHz where we had that peak shows some ugliness:

This is a side view. Can't figure out if this is some mixing of driver and its port of the sides singing along.
This is the kind of analysis that Klipsch should be doing, not us!
Speaker Listening Tests
Even though this is not a near-field monitor, I tested it that way. So shoot me!
On my right I had the Pioneer SP-BS22-LR and on the left the Klipsch R-41M. With levels matched and playing one channel at a time, the R-41M had no bass. It was all mid to highs. And boy, are those some highs. If you have not shaved, they are sharp enough to do that for you. I can see without a reference an inexperienced listener would instantly like them as "more clear, more detail, better imaging, etc." Switch to Pioneer though and you hear such a balance in tonality. Bass is there and overall sound is warm and pleasant. Not so with R-41M
Folks, I suffer with bad sound so you don't have to. Please avoid the Klipsch R-41M unless you just want a speaker as an ornament.
------------
As always, questions, comments, recommendations, etc. are welcome.
Finally having a few dry days so have to run out to fix our green house which got torn up with the winter storms. Have someone helping me which is good. Not so good is that I have to pay him at the end of the day. Would be good to have you all help with my other hobbies so please donate what you can using: https://www.audiosciencereview.com/forum/index.php?threads/how-to-support-audio-science-review.8150/
Have someone helping me which is good. Not so good is that I have to pay him at the end of the day. Would be good to have you all help with my other hobbies so please donate what you can using: https://www.audiosciencereview.com/forum/index.php?threads/how-to-support-audio-science-review.8150/
I always say speaker business is 80% marketing and Klipsch nails that with look and branding of this series of speakers:
You go into evaluation wanting it to sound good. After all, it even says it is "reference" quality speaker. Definitely a genius at work here.
The back panel sports nice (for the price) speaker terminals:
Hopefully the side panels are thicker than they look and the back panel is inset into them.
Measurements that you are about to see were performed using the Klippel Near-field Scanner (NFS). This is a robotic measurement system that analyzes the speaker all around and is able (using advanced mathematics and dual scan) to subtract room reflections. It also measures the speaker at close distance ("near-field") which sharply reduces the impact of room noise. Both of these factors enable testing in ordinary rooms yet results that can be more accurate than anechoic chamber. In a nutshell, the measurements show the actual sound coming out of the speaker independent of the room. All measurements are reference to tweeter axis with the grill removed.
Over 1000 points around the speaker were measured (from 20 to 20 kHz) which resulted in well under 1% error in identification of the sound field emanating from the speaker up to about 18 kHz. Above that the error increases slightly. Final database of measurements and data is 1.4 Gigabytes in size.
Spinorama Audio Measurements
Acoustic measurements can be grouped in a way that can be perceptually analyzed to determine how good a speaker can be used. This so called spinorama shows us just about everything we need to know about the speaker with respect to tonality and some flaws:
Boy, oh boy! Where to start. Let's start with that peak at 1 kHz. What on earth is that? It reminds me of Pinocchio's nose! I know Klipsch is known for bright highs but must we also throw in all those resonances as indicated by peaks that show up in all four upper graphs?
Since we fed the speaker 2.83 volts for measurements, the frequency response also becomes the sensitivity graph. We see that during much of the low spectrum were most of the music energy is, sensitivity is at 85 dB. It only gets to 90 dB during those terrible highs. So don't make the mistake of thinking this is an efficient speaker, it is not.
Direcitivty index graph needs to be smooth to allow us to fix the frequency response anomalies we see above but it is not:
Predicted in-room response fortunately is not as bad as on-axis:
The hotness of the tweeter wears off when not listened to on-axis, improving the response some. Still nothing to write home about unless you want this type of EQ applied to every piece of music you play. The people who incorrectly think everyone's taste in speakers is different can perhaps explain why some people may want every note around 1 kHz in their music to be exaggerated.
So we are done with how this speaker is going to "sound." It is going to sound very bright and uneven on-axis (speaker pointed at your ears). Toed out it will sound better but the measurements say avoid this speaker.
Basic Speaker Measurements
Impedance measurements show that the Klipsch spec of 8 ohms is a fantasy:
Response dips dangerously close to a short at 300 Hz or so. You better have a lot of amplification power there especially since sensitivity is low there as well.
There are a lot of kinks and such that indicate issues which I am not bothering to outline. They are also (potentially) visible in the waterfall measurements:
Then again we saw them so clearly in frequency response measurements including that 1 kHz peak.
Step function shows a kink as the tweet to woofer transition showing poor crossover design:
Continuing our low quality measurements we get to distortion:
Advanced Speaker Measurements
Eye-candy Speaker Measurements
I went up to 18 kHz where only the tweeter is playing and got this wonderful confirmation of how well our instrumentation is working:
You can easily see the shape of the rectangular "horn."
Dropping down to 1 kHz where we had that peak shows some ugliness:
This is a side view. Can't figure out if this is some mixing of driver and its port of the sides singing along.
This is the kind of analysis that Klipsch should be doing, not us!
Speaker Listening Tests
Even though this is not a near-field monitor, I tested it that way. So shoot me!
On my right I had the Pioneer SP-BS22-LR and on the left the Klipsch R-41M. With levels matched and playing one channel at a time, the R-41M had no bass. It was all mid to highs. And boy, are those some highs. If you have not shaved, they are sharp enough to do that for you. I can see without a reference an inexperienced listener would instantly like them as "more clear, more detail, better imaging, etc." Switch to Pioneer though and you hear such a balance in tonality. Bass is there and overall sound is warm and pleasant. Not so with R-41M
Folks, I suffer with bad sound so you don't have to. Please avoid the Klipsch R-41M unless you just want a speaker as an ornament.
------------
As always, questions, comments, recommendations, etc. are welcome.
Finally having a few dry days so have to run out to fix our green house which got torn up with the winter storms.
Last edited: