Device for Equal Loudness/Fletcher Munson Curve? Do Any Speakers Adapt to This?

[o2so]

ok, I get your point now,

first, it was never sugested that it creates perfect compensation.....for this the algorythm would have to be made for the specific listener ear anyways.

second, while not exactly true, the "spacing between the levels" are kind of linear.
the following is a graph of the ISO 226:2003 curves, relative to a reference level of 90dB (the flat uper border).
if you look at your 50Hz and the reference frequency of 1000Hz > let's say we have the 50Hz at 90dB and the 1000Hz at 80dB. now we attenuate 10dB via the algorythm. you get -6ish for 50Hz and -10dB for 1000Hz.
now if you do the same for a starting point with 50Hz at 84ish and 1000Hz at 90dB. now we attenuate 10dB via the algorythm. you get about 6ish for 50Hz again and -10dB for 1000Hz.

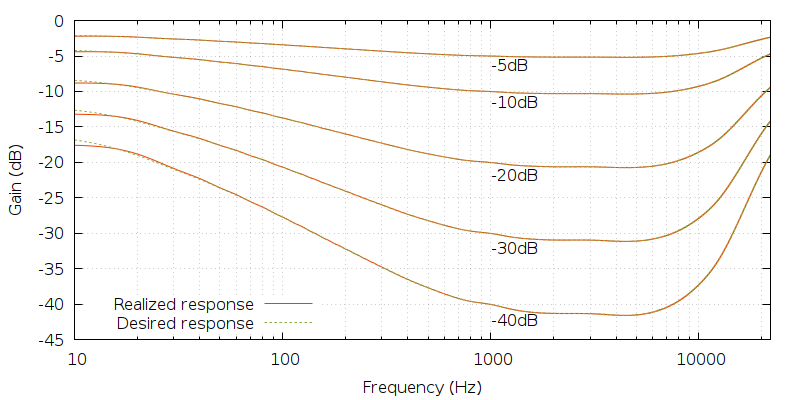
View attachment 100746

it obviously will never be perfect.....but it will be much better than hearing only half the music.


but hear for yourself: listen to Rebecca Pidgeon's rendition of Spanish Harlem -40dB below you reference level,
and then compare to this -40dB loudness compensated version (at your reference level): https://drive.google.com/file/d/11LjGW8E4Uqx4X17oKYvToJQrGTbzy-w9/view?usp=sharing

It has been a while since this post but I was wondering if you could share the exact source of the curves above. When I google ISO 226:2003 curves I get something different, that is:

ISO 226:2003 curves - Bing images

 

[dasdoing]

It has been a while since this post but I was wondering if you could share the exact source of the curves above. When I google ISO 226:2003 curves I get something different, that is:

ISO 226:2003 curves - Bing images

applying the ISO curves as a correction wont work.
note that at reference elevel you don't want any correction = flat curve
So in order to create a -40dB correction curve you need to subtract the 43dB curve from the 83dB curve.
the resuting correction curves look like this:

For the example I created I used this software: https://lsp-plug.in/?page=manuals&section=loud_comp_stereo

 

[o2so]

applying the ISO curves as a correction wont work.
note that at reference elevel you don't want any correction = flat curve
So in order to create a -40dB correction curve you need to subtract the 43dB curve from the 83dB curve.
the resuting correction curves look like this:

For the example I created I used this software: https://lsp-plug.in/?page=manuals&section=loud_comp_stereo

Thank you, very helpful. It works really well.

 

[dasdoing]

Thank you, very helpful. It works really well.

you're on Linux?

 

[j_j]

To get this right, you have to have full knowledge of what the listener is getting level-wise, and have signal-dependent, time-varying eq.

It can be done. It was done once. Amir even heard it. I have no idea wherefore it went.

 

[dasdoing]

To get this right, you have to have full knowledge of what the listener is getting level-wise, and have signal-dependent, time-varying eq.

It can be done. It was done once. Amir even heard it. I have no idea wherefore it went.

this was discussed in this topic.
loudness diferences in diferent music tracks is a problem that exists, equal-loudness corrected or not.

 

[gingerbeer]

moOde can do this too - basically the same approach that the RME ADI DAC used has been incorporated.

 

[o2so]

you're on Linux?

No, I am using the curve quite simply as a target curve in Dirac. I know that at night I listen at about 70db, so have used the relevant curve as target. It sounds very good to me, although I am still not sure I understand the reason of a different shape from the ISO curves. That is, why isn't the 83db curve flat in the ISO set of curves?

 

[dasdoing]

No, I am using the curve quite simply as a target curve in Dirac. I know that at night I listen at about 70db, so have used the relevant curve as target. It sounds very good to me, although I am still not sure I understand the reason of a different shape from the ISO curves. That is, why isn't the 83db curve flat in the ISO set of curves?

the iso curves are relative to 1000Hz. what they mean is for example at 83dB: a 1000Hz tone is meassured at 83dB. how loud must a 100Hz tone meassure to be percieved as the same loudness? do that for every frequency and you get to the curve.
Now, let's think of a recording of a natural sound with a perfectly flat microphone. in a perfectly flat speaker system you would reproduce the same sound with a flat curve at the exact same loudness level. If we play it back at a lower level then in nature we percieve the sound as unbalanced because a atenuation of let's say 10dB wont have the same perceptional atenuation at all frequenices.
enter equal-loudness correction: we continue using 1000Hz as a reference. we atenuated 1000Hz by 10dB (which is said to be "half the loudness"). how much do we have to atenuate 100Hz? at 1000Hz the diference is 10dB, but at 100Hz there is a smaller difference to percieve a half the loudness reduction. So we subtract the 10dB lower (at 1000Hz) curve from the original curve (reference) and get to our correction curve

 

[Chromatischism]

Audyssey's Dynamic EQ feature compensates for this. Ignore the levels on the left side. What you'll see is a shaping of the curve dependent on both frequency and master volume level.

Note that it does not exactly resemble the Fletcher + Munson curves in their extremity. I find you don't need quite as much as the raw research shows. The reasons for that likely include (my hypothesizing) some of it already "baked-in" by movie and music mastering engineers and room interactions lifting the bass naturally.

 

[o2so]

the iso curves are relative to 1000Hz. what they mean is for example at 83dB: a 1000Hz tone is meassured at 83dB. how loud must a 100Hz tone meassure to be percieved as the same loudness? do that for every frequency and you get to the curve.
Now, let's think of a recording of a natural sound with a perfectly flat microphone. in a perfectly flat speaker system you would reproduce the same sound with a flat curve at the exact same loudness level. If we play it back at a lower level then in nature we percieve the sound as unbalanced because a atenuation of let's say 10dB wont have the same perceptional atenuation at all frequenices.
enter equal-loudness correction: we continue using 1000Hz as a reference. we atenuated 1000Hz by 10dB (which is said to be "half the loudness"). how much do we have to atenuate 100Hz? at 1000Hz the diference is 10dB, but at 100Hz there is a smaller difference to percieve a half the loudness reduction. So we subtract the 10dB lower (at 1000Hz) curve from the original curve (reference) and get to our correction curve

I am probably dumb but still don't get it.
I don't expect you to give me a class so feel free to ignore this.
HOWEVER, I still cannot find an answer to my question. If our hearing is linear at 83db, why arent the ISO curves of equal loudness flat at 83db?

 

[j_j]

I am probably dumb but still don't get it.
I don't expect you to give me a class so feel free to ignore this.
HOWEVER, I still cannot find an answer to my question. If our hearing is linear at 83db, why arent the ISO curves of equal loudness flat at 83db?

Well, loudness is never precisely flat at any SPL. At low frequencies, the eardrum will always insert some highpass filtering. But your question says "linear" which is a different technical term altogether. I think you mean "loudness flat across frequency", but that's not linear. Linear says that the system obeys particular mathematical laws (which most do, more or less) but which has little to do with frequency. A rise or fall in frequency response can still happen in a linear system. I'm not trying to be pedantic here, but trying to sort out language.

 

[Chromatischism]

I am probably dumb but still don't get it.
I don't expect you to give me a class so feel free to ignore this.
HOWEVER, I still cannot find an answer to my question. If our hearing is linear at 83db, why arent the ISO curves of equal loudness flat at 83db?

Is there a source for that? It wouldn't be supported by Fletcher Munson and subsequent research, as you are noticing.

Besides, average loudness is all over the place in music recordings.

 

[o2so]

Well, loudness is never precisely flat at any SPL. At low frequencies, the eardrum will always insert some highpass filtering. But your question says "linear" which is a different technical term altogether. I think you mean "loudness flat across frequency", but that's not linear. Linear says that the system obeys particular mathematical laws (which most do, more or less) but which has little to do with frequency. A rise or fall in frequency response can still happen in a linear system. I'm not trying to be pedantic here, but trying to sort out language.

I interpreted linear as "measured response = perceived response" to our ears which probably does not make sense but this is how this term seems to be used in this context

 

[o2so]

Is there a source for that? It wouldn't be supported by Fletcher Munson and subsequent research, as you are noticing.

Besides, average loudness is all over the place in music recordings.

I have read this here and in many other forums but have not had time to verify accuracy or find a reference. Apparently, when you listen at 83db it is ok to have a flat-ish frequency response. If you listen at lower levels, then you need to compensate for equal loudness. or not?

 

[o2so]

Ahhhhhhhh got it.

at 83db our perceived frequency response is not flat, HOWEVER this is the reference level at which most recordings are mastered. These are already compensated by the engineer to sound balanced (according to his ears) when replayed at 83db (with a system producing a flat response). Hence why one has to subtract the ISO curves to adjust for replay levels below 83db. All makes sense now

 

[TimoJ]

Ahhhhhhhh got it.

at 83db our perceived frequency response is not flat, HOWEVER this is the reference level at which most recordings are mastered. These are already compensated by the engineer to sound balanced (according to his ears) when replayed at 83db (with a system producing a flat response). Hence why one has to subtract the ISO curves to adjust for replay levels below 83db. All makes sense now

Except mastering isn't done with identical in-room responses, so it's pretty hopeless, read the link below. Just adjust sound to your liking (for each record) and that's it.
Audio Musings by Sean Olive: Audio's Circle of Confusion

 

[o2so]

Except mastering isn't done with identical in-room responses, so it's pretty hopeless, read the link below. Just adjust sound to your liking (for each record) and that's it.
Audio Musings by Sean Olive: Audio's Circle of Confusion

I am not sure how common the issue of mastering room responses is and the extent to which it would affect the master. It certainly will to some extent but I would have thought that most mastering studios are well organized to produce a flattish response in the nearfield. It wont be perfect ok, but using the equal loudness filters above as target curves in Dirac I am having very pleasant results with a range of recordings.

 

[Music1969]

applying the ISO curves as a correction wont work.
note that at reference elevel you don't want any correction = flat curve
So in order to create a -40dB correction curve you need to subtract the 43dB curve from the 83dB curve.
the resuting correction curves look like this:

For the example I created I used this software: https://lsp-plug.in/?page=manuals&section=loud_comp_stereo

Hi, does anyone have the raw data plots for these curves?

In text file is ok. Something that can be imported into REW

 

[o2so]

Well, loudness is never precisely flat at any SPL. At low frequencies, the eardrum will always insert some highpass filtering. But your question says "linear" which is a different technical term altogether. I think you mean "loudness flat across frequency", but that's not linear. Linear says that the system obeys particular mathematical laws (which most do, more or less) but which has little to do with frequency. A rise or fall in frequency response can still happen in a linear system. I'm not trying to be pedantic here, but trying to sort out language.

Hi again, and quick question. What weighting type should I use when measuring my SPL so I can apply the correct correction curve? In other words, what weighting type are the ISO curves based on? A, C or Z? I find that there is a lot of difference in the readings when changing weighting type. I think it should be C or Z but just checking.

Also, do the adjustment EQ curves refer to the average SPL or to the peak? I read in some of Bob Katz's comments that 83db is only for the "forte" passages.