Hi
Here are some measurements of the new RME UCX II Interface
Please apologize if there is any error here.
Don't hesitate to ask or flag in case of doubt.
The RME UCX II is a new small USB interface from RME, belonging to the UFX II and UFX+ family.
Its small size (1/2 rack wide and 1U high) is the same than the RME ADI-2 Pro fs R that I use for measurements.
The purpose is very different, though.
You see both on this picture.
The UCX II is on top.

This is a powerful small interface, if limited in number of IOs:
USB, of course,
2 Microphone inputs, 2 instrument inputs, 4 line inputs,
6 line outputs and 1 stereo Headphones output
There are also connectors for MIDI In and Out, a configurable WordClock connector, ADAT in and out, and a USB DuRec slot.

It also has AES/EBU + SPDIF in and out connectors through the use of this adaptor that plugs on the rear DB9.
The same than the one used for the RME ADI-2 Pro fs R.

Power supply is the same lockable 12V DC 2A external that we find with the ADI-2 Pro fs R.
That of course means that it's possible to run the device on a 12V battery.
A very positive point in this case.

Functionalities
This is a powerful little interface
I invite you to read and look at tutorial videos
As usual with RME, the drivers on Windows are very stable.
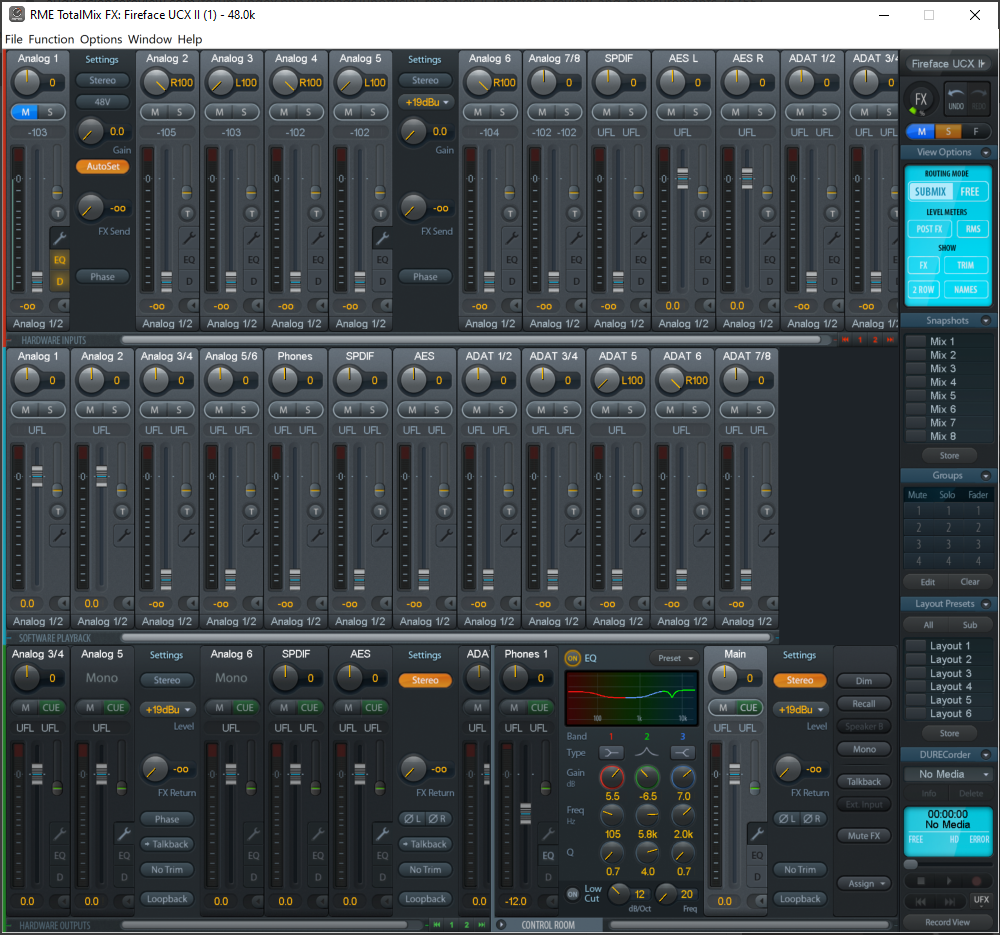
And the (provided) Totalmix application is really easy to use.
So there is much more in there than just good measurements.
Measurements
I always perform my measurements using Virtins MultiInstrument 3.9 and some .Net application and SQL database of mines.
I own a license of MI.
The hardware consists of the RME ADI-2 Pro fs R.
A positively incredible device, with state-of-the-art performances, both for ADC and DAC.
Unless specified, I measure using the ADI-2 in "mono" mode, to benefit of a slightly increased performance, by summing (averaging) the 2 ADC or DAC channels.
I purchased the RME UCX II from a French shop.
DAC side measurements
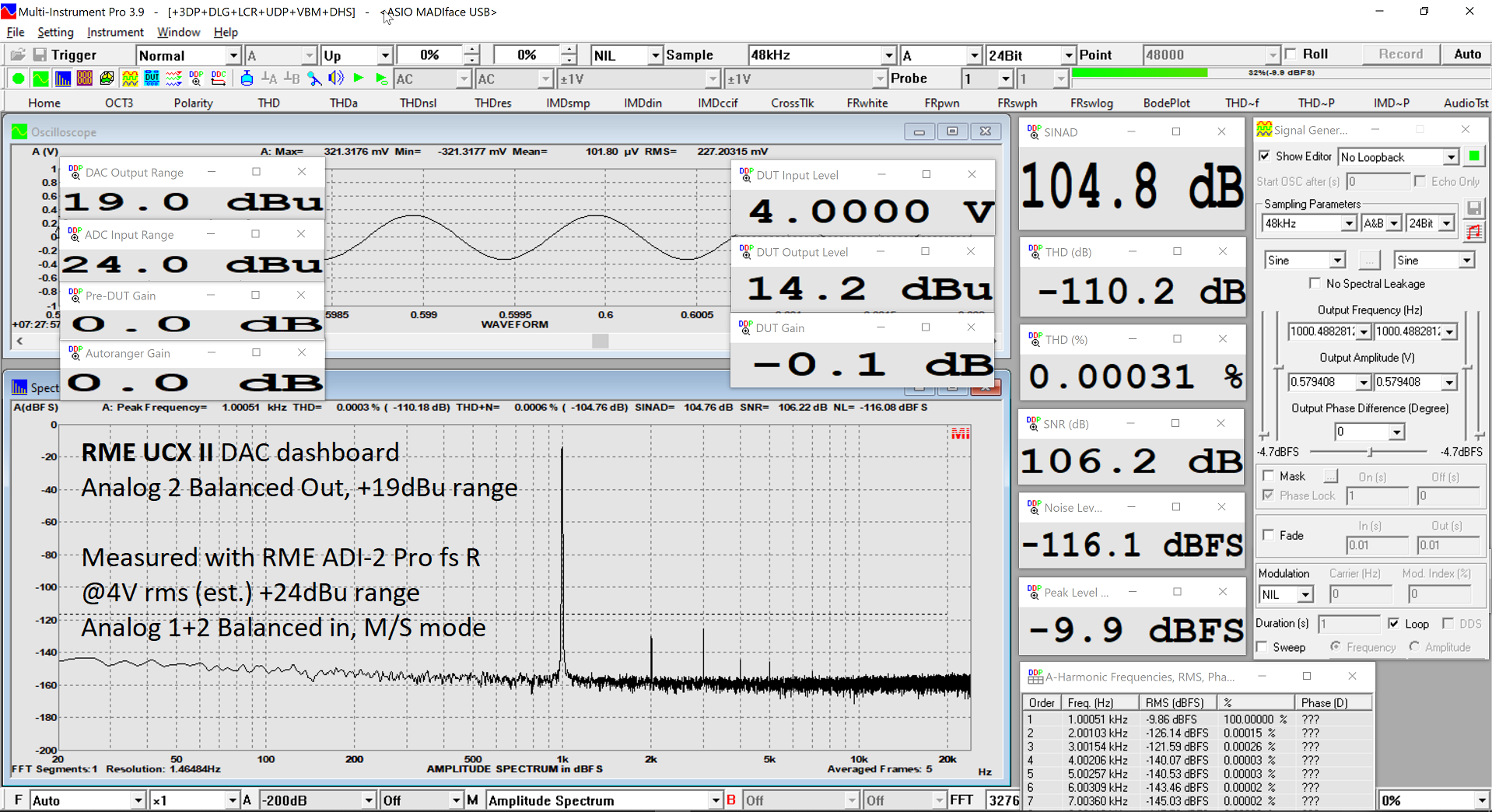
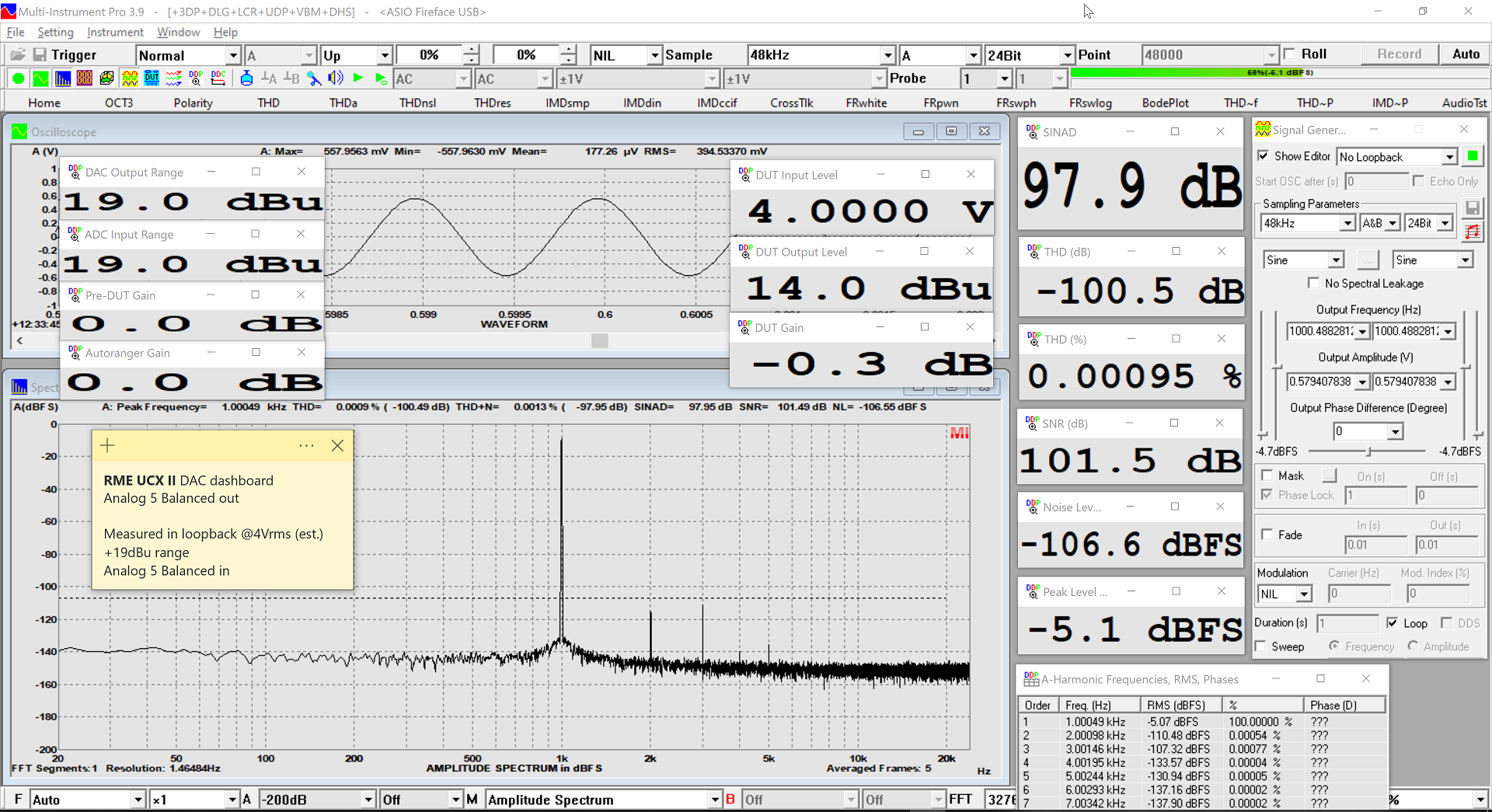
Dashboard 4Vrms (48kHz)
We get a SINAD just shy of 105dB.
Not state of the art, but good enough for the usecase. And in line with the specs.
(NB: Voltage is not measured, but computed from 19dBu)
EDIT: I remeasured and updated with ADC range of +24dBu, which gives better result.
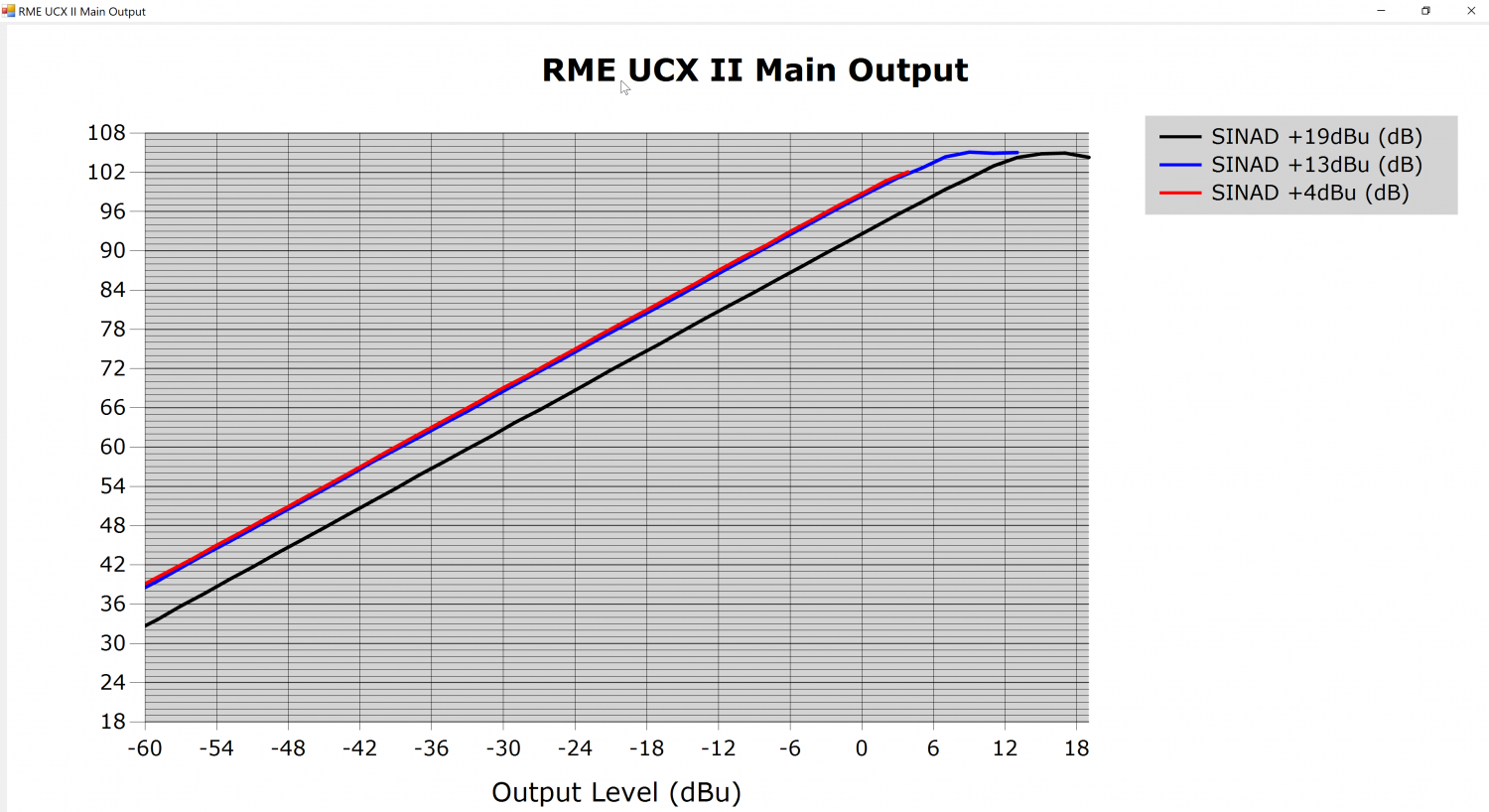
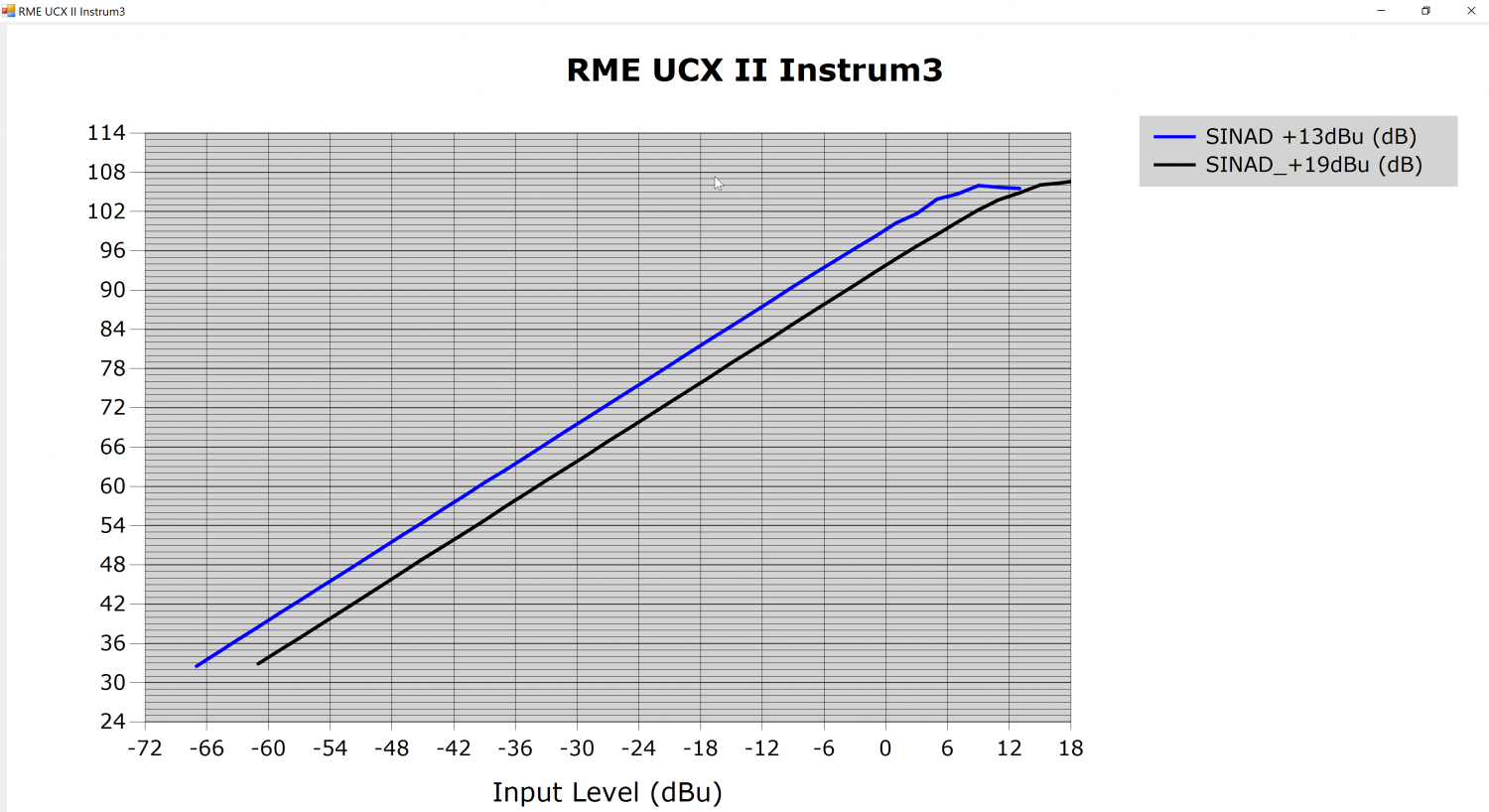
I plotted SINAD vs Level for the 3 available output ranges
It is noticeable that the +4dBu is in fact exactly matching the +13dBu curve.
This most probably means that the +4dBu range is provided for convenience only, by limiting the level in digital domain.
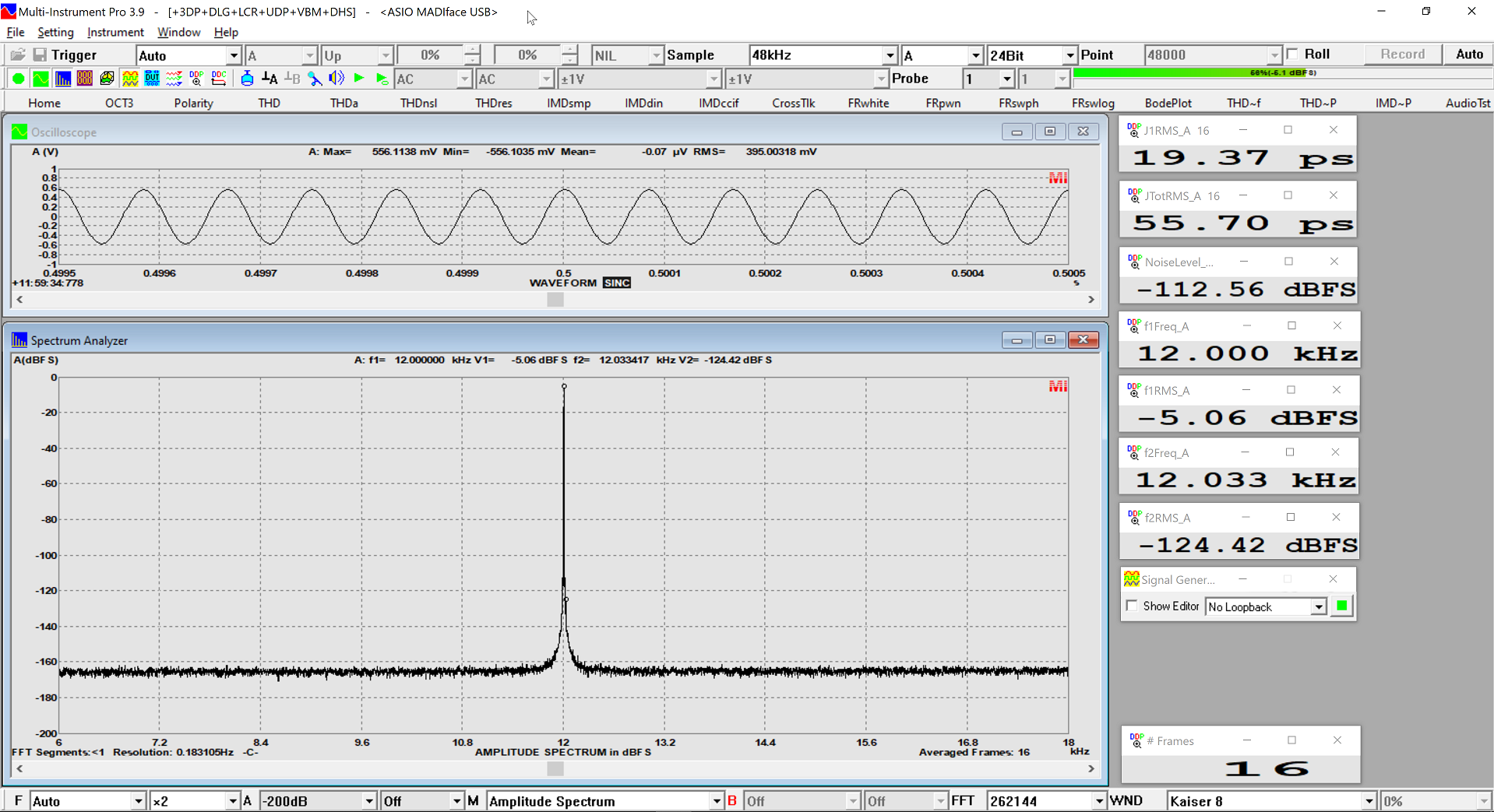
Jitter
(Source = USB, but we get exactly the same measurement from AES)
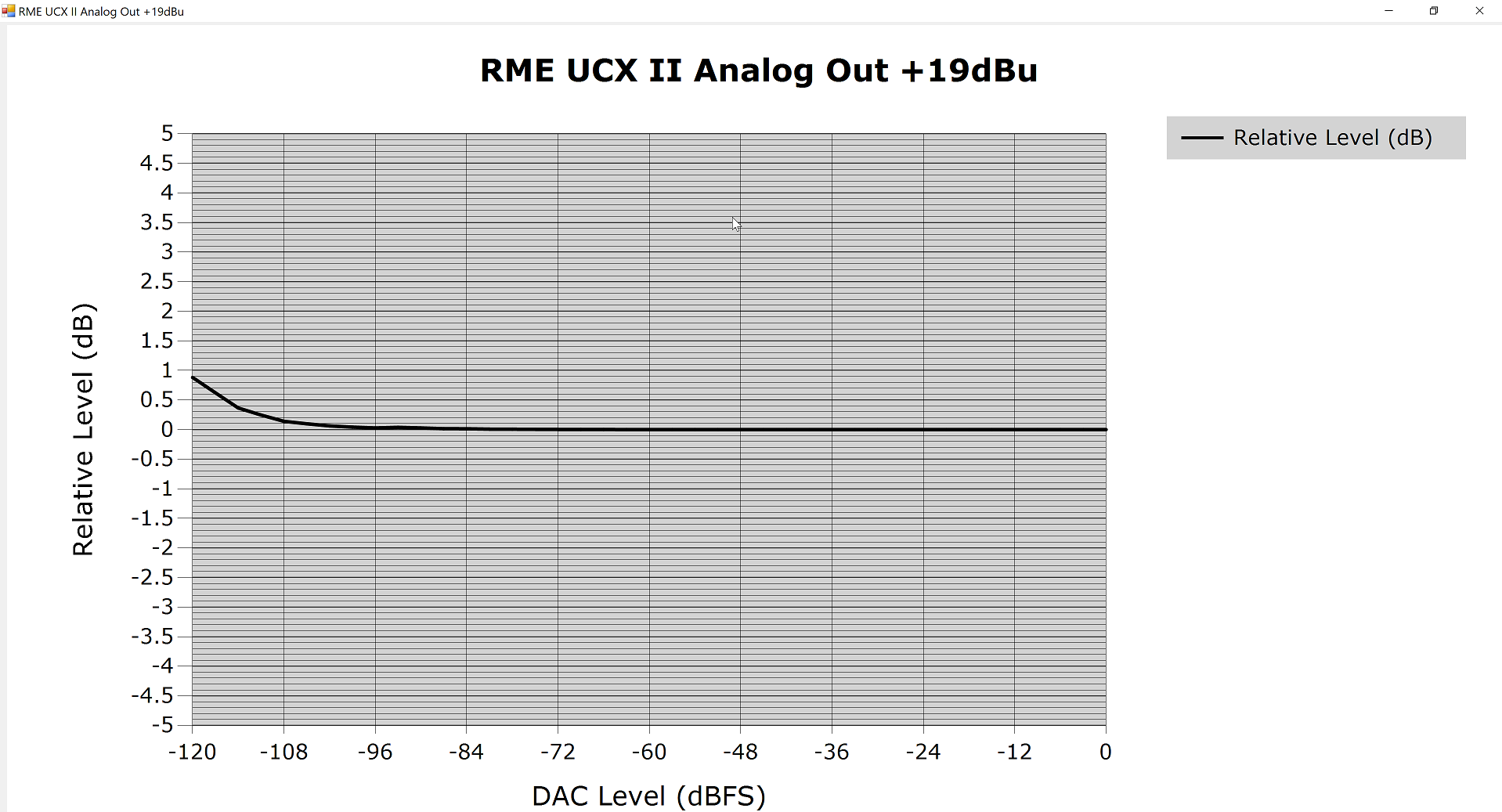
Level Linearity
Nothing to worry about
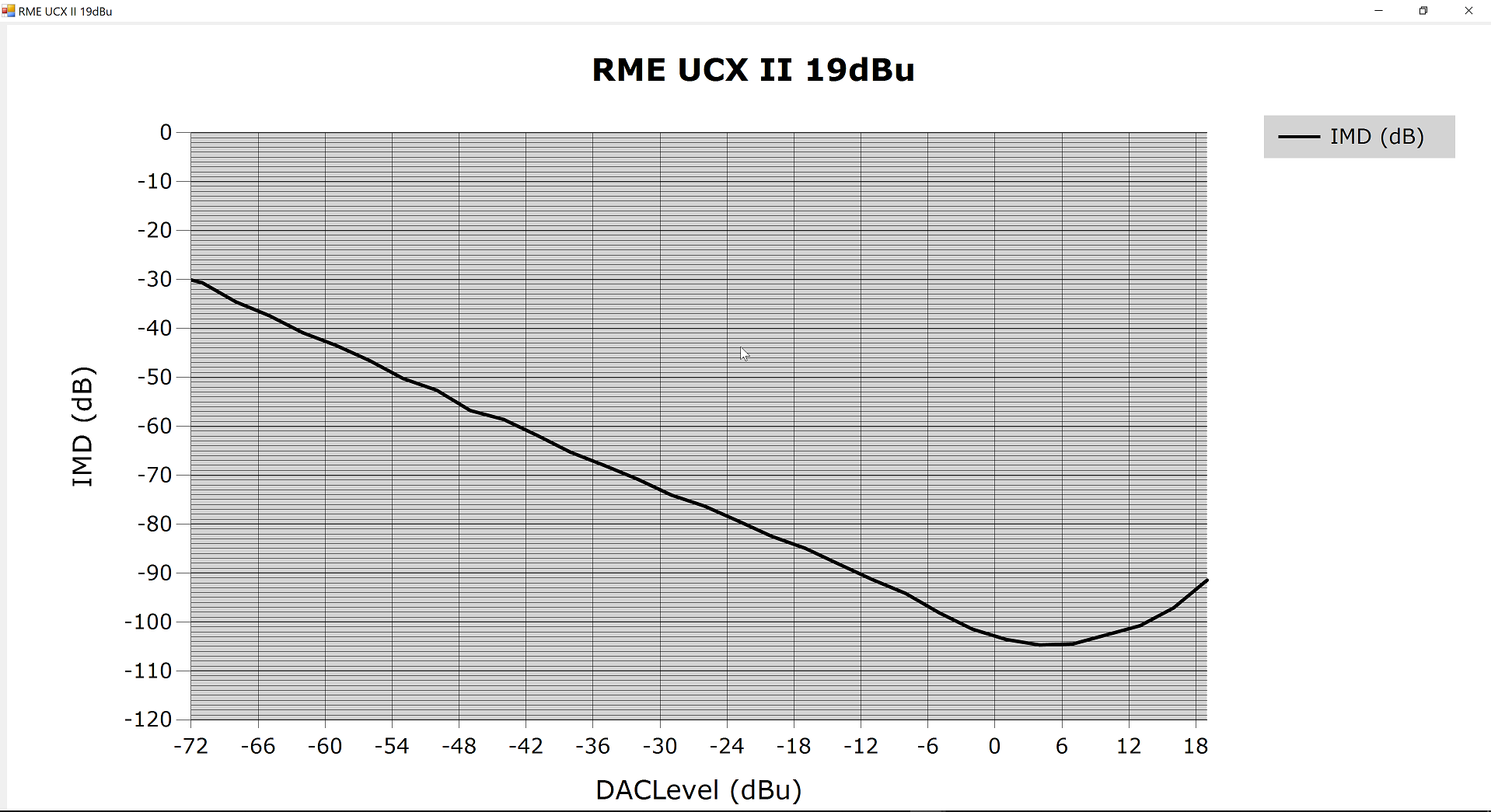
IMD vs Level
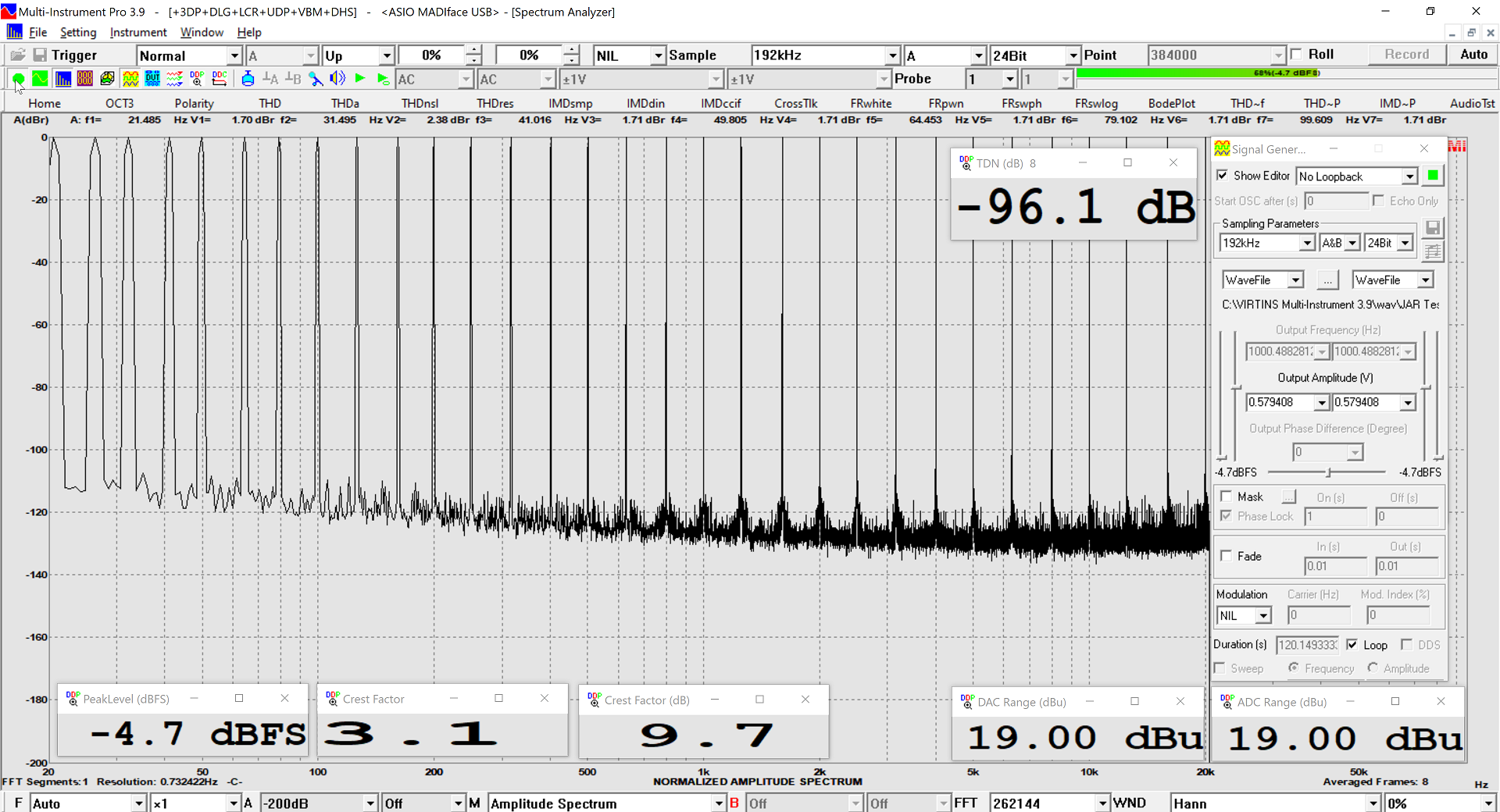
32 tones
No issue
This is using Amir's APx555 test file
32nd tone isn't displayed, since it's at 14Hz
EDIT: I now use the WAV file (better crest factor), another FFT Window function, 8 averages and proper 192kHz frequency and 256k points to align with Amir's 32 tones.
Filter @48kHz
EDIT: I re-measured this one after @MC_RME's comment. My original plot was using wong windowing.
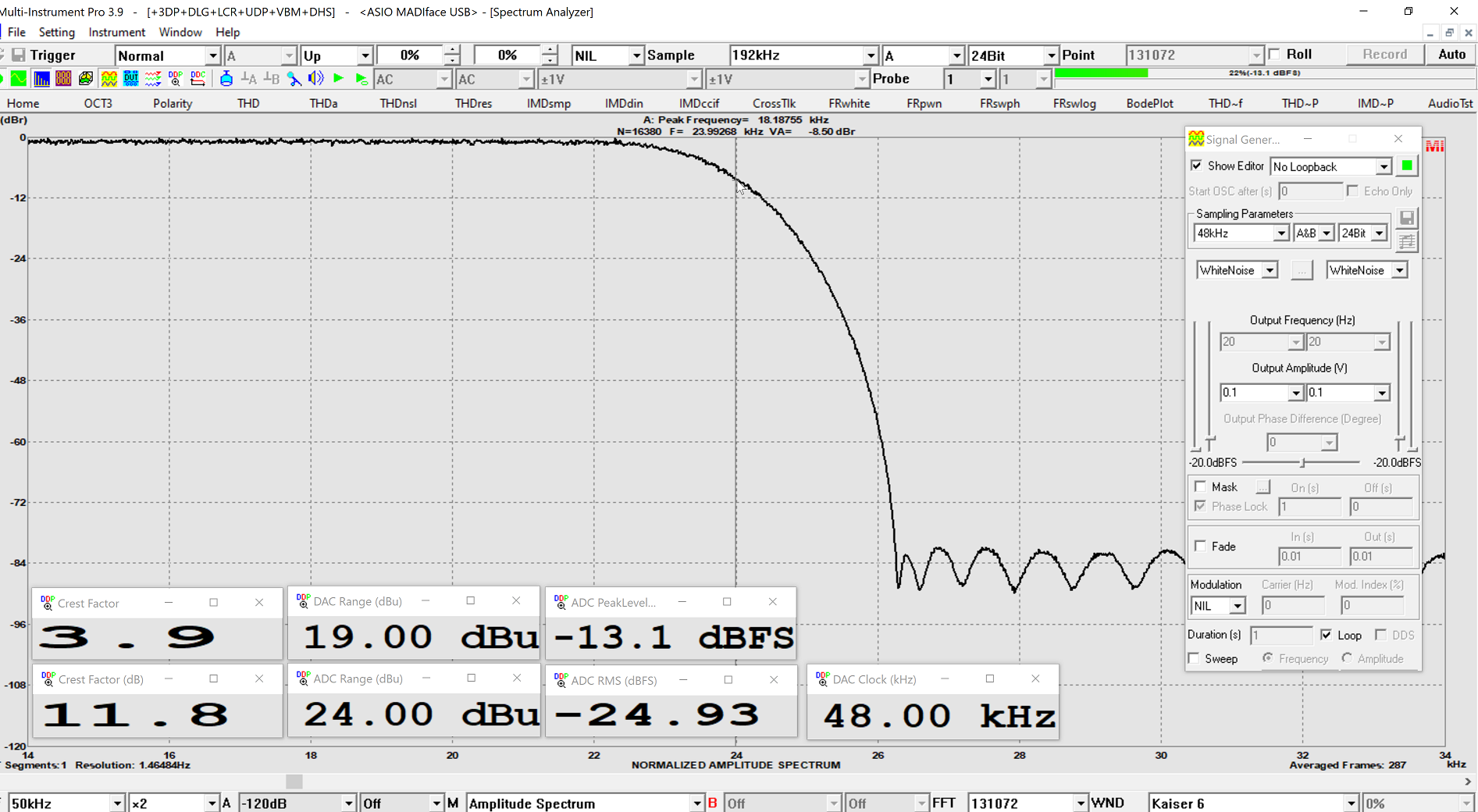
NB: This is a measurement I wanted to achieve for a long time but could never have to work.
Here it does, since the ADI-2 and UCX II have 2 different drivers. And MultiInstrument then allows to set a different clock for each device for a measurement.
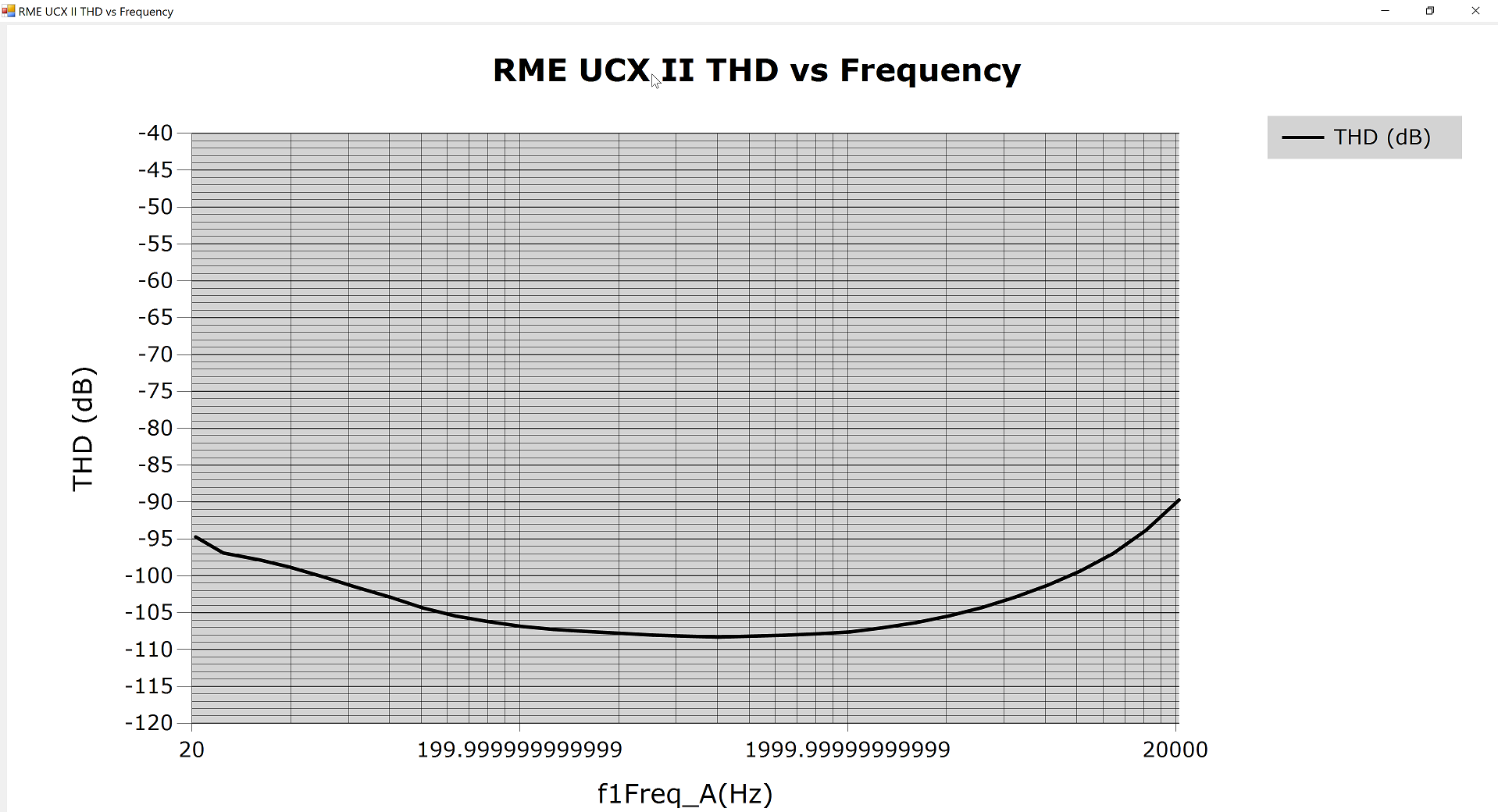
THD vs Frequency @4Vrms (90kHz BW)
EDIT: At first, I had higher values and some strange peaks at low frequencies.
I now limit the number of harmonics to 5.
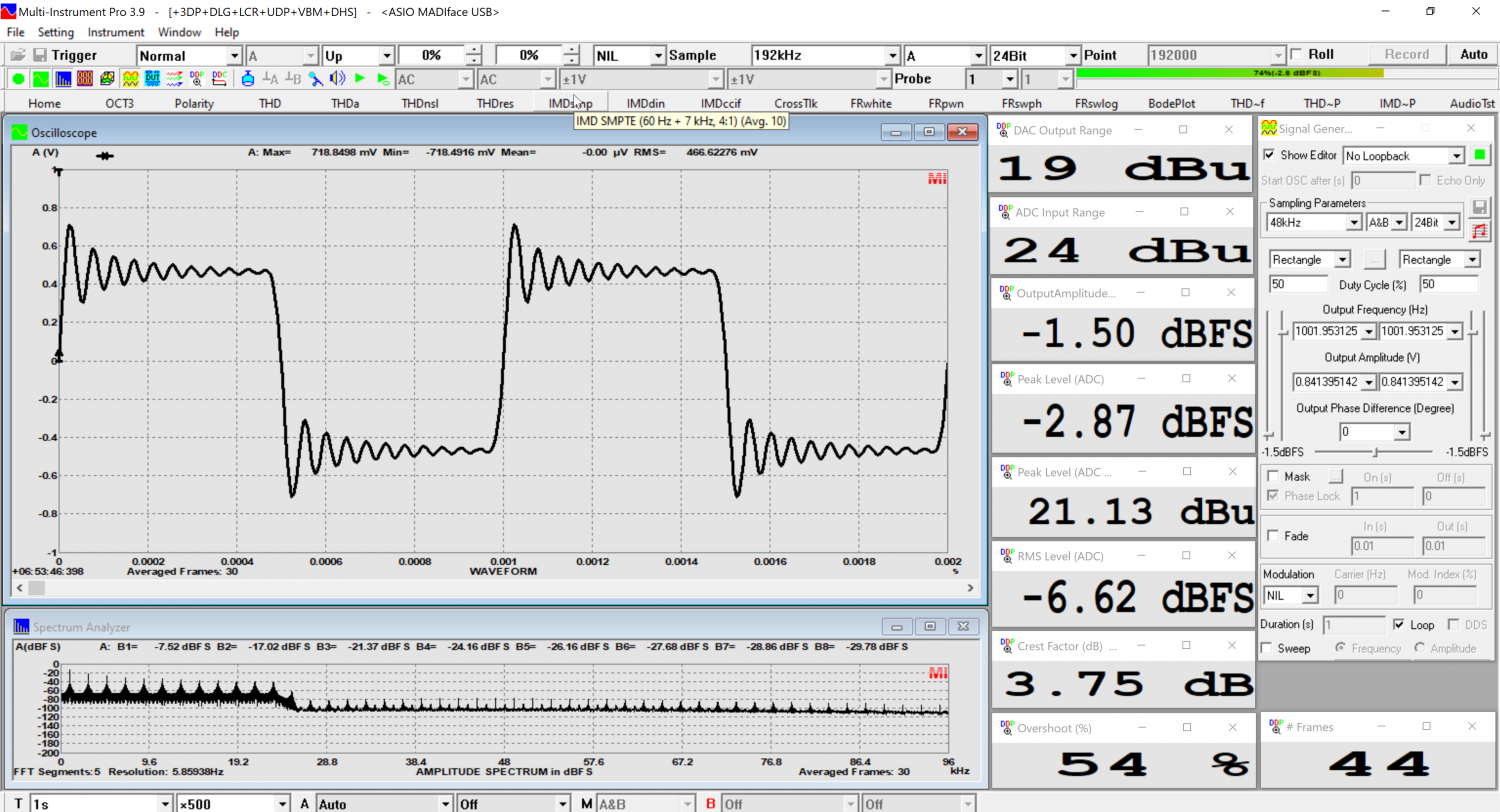
Square wave
I've run some more analysis on this.
Warning: as you can read below, I'm mostly experimenting here, so don't attach too much importance to this measurement
At low level, here is what the 1kHz square wave looks like
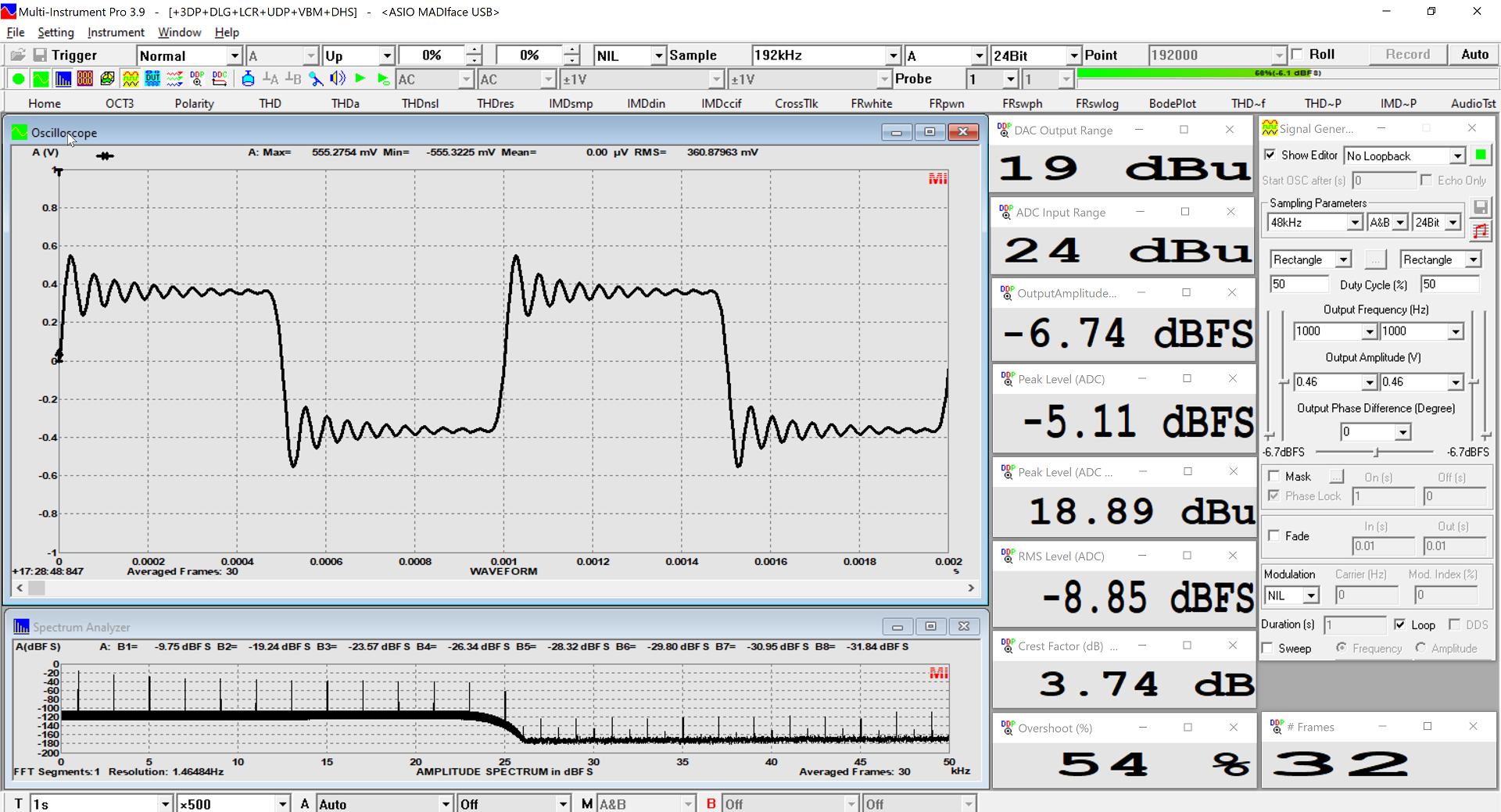
But if we run it at 0dBFS, it is somehow truncated
We see a reduction of 1.5dB of the Crest factor
Not too bad, though. Most interfaces are probably worse.
EDIT: Actually, the level reaching the ADC is higher than the output range of the DAC by almost 2dB, at 20.9dBu.
This is what I wanted to demonstrate.
(This is a torture test. Nothing looks like a square wave in real life)
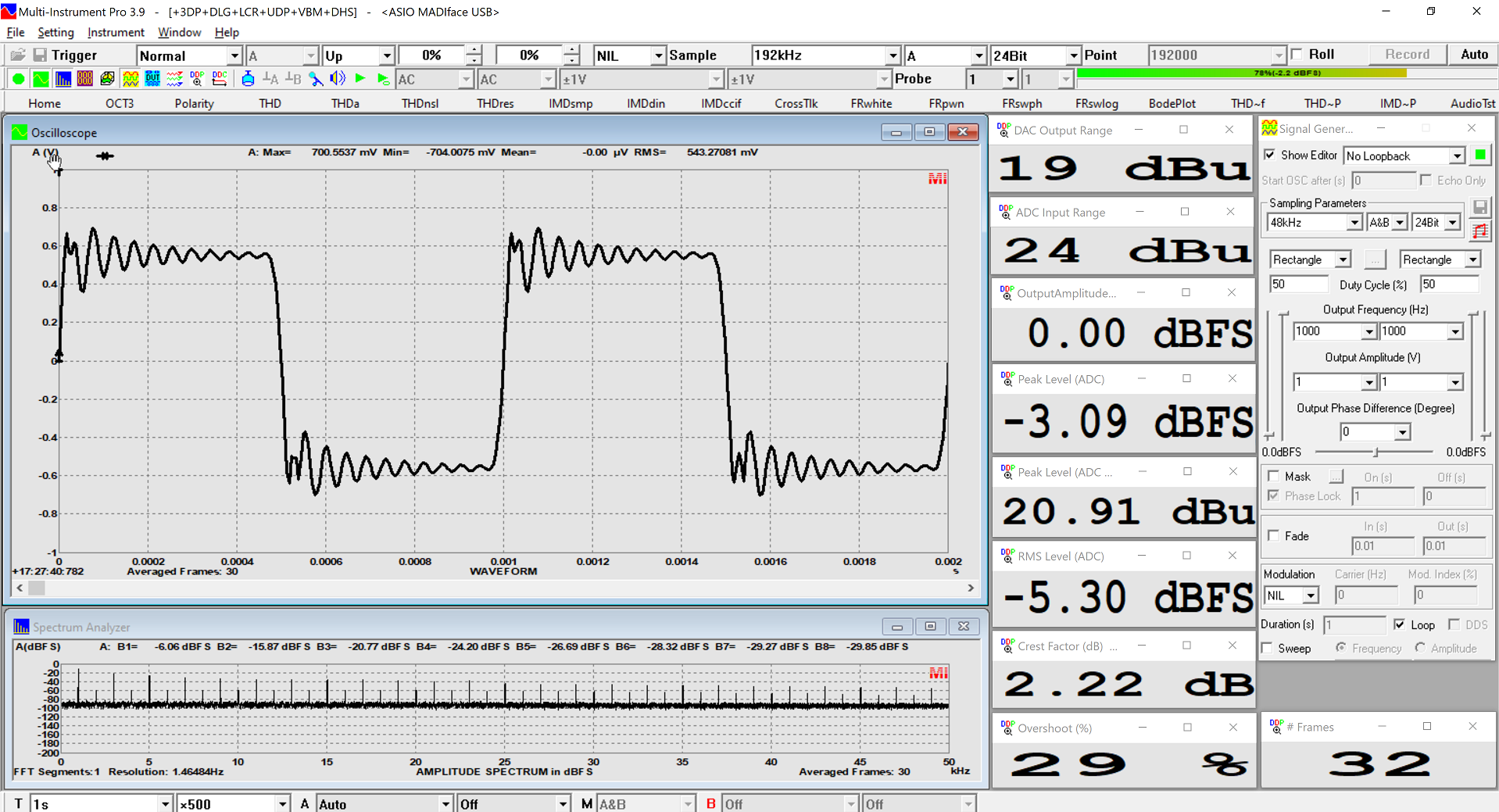
As from -1.5dBFS, there is no more truncation (Edited. See below)
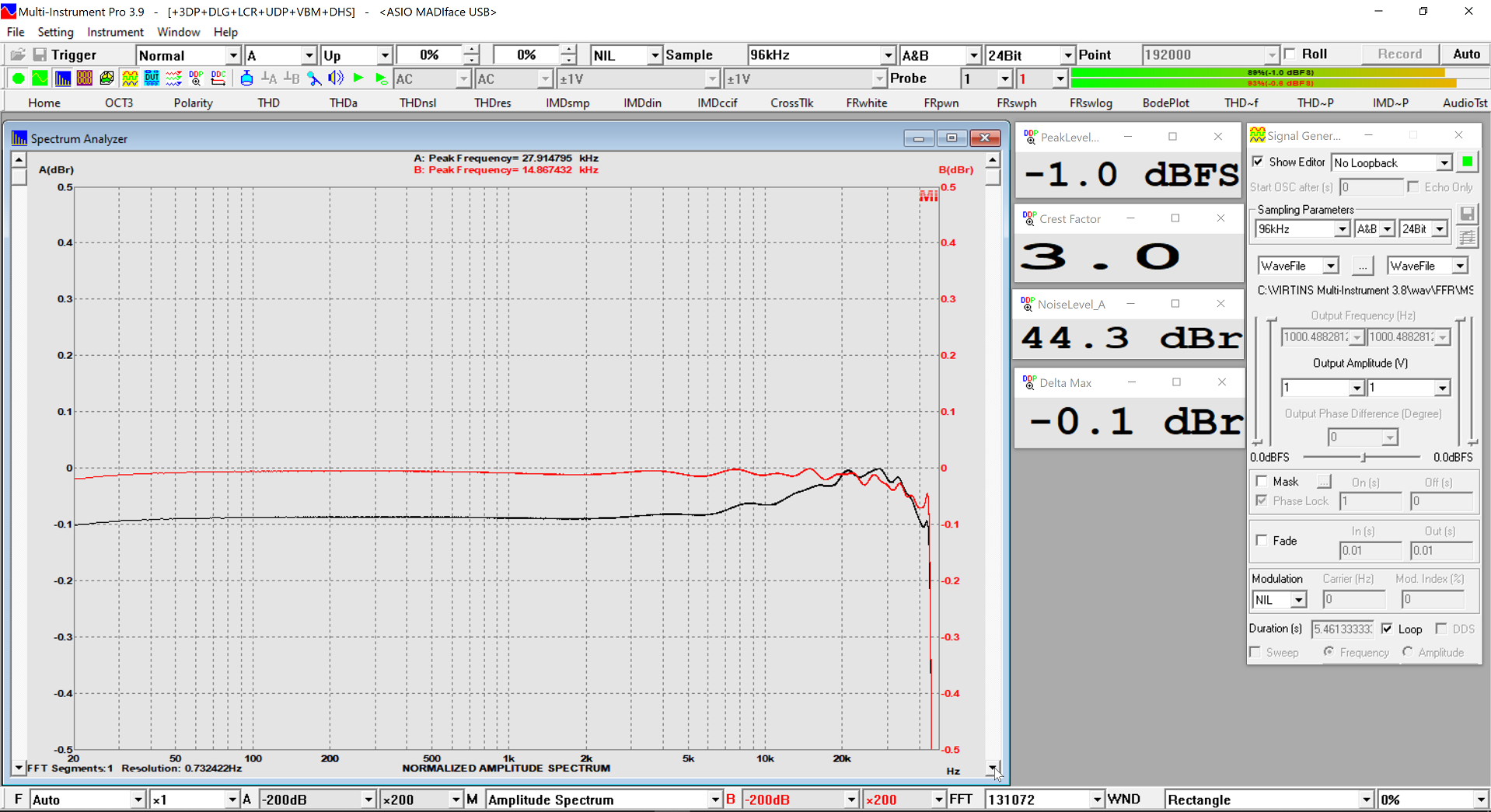
Frequency response à 96kHz
Here in 13dBu range. 19dBu is identical
For reference, the RME ADI-2 Pro fs R is plotted in red, since its ADC is not completely flat at that frequency.
... ADC measurements will come later
As an appetizer, here is the
SINAD plot for Instrument input
and here is the
Dashboard @4V in Loopback mode
(DAC + ADC = RME UCX II)
We clear more than required CD SINAD for the loopback.
Good news if you want to insert an external analog effect, which will most likely perform much worse than this.
(In attachments, you may still find the plots that I updated, for reference)
Here are some measurements of the new RME UCX II Interface
Please apologize if there is any error here.
Don't hesitate to ask or flag in case of doubt.
The RME UCX II is a new small USB interface from RME, belonging to the UFX II and UFX+ family.
Its small size (1/2 rack wide and 1U high) is the same than the RME ADI-2 Pro fs R that I use for measurements.
The purpose is very different, though.
You see both on this picture.
The UCX II is on top.
This is a powerful small interface, if limited in number of IOs:
USB, of course,
2 Microphone inputs, 2 instrument inputs, 4 line inputs,
6 line outputs and 1 stereo Headphones output
There are also connectors for MIDI In and Out, a configurable WordClock connector, ADAT in and out, and a USB DuRec slot.
It also has AES/EBU + SPDIF in and out connectors through the use of this adaptor that plugs on the rear DB9.
The same than the one used for the RME ADI-2 Pro fs R.
Power supply is the same lockable 12V DC 2A external that we find with the ADI-2 Pro fs R.
That of course means that it's possible to run the device on a 12V battery.
A very positive point in this case.
Functionalities
This is a powerful little interface
I invite you to read and look at tutorial videos
As usual with RME, the drivers on Windows are very stable.
And the (provided) Totalmix application is really easy to use.
So there is much more in there than just good measurements.
Measurements
I always perform my measurements using Virtins MultiInstrument 3.9 and some .Net application and SQL database of mines.
I own a license of MI.
The hardware consists of the RME ADI-2 Pro fs R.
A positively incredible device, with state-of-the-art performances, both for ADC and DAC.
Unless specified, I measure using the ADI-2 in "mono" mode, to benefit of a slightly increased performance, by summing (averaging) the 2 ADC or DAC channels.
I purchased the RME UCX II from a French shop.
DAC side measurements
Dashboard 4Vrms (48kHz)
We get a SINAD just shy of 105dB.
Not state of the art, but good enough for the usecase. And in line with the specs.
(NB: Voltage is not measured, but computed from 19dBu)
EDIT: I remeasured and updated with ADC range of +24dBu, which gives better result.
I plotted SINAD vs Level for the 3 available output ranges
It is noticeable that the +4dBu is in fact exactly matching the +13dBu curve.
This most probably means that the +4dBu range is provided for convenience only, by limiting the level in digital domain.
Jitter
(Source = USB, but we get exactly the same measurement from AES)
Level Linearity
Nothing to worry about
IMD vs Level
32 tones
No issue
This is using Amir's APx555 test file
32nd tone isn't displayed, since it's at 14Hz
EDIT: I now use the WAV file (better crest factor), another FFT Window function, 8 averages and proper 192kHz frequency and 256k points to align with Amir's 32 tones.
Filter @48kHz
EDIT: I re-measured this one after @MC_RME's comment. My original plot was using wong windowing.
NB: This is a measurement I wanted to achieve for a long time but could never have to work.
Here it does, since the ADI-2 and UCX II have 2 different drivers. And MultiInstrument then allows to set a different clock for each device for a measurement.
THD vs Frequency @4Vrms (90kHz BW)
EDIT: At first, I had higher values and some strange peaks at low frequencies.
I now limit the number of harmonics to 5.
Square wave
I've run some more analysis on this.
Warning: as you can read below, I'm mostly experimenting here, so don't attach too much importance to this measurement
At low level, here is what the 1kHz square wave looks like
But if we run it at 0dBFS, it is somehow truncated
We see a reduction of 1.5dB of the Crest factor
Not too bad, though. Most interfaces are probably worse.
EDIT: Actually, the level reaching the ADC is higher than the output range of the DAC by almost 2dB, at 20.9dBu.
This is what I wanted to demonstrate.
(This is a torture test. Nothing looks like a square wave in real life)
As from -1.5dBFS, there is no more truncation (Edited. See below)
Frequency response à 96kHz
Here in 13dBu range. 19dBu is identical
For reference, the RME ADI-2 Pro fs R is plotted in red, since its ADC is not completely flat at that frequency.
... ADC measurements will come later
As an appetizer, here is the
SINAD plot for Instrument input
and here is the
Dashboard @4V in Loopback mode
(DAC + ADC = RME UCX II)
We clear more than required CD SINAD for the loopback.
Good news if you want to insert an external analog effect, which will most likely perform much worse than this.
(In attachments, you may still find the plots that I updated, for reference)
Attachments
Last edited: