THD Measurement: Do it represent the actual nonlinear harmonic distortion?

[mansr]

I was strictly commenting on @mansr statement: "any change to the fundamental is a linear distortion" which is, in general, IMO incorrect (or wrongly formulated).

I guess I should have included the word "static" there. That said, any nonlinear system will introduce additional frequency components, though not necessarily harmonics.

 

[pkane]

So, the answer to the question in the thread title, if THD represents the nonlinear distortion of a system, would be a nice NO.

[EDIT] You must admit that this difference is very fine. The non-linearities of a system generate harmonic distortions. I measure the energy level of these distortions but, since in some cases some of them escape, I cannot attribute this measure as a indicator of the non-linearities present in my device. But this association is what people commonly do and expect… The difference should be explained to them, since it would be necessary to correct the calculation of the THD and IMD to make them representative, or to prepare new, more sophisticated metrics.

There may be a somewhat practical reason to neglect changes to the fundamental. For one, the energy from the fundamental is distributed into the harmonics/IMD products, lowering its amplitude. Any increase due to the nonlinearity will be offset to some degree by this energy loss due to the harmonics. What's more, a small increase or decrease in the level of the fundamental is much less likely to be audible than the harmonic/IMD products due to masking. Not saying it's not interesting to see the effect and how much it contributes, but there are good reasons to ignore it. That said, can you provide a real-life example showing the change in amplitude of the fundamental due to HD1 (not a simulated result)?

 

[Pinox67]

How about 3D to catch fluctuations of H1 and harmonic and non-harmonic distortion components?

You can follow the procedure below to estimate HD1:

1. Insert a single tone at different frequencies (e.g. 32Hz, 63Hz, 125Hz, 250Hz, … 16KHz) into your device, and measure all harmonic distortions, in magnitude and phase.

2. Check the applicability of the static (memory-less) model:

• The values of magnitude and phase must be almost constant for all tones.
• By changing the signal level, the phases of the harmonics have negligible (few degrees) changes.
• The phases of the harmonics must be close (let's say ±15 degrees) to the values in Tab. 2a or 2b (or the same with ±180 degrees) of this post.

3. If all previous tests are passed:

• Write a linear system of equations, as described in the first paragraph of the same post; solve it and you will obtain the coefficients ai of the polynomial that models the transfer function.
• Using Tab. 1b it is possible to obtain HD1 (coefficients in the first column) and carry out the verification with the values of the other HDi values.

If the conditions described at step 2 are not verified, see the evolution for dynamic systems in the post #46.

 

[syn08]

I guess I should have included the word "static" there. That said, any nonlinear system will introduce additional frequency components, though not necessarily harmonics.

This is still incorrect; a time invariant non linear system will create only harmonic components. The concept of "inharmonic distortions" was many time wrongly invoked by the pseudo audio experts, to justify that THD, as computed per definition, is an incomplete metric for the system nonlinearity.

 

[pma]

That said, can you provide a real-life example showing the change in amplitude of the fundamental due to HD1 (not a simulated result)?

Tube amplifier, as shown in post #17.

 

[Pinox67]

There may be a somewhat practical reason to neglect changes to the fundamental.

For sure, the practical reason (perhaps the only one) is that it is difficult to measure.

For one, the energy from the fundamental is distributed into the harmonics/IMD products, lowering its amplitude. Any increase due to the nonlinearity will be offset to some degree by this energy loss due to the harmonics.

It is a bit vague… in the post #10 I’ve already reported what means to consider H1+HD1 or only H1 as fundamental in the calculations.

What's more, a small increase or decrease in the level of the fundamental is much less likely to be audible than the harmonic/IMD products due to masking.

Perhaps a couple of clarifications are needed.

1. HD1 is a harmonic distortion that has the same properties as all the others, only it is hidden in the fundamental. The level of HD2, HD3, etc. does not "fluctuate" for a fixed tone. Thus, even the level of HD1 does not "fluctuate".
2. Here we're not talking about the audibility (there is another thread where I hazard a few hypotheses), but about the correctness of THD as indicator of energy (actually, the RMS value) associated to non-linearities of devices. As you yourself pointed out to me in post #11, it was not born for this goal, with the side effect of losing energy components, sometimes yes, sometimes no.

Not saying it's not interesting to see the effect and how much it contributes, but there are good reasons to ignore it.

So far I have not found any compelling reason.

As you yourself have written in the same post #11, a new indicator would be appropriate for this purpose. For the extent of the deviations, I have already exposed them well at least in the case of circuits memory-less, where it is clear that they are not exactly negligible; for those with memory, it could be more or less, it is to be explored. If there is someone willing...

That said, can you provide a real-life example showing the change in amplitude of the fundamental due to HD1 (not a simulated result)?

With a single tone you can obtain HD1 indirectly, by measuring the module and phase of the other harmonics, as I described in the previous post, at the moment only in the case of circuits memory-less. I know, they are a narrow class, but simulations and measurements are in more than good agreement here.

It could probably be detected directly using a suitable multitone signal, making sure that HD1 is present on some fundamentals and not on others, in a similar way to what happens in fig. 3 of my first post. I need to go deeper.

 

[pkane]

Tube amplifier, as shown in post #17.

Sorry, but what exactly am I seeing that 3D plot? Where is the HD1 part that was added to the fundamental and how was that determined?

 

[pma]

Sorry, but what exactly am I seeing that 3D plot? Where is the HD1 part that was added to the fundamental and how was that determined?

HD1 = fundamental frequency. Its amplitude fluctuates for the reason that the transfer function is not time invariant. This is a fact and is of course more or less pronounced. You can clearly see fluctuations of higher order harmonics, for the exactly same reason. There is no real amplifier with static polynomial transfer function. Such thing exists only in theory and in simulations.

 

[pkane]

HD1 = fundamental frequency. Its amplitude fluctuates for the reason that the transfer function is not time invariant. This is a fact and is of course more or less pronounced. You can clearly see fluctuations of higher order harmonics, for the exactly same reason. There is no real amplifier with static polynomial transfer function. Such thing exists only in theory and in simulations.

That's all true, but doesn't help with the original question about static nonlinearity.

 

[pkane]

For sure, the practical reason (perhaps the only one) is that it is difficult to measure.



It is a bit vague… in the post #10 I’ve already reported what means to consider H1+HD1 or only H1 as fundamental in the calculations.



Perhaps a couple of clarifications are needed.

1. HD1 is a harmonic distortion that has the same properties as all the others, only it is hidden in the fundamental. The level of HD2, HD3, etc. does not "fluctuate" for a fixed tone. Thus, even the level of HD1 does not "fluctuate".
2. Here we're not talking about the audibility (there is another thread where I hazard a few hypotheses), but about the correctness of THD and IMD as indicators of energy (actually, the RMS value) associated to non-linearities of devices. As you yourself pointed out to me in post #11, both were not born for this goal, with the side effect of losing energy components, sometimes yes, sometimes no.

So far I have not found any compelling reason.

As you yourself have written in the same post #11, a new indicator would be appropriate for this purpose. For the extent of the deviations, I have already exposed them well at least in the case of circuits memory-less, where it is clear that they are not exactly negligible; for those with memory, it could be more or less, it is to be explored. If there is someone willing...



With a single tone you can obtain HD1 indirectly, by measuring the module and phase of the other harmonics, as I described in the previous post, at the moment only in the case of circuits memory-less. I know, they are a narrow class, but simulations and measurements are in more than good agreement here.

It could probably be detected directly using a suitable multitone signal, making sure that HD1 is present on some fundamentals and not on others, in a similar way to what happens in fig. 3 of my first post. I need to go deeper.

Far be it for me to defend an old and standard metric that may not be 100% accurate. But then, for consistency in comparisons, perhaps you should still consider a new metric with a new name

 

[Pinox67]

HD1 = fundamental frequency. Its amplitude fluctuates for the reason that the transfer function is not time invariant. This is a fact and is of course more or less pronounced. You can clearly see fluctuations of higher order harmonics, for the exactly same reason. There is no real amplifier with static polynomial transfer function. Such thing exists only in theory and in simulations.

I agree, all amps exhibit memory effects. But there are some that have less than others. I am sure you will know better than me how to verify them. One is that reported in point 2 of post #23: the closer the amplifier is to the characteristics indicated, the more it is free from memory effects and approaches a static transfer function. My electronic technical friends have precisely these characteristics as their goal in their projects, and in some devices they have come very, very close. But these aspects are certainly covered in other threads.

 

[Pinox67]

Far be it for me to defend an old and standard metric that may not be 100% accurate. But then, for consistency in comparisons, perhaps you should still consider a new metric with a new name

The important thing is to understand the purpose of each indicator, what "is inside" and what is not, in order to be able to use it correctly. And the discussion in this thread I think has helped everyone (myself included) to better understand.
For a new indicator, I think there is still a long way to go, and then we have to understand if the market needs it...

 

[Pinox67]

For the rest, IMO the OP premises are incorrect; while some sort of integral transform using a kernel of polynomials can be developed, it would not render any other results than the standard Fourier transform. I believe what the OP considers as "contribution to the fundamental component" is simply a reflection of the obvious effect of energy transfer from the fundamental to the harmonics. Otherwise, I may not understand what's the fuss here. Dear Fourier is good enough, we don't need anything else, unless the OP wants to model a time variant system (like dielectric memory, or thermal behavior). For which no polynomials will ever help.

I'm not sure I understand your comment. What premise or part of the static nonlinear model is incorrect?

As already reported in other posts, this model based on a polynomial kernel only approximates limited classes of amplifiers. But for those with limited (non-linear) memory effects, the agreement between simulation using this model and measurements is very good. The frequency analysis gives us a lot of useful information to understand what here "escapes" from the current THD calculation, while the dual calculation of the THD in the time-domain (see post #11) has no missing parts.

For amplifiers with not negligible memory effects, more sophisticated models are needed, yes. I have already created a simulator based on the Volterra Kernel (here some details). I have to start simulations and comparisons with measurements. The frequency analysis here will be more difficult, since the distortion will depend on the frequency. However, I would expect gradual deviations from the results shown, used as a starting point.

As I said, we need to work on it... suggestions are welcome!

 

[syn08]

I am confused of what you are after here; I don’t even understand what exactly you mean by “static non linear model” in this context, since in the following paragraph you seem to be after a method to analyze time variant systems, which don‘t qualify by definition as “static” (if by “static” you actually mean “stationary”). If so, then see the reference I posted about, it is a rather basic introduction to the frequency dependent Fourier kernels, which is a pretty general, and the most common, approach to this problem. From an engineering perspective, the results are not pretty and, from an audio engineering perspective, definitely moot. As I said above, from all practical purposes, audio electronics is time invariant and of minimum phase; everything else is pretty much in the background noise of the universe.

Speakers and acoustics, you may be on to something, but I wonder if there isn’t a bigger fish to fry in these areas…

 

[Pinox67]

I am confused of what you are after here; I don’t even understand what exactly you mean by “static non linear model” in this context, since in the following paragraph you seem to be after a method to analyze time variant systems, which don‘t qualify by definition as “static” (if by “static” you actually mean “stationary”). If so, then see the reference I posted about, it is a rather basic introduction to the frequency dependent Fourier kernels, which is a pretty general, and the most common, approach to this problem. From an engineering perspective, the results are not pretty and, from an audio engineering perspective, definitely moot. As I said above, from all practical purposes, audio electronics is time invariant and of minimum phase; everything else is pretty much in the background noise of the universe.

Speakers and acoustics, you may be on to something, but I wonder if there isn’t a bigger fish to fry in these areas…

All reported results and the different posts refer to the case of non-linear systems with negligible memory effects, which can be simulated with a static, time-independent, transfer curve. And the discussion that followed is about the representativeness of the THD for the distortions generated by these systems. What I was asking you is mainly about your doubts about the premises that you thought were incorrect.

Having said that, this of THD calculation is a “detail” (not a target) emerged from a larger (ongoing) study aimed at representing larger classes of systems through the Volterra Kernels of which I have made some mention.

 

[syn08]

Ok, correct me if I'm wrong: you are claiming that a time invariant, non linear, two port network, having a 3rd degree polynomial transfer function, excited with a pure sine at the input port, shows not only the 2nd and 3rd harmonics at the output, but the fundamental H1 will also change from what could be a strictly proportional ratio, to the input sine amplitude. From this behavior you conclude that THD, defined as the geometric average of harmonics amplitudes to the fundamental not entirely consistent.

Your claim is correct, and you could intuitively look at such a system as having IMD, and then the H3-H2 component goes to the H1 bin, which obviously always happens. In fact, if you extend the ugly trigonometric algebra, you will mathematically get this H3-H2 intermodulation product too. Ok, so what? This second order intermodulation (adding/subtracting to H1, depending on the phase) products will always be much smaller that the first order intermodulation products (H2, H3) and the linear fundamental H1. Therefore, except for pathological cases where the distortion levels are very high, these 2nd (and 3rd... etc... depending on the non linear transfer function) can usually be safely ignored. It would be a good exercise for you to work up a practical example of an HIFI audio system where these high order intermodulation products would significantly alter the calculated THD. I'm sure characterizing the famous $250K Wavac amplifier using THD is incorrect .

THD is nothing but a definition, and the number provided is just that: a synthetic number. The limitations of this definition is the reason why (for example) DSL signals (where noise and distortions are critical, since they both impact the channel bandwidth and the adjacent channel SNR) are not characterized using THD, but other metrics are used. In fact, I am myself not aware of another domain, other than audio, where the THD metric is consistently used.

 

[Pinox67]

Ok, correct me if I'm wrong: you are claiming that a time invariant, non linear, two port network, having a 3rd degree polynomial transfer function, excited with a pure sine at the input port, shows not only the 2nd and 3rd harmonics at the output, but the fundamental H1 will also change from what could be a strictly proportional ratio, to the input sine amplitude. From this behavior you conclude that THD, defined as the geometric average of harmonics amplitudes to the fundamental not entirely consistent.

Your claim is correct, and you could intuitively look at such a system as having IMD, and then the H3-H2 component goes to the H1 bin, which obviously always happens. In fact, if you extend the ugly trigonometric algebra, you will mathematically get this H3-H2 intermodulation product too. Ok, so what? This second order intermodulation (adding/subtracting to H1, depending on the phase) products will always be much smaller that the first order intermodulation products (H2, H3) and the linear fundamental H1. Therefore, except for pathological cases where the distortion levels are very high, these 2nd (and 3rd... etc... depending on the non linear transfer function) can usually be safely ignored. It would be a good exercise for you to work up a practical example of an HIFI audio system where these high order intermodulation products would significantly alter the calculated THD. I'm sure characterizing the famous $250K Wavac amplifier using THD is incorrect .

THD is nothing but a definition, and the number provided is just that: a synthetic number. The limitations of this definition is the reason why (for example) DSL signals (where noise and distortions are critical, since they both impact the channel bandwidth and the adjacent channel SNR) are not characterized using THD, but other metrics are used. In fact, I am myself not aware of another domain, other than audio, where the THD metric is consistently used.

It is an interesting interpretation
Ok, take a look at the following chart. It is the simulation of the CCIF test with 2 tones at 19KHz and 20KHz with a 1:1 ratio through a system that has only 3rd harmonic distortion at -70dB. Fundamentals are in blue; distortions in orange.

Fig. 5 - CCIF Test Simulation.

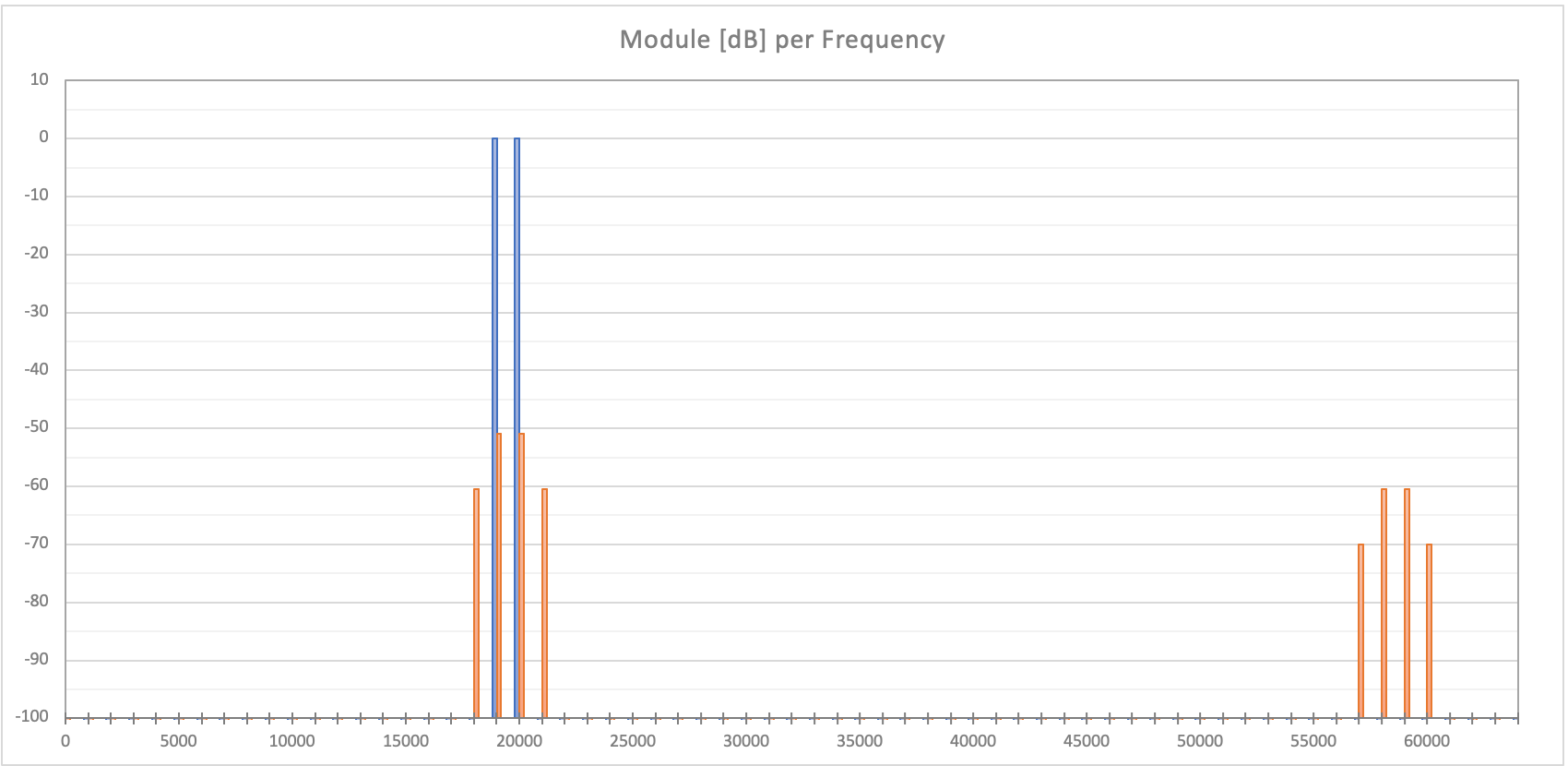
As you can see, HD1s are 10dB higher than all other distortions. If you calculate the TD+N with the classic method, you have an TD+N of -57.2dB (for all bandwidth). Taking into account also the HD1s you have an TD+N -50.0dB (calculated both in the frequency and time domains). It's a 7.2dB discrepancy, not really small...

As I have already said, it is only a question of being aware of what is and what is not in the THD (and TD+N) to avoid using them improperly (with only 2nd harmonic distortion the discrepancy would not have existed). And then, as any good audiophile knows, THD, IMD, TD+N are not directly related to the perceived sound quality of a system, so I wouldn't want to spend too much time on it.

 

[syn08]

Isn't trigonometry a bitch ?

sin(3x)=3 sin(x) - 4 sin^3(x)

So no surprise the intermodulation spectra has a fundamental component. The same question applies... so what? Don't like the THD metric definition, don't use it .

BTW, -70dB 3rd harmonic audio qualifies as "pathologic" in my book... It takes quite some effort to build today a solid state audio amplifier that bad, even open loop (no feedback) designs are significantly better.

 

[Pinox67]

Isn't trigonometry a bitch ?

sin(3x)=3 sin(x) - 4 sin^3(x)

So no surprise the intermodulation spectra has a fundamental component. The same question applies... so what? Don't like the THD metric definition, don't use it .

BTW, -70dB 3rd harmonic audio qualifies as "pathologic" in my book... It takes quite some effort to build today a solid state audio amplifier that bad, even open loop (no feedback) designs are significantly better.

Yes, the formula is that, which you can see in action.
In fact, the values you see shown in tabs 1a and 1b of this post are nothing more than the coefficients of the harmonics sin(jx) the sum of which determine sin^i(x) (the order of distortion), with i = 2, 3, ... 11; Tables 2a and 2b show the related phases.

So what I have already reported is valid: THD (and TD+N) should be taken with a grain of salt, or it is necessary to correct the calculation, including in this not only the NEW distortion harmonics, but ALL, as the definition states. Actually… I don't think the market matters much!

BTW, if you change the level of 3rd harmonic distortion in the example, the discrepancy between the "Classic" and "True" TD+N values remains constant, always -7.2dB.

 

[syn08]

THD and IMD should be taken with a grain of salt, or it is necessary to correct the calculation, including in this not only the NEW distortion harmonics, but ALL, as the definition states.

Only in pathological cases, which is what your examples are all about. When comparing two amplifiers, one decent and one pathological, the difference you reported is totally irrelevant, since the standard THD values are already two orders of magnitude (or more) apart. It's called "engineering", you know; engineers know when to ignore second order effects.