I thought I'd create a thread where suggestions/comments can be made on if Amir were to rank speakers based on measurements, how would he do so.
As of right now, since Amir wants his rating to be based on listening tests and not just opinions, Sean Olive's Predicted Preference rating is likely what will be used for now as it is decently accurate (probability 0.86). I think before suggesting alterations/alternatives, that we should first understand Olive's algorithm; he has filed a patent for it and is available as a searchable PDF (warning: may download instead of view).
Please bear with me.
His algorithm is such:

Here is it as a percentage:

NBD (Narrow Band Deviation): Average Narrow Band Deviation (dB) in each 1/2-octave band from 100 Hz-12 kHz
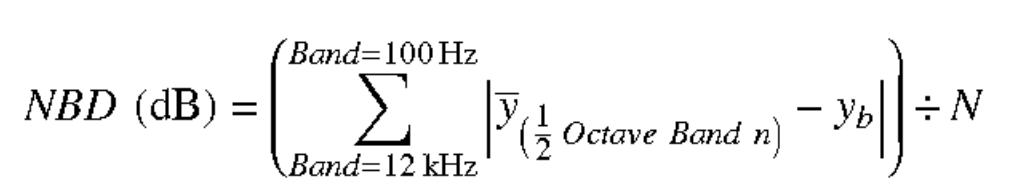
As noted, for rear-firing speakers, making the -6dB point in the Sound Power curve be relative to the average Sound Power SPL may be better than the average Listening Window SPL.
SM_PIR (Smoothness of Predicted In-room Response): Smoothness in SPL based on a linear regression line (at least 1 square error) thru 100Hz-16 kHz.
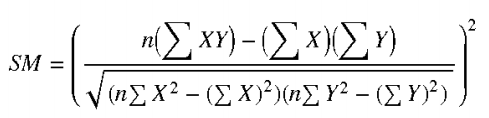
___________________________
Observations & Critiques
That's all I got for now.
Since Dr. Olive has all the data to check, and it is his work being critiqued (possibly improved), I wonder if he would be wiling to run any altered version to see if it obtains a higher correlation.
EDIT: Working on the calculation based off the NHT's text files Amir provided.
As of right now, since Amir wants his rating to be based on listening tests and not just opinions, Sean Olive's Predicted Preference rating is likely what will be used for now as it is decently accurate (probability 0.86). I think before suggesting alterations/alternatives, that we should first understand Olive's algorithm; he has filed a patent for it and is available as a searchable PDF (warning: may download instead of view).
Please bear with me.
His algorithm is such:
Here is it as a percentage:
NBD (Narrow Band Deviation): Average Narrow Band Deviation (dB) in each 1/2-octave band from 100 Hz-12 kHz
NBD_ON: On-axis
NBD_PIR: Predicted In-room Response
- y-bar is the average amplitude value within the 1/2-octave band n
- y-sub(b) is the amplitude value of band b within the 1/2-octave band n
- N is the total number of 1/2-octave bands between 100Hz-12kHz
- NBD can be a good metric for detecting medium and low Q resonances.
LFX (Low Frequency Extension): Log10 of the -6dB point (below 300Hz) in the Sound Power curve, relative to average Listening Window (300Hz-10kHz) SPL.Easy to understand; turning this into a formula:
SM_PIR (Smoothness of Predicted In-room Response): Smoothness in SPL based on a linear regression line (at least 1 square error) thru 100Hz-16 kHz.
It is simply R^2 (correlation squared):
- n is the number of data points used to estimate the regression curve
- X and Y represent the measured versus estimated amplitude values of the regression line.
- A natural log transformation is applied to the measured frequency values so that they are linearly spaced. Smoothness (SM) values can range from 0 to 1, with larger values representing smoother frequency response curves.
___________________________
Observations & Critiques
- THD is not included. Rating THD performance is hard to do as we would have to agree on what is audible. I'll start with a suggestion of a downward slope where audibility thresholds is set to 10% THD @ 20Hz and 0.1% THD @20kHz; this is already considerably lower that what I consider audible, but I reduced it to please others.
- Besides log-scaling, the preference rating does not weight frequencies differently.
- I think NBD_ON may have too much of an effect on the score, we almost never listen solely on the direct axis. I can't alter the algorithm and see if it improves as I don't have Harman's data, but I think it should be changed to a NBD on the Listening Window, or maybe a +/-5° window to not deviate too much.
- Working on the assumption that on-axis is the intended axis, some speakers are designed to have no or little toe-in, so that 15° to 30° off-axis is the reference axis. Same for vertical on-axis.
That's all I got for now.
Since Dr. Olive has all the data to check, and it is his work being critiqued (possibly improved), I wonder if he would be wiling to run any altered version to see if it obtains a higher correlation.
EDIT: Working on the calculation based off the NHT's text files Amir provided.
Last edited:
