Introduction
This post is inspired the thread "Which way is up", started by @René - Acculution.com, and especially by a comment from @BeerBear. In "Which way is up" René shows that when replaying a sine wave, the maximum pressure coincides with the point when the loudspeaker cone is at maximum negative excursion. This is irrefutably true, but on the face of it seems very confusing and counter-intuitive. Apologies for singling out @BeerBear, as he was not alone is asking for a simple explanation of why this happens. There were also a few people asking about the time domain too. I've prepared some animations below.... I hope this adds some clarity and doesn't create yet more confusion but let's see. This is intended to be an accessible post, so I'll try my best to minimise jargon and absolutely no equations. In a couple of places I adjusted the animations to make the physical concepts clearer.
After some thought, I ended up thinking that the most helpful approach would be to look at the situation when the cone starts at rest position and then steps forwards by a set amount (+20mm in this case). Here's how that looks in two different ways. On the left side is a very simple animation of the cone movement, shown as a thick vertical blue line. You can think of this as a cross-section through a flat disc. On the right, the cone position on the vertical axis with time shown on the horizontal axis. I've used a smooth Gaussian step. Labelled on the graph are five phases that the cone goes through in travelling from rest to the eventual 20mm displacement. One key concept that's a prerequisite for understanding this post is that displacement, acceleration and velocity are all ways of describing the motion of a body and they're not independent from one another.
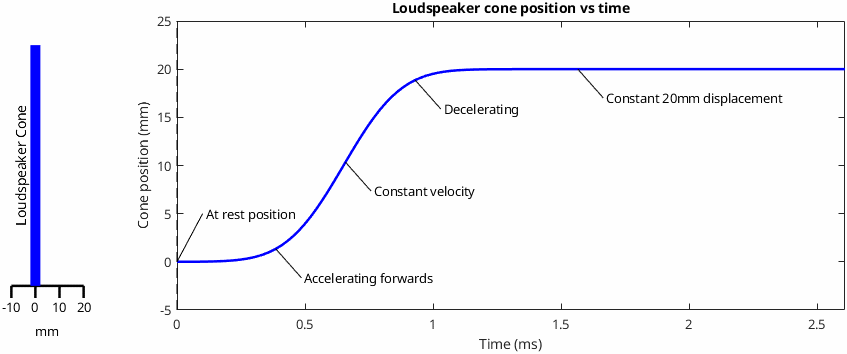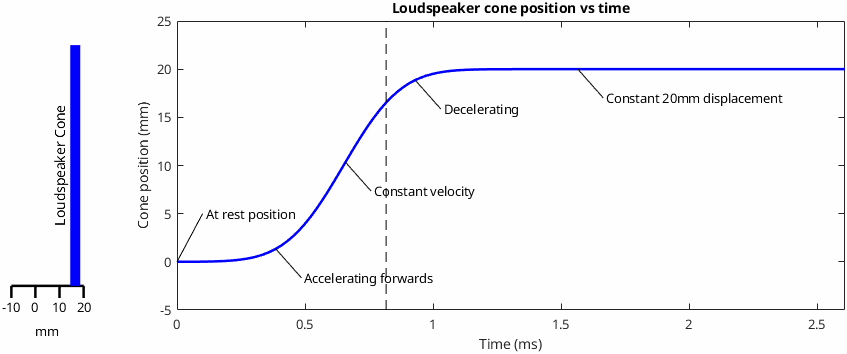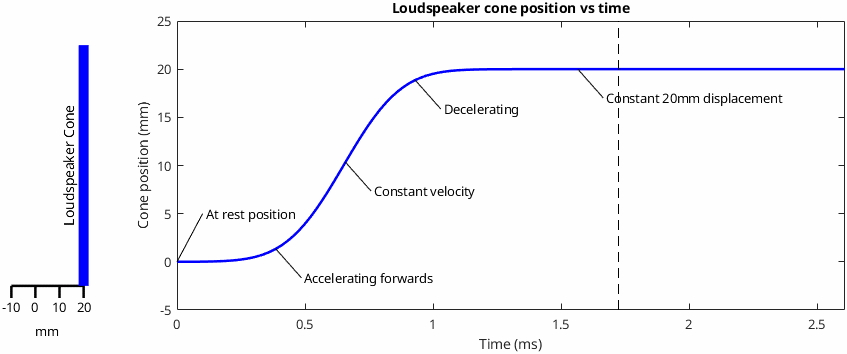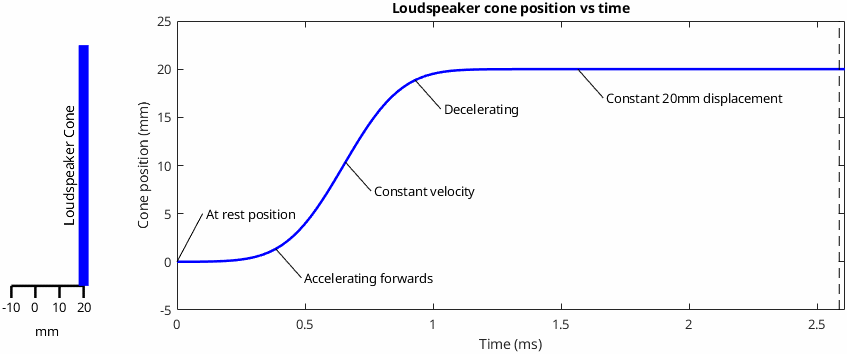
That's the cone movement sorted, so what pressure does it create...? This is the part where it gets slightly complicated, because the resulting acoustical pressure depends on what the cone is driving. We're going to look at three cases, starting with the simplest and most intuitive and ending with the one that gives the surprising result that René showed.
Case 1: The cone drives a enclosed volume of air
If the cone drives a totally sealed volume of air then the acoustical pressure inside the volume increases uniformly with the distance the cone moves*. This makes total sense because no air can escape from the enclosure, and therefore less volume is available when the cone moves forwards. The same amount of air is inside a smaller volume, the "air particles" are forced closer together, and the pressure increases. This behaviour is illustrated below. The little black dots represent air particles and it's easy to see that they're packed more tightly together after the cone has moved forwards.
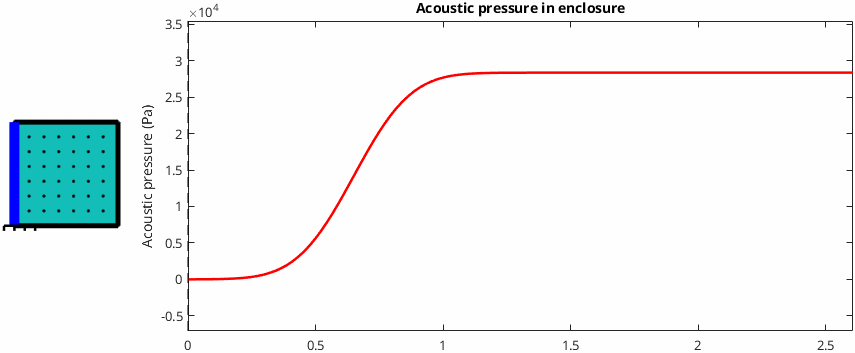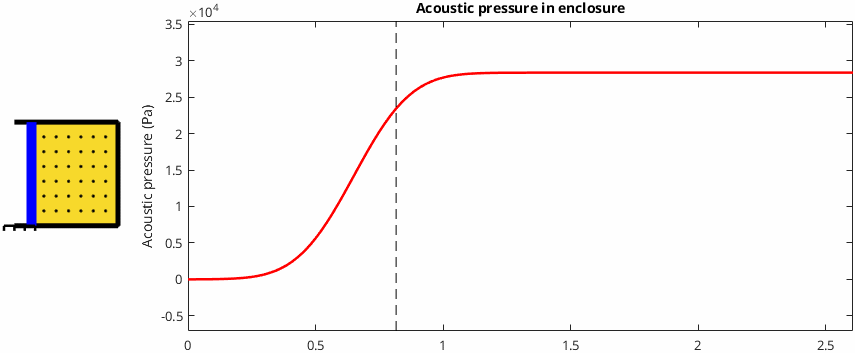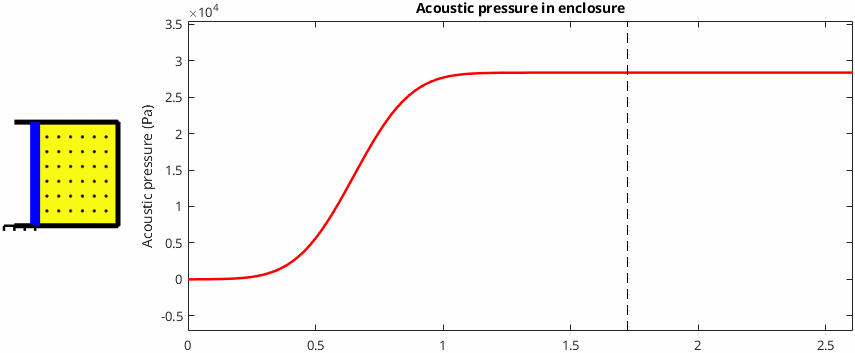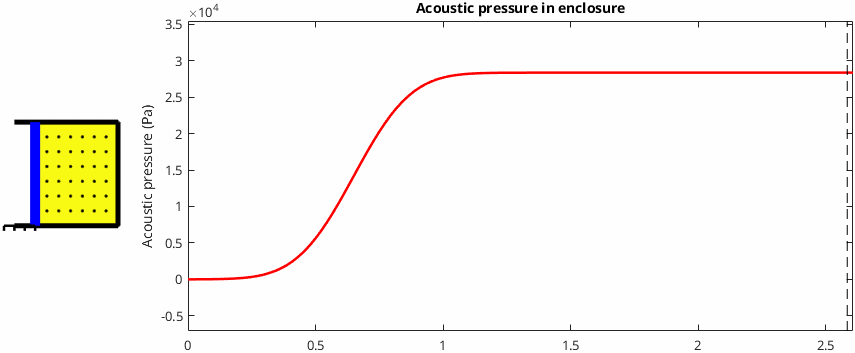
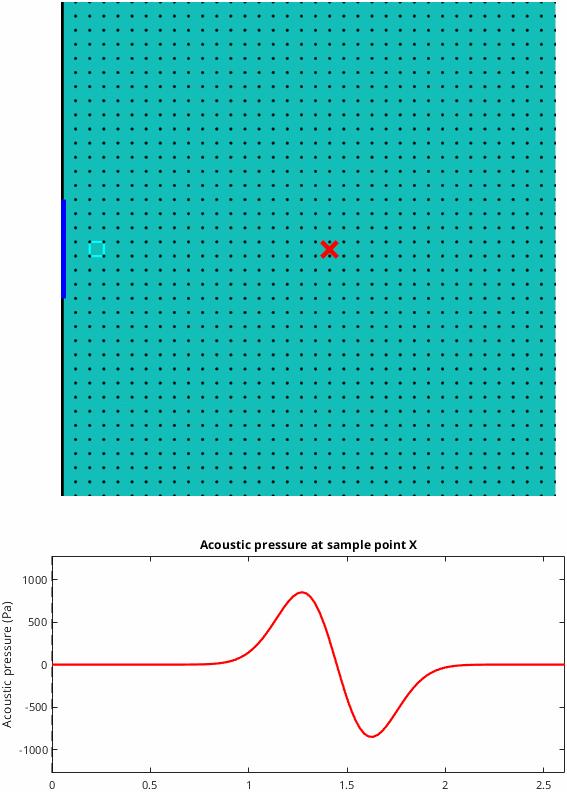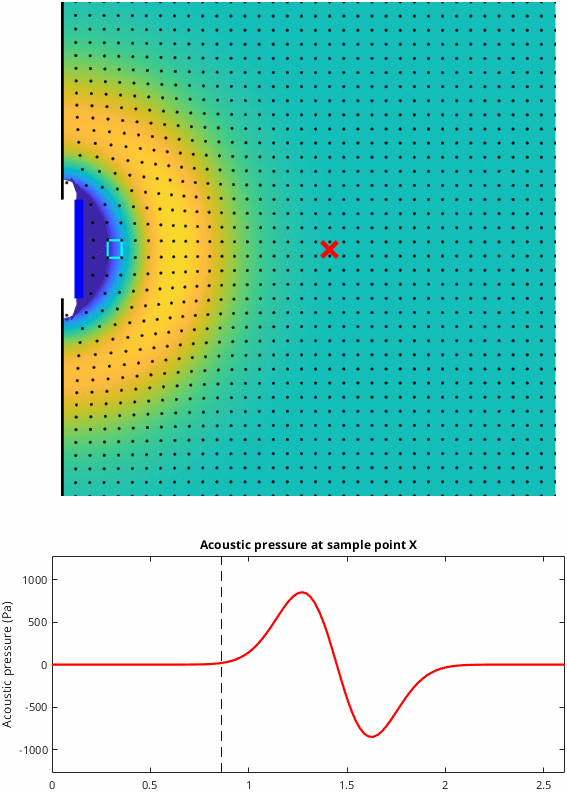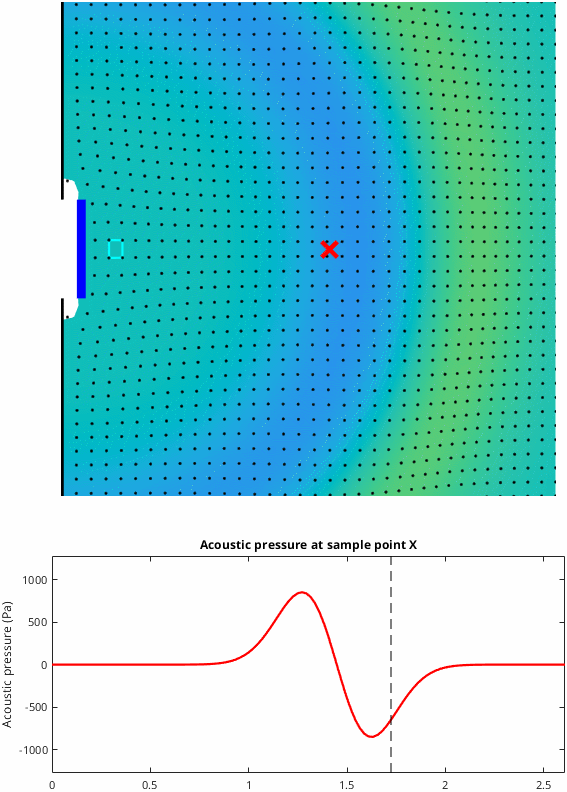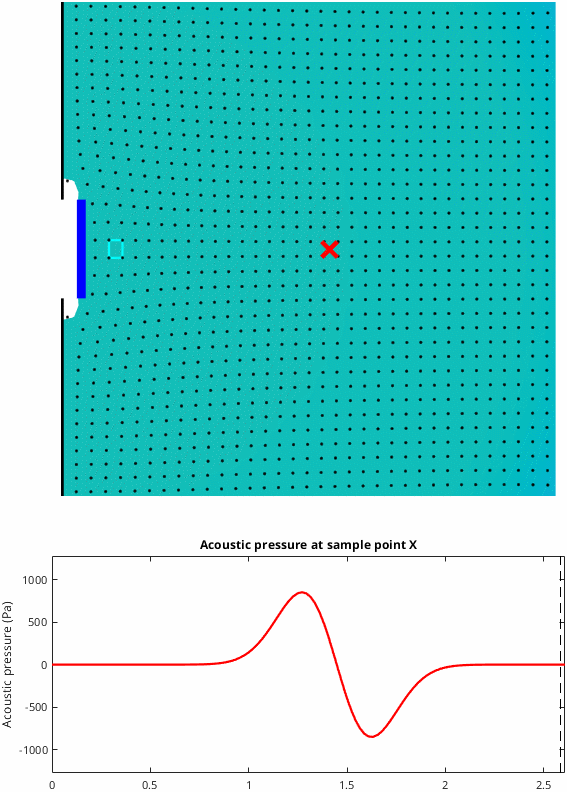
Case 2: The cone drives an extremely long tube of air
If the cone is connected to an extremely long tube then the air is no longer fully enclosed. This means that eventually the entire column of air in the tube is pushed away from the cone and the air returns to the ambient pressure. This means that rather than seeing a step in the pressure, we instead see that the pressure peaks and then reduces again. The maximum peak in the pressure corresponds to the highest velocity of the cone. In-fact the pressure is directly related to the cone velocity in this situation. Note that there is still some restriction of the air; the side walls of the tube along with the fact that the tube is exactly the same size as the cone mean that the air particles only move from left to right and the size and shape of the wave doesn't change, it simply travels along the tube.
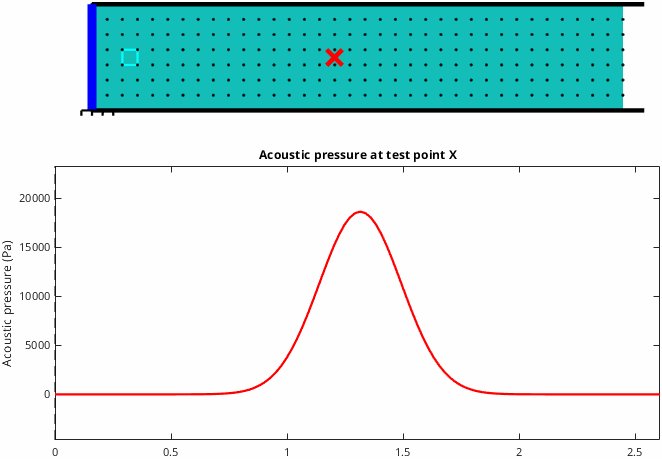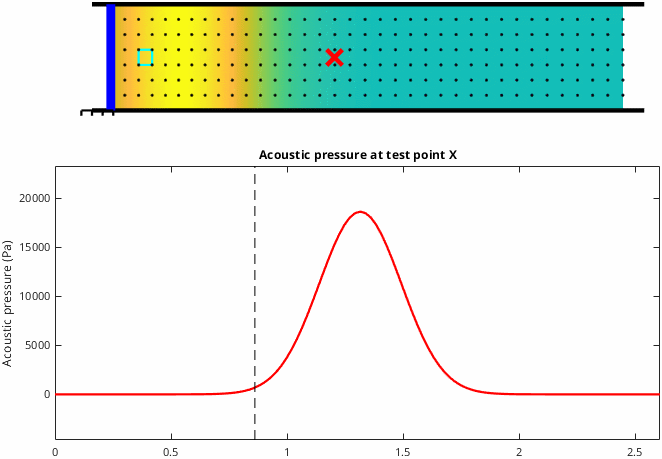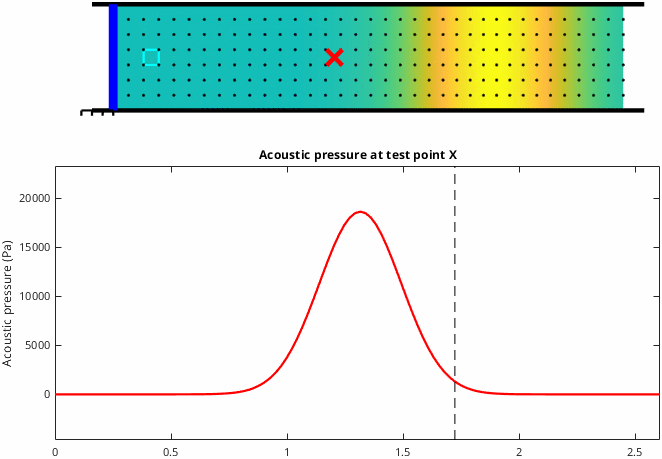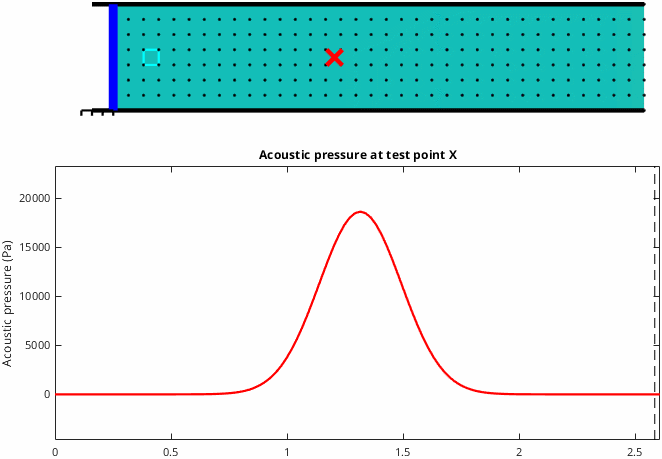
Case 3: The cone is mounted in an infinite baffle
This situation is the closest to what happens with a loudspeaker playing in a room and it's the most difficult case to understand. As the cone pushes forwards, air moves away from the cone in all directions. Initially, during the cone acceleration phase, positive acoustical pressure is generated. However, the critical thing is that the wavefront expands into a larger space and this causes the pressure to reduce quickly as the wave travels away from the cone. In-fact once the cone stops accelerating the pressure returns to zero even though the cone is still in motion, and when the cone decelerates the pressure goes negative. Overall the result is that positive pressure is associated with acceleration of the cone and negative pressure is associated with deceleration of the cone. Note that in the graphic below I've magnified the particle movement to make it visible. Here we see René's result, at maximum cone displacement, negative pressure was generated.
Summary
The outcome of this is that the cone acceleration needs to replicate the recorded audio signal. This is where things get very fortunate because, provided the cone mass dominates the mechanical behaviour (as opposed to the stiffness or damping of the surround/suspension) and the driver motor converts the audio signal directly to a force signal, this will naturally result in cone acceleration that matches the audio signal.**
EDIT: 05/10/2023
To drill down a bit more into the reason why case 2 and case 3 are different I've added two small cyan boxes to the case 2 and case 3 animations above. These boxes represent "volume elements" and we can use them to get a better understanding of the physics of what's going on. I'm hopeful that gives a bit more of an intuitive view of why it's the expansion of the sound-wave that causes the different behaviour in case 2 and case 3.
The pressure inside these volume elements is approximately uniform, so that means it only depends on how the volume element edge lengths are changing as the wave passes. Zooming in on the volume element in case 1 we can see that whole volume element is pushed to the right by the cone movement. The only movement is left to right. The vertical edges of the element are perpendicular to the cone and wave movement and always remain the same length. The horizontal edges are parallel to the cone and wave moment and they are compressed as the wave passes. The compression of the horizontal edges means that the volume element is smaller and hence the pressure is higher during this period.
Case 3 behaves differently in a significant way. The motion of the air particles is not parallel. The air particles "spread out" as they are pushed away from the cone. This means that the vertical edges of the volume element are stretched as the wave passes. It is this stretching motion that leads to negative pressure as soon as the cone starts to decelerate. The final shape of the volume element is no longer square. The final volume of the volume element is the same as the initial volume and hence the initial and final pressure are also the same, but the vertical edges have been stretched and the horizontal edges have been compressed.
*To help keep this simple I've ignored second order effects like standing waves.
**Yes, there's a lot more to it than that, but it's beyond the scope of this post to discuss it here.
This post is inspired the thread "Which way is up", started by @René - Acculution.com, and especially by a comment from @BeerBear. In "Which way is up" René shows that when replaying a sine wave, the maximum pressure coincides with the point when the loudspeaker cone is at maximum negative excursion. This is irrefutably true, but on the face of it seems very confusing and counter-intuitive. Apologies for singling out @BeerBear, as he was not alone is asking for a simple explanation of why this happens. There were also a few people asking about the time domain too. I've prepared some animations below.... I hope this adds some clarity and doesn't create yet more confusion but let's see. This is intended to be an accessible post, so I'll try my best to minimise jargon and absolutely no equations. In a couple of places I adjusted the animations to make the physical concepts clearer.
After some thought, I ended up thinking that the most helpful approach would be to look at the situation when the cone starts at rest position and then steps forwards by a set amount (+20mm in this case). Here's how that looks in two different ways. On the left side is a very simple animation of the cone movement, shown as a thick vertical blue line. You can think of this as a cross-section through a flat disc. On the right, the cone position on the vertical axis with time shown on the horizontal axis. I've used a smooth Gaussian step. Labelled on the graph are five phases that the cone goes through in travelling from rest to the eventual 20mm displacement. One key concept that's a prerequisite for understanding this post is that displacement, acceleration and velocity are all ways of describing the motion of a body and they're not independent from one another.
That's the cone movement sorted, so what pressure does it create...? This is the part where it gets slightly complicated, because the resulting acoustical pressure depends on what the cone is driving. We're going to look at three cases, starting with the simplest and most intuitive and ending with the one that gives the surprising result that René showed.
Case 1: The cone drives a enclosed volume of air
If the cone drives a totally sealed volume of air then the acoustical pressure inside the volume increases uniformly with the distance the cone moves*. This makes total sense because no air can escape from the enclosure, and therefore less volume is available when the cone moves forwards. The same amount of air is inside a smaller volume, the "air particles" are forced closer together, and the pressure increases. This behaviour is illustrated below. The little black dots represent air particles and it's easy to see that they're packed more tightly together after the cone has moved forwards.
Case 2: The cone drives an extremely long tube of air
If the cone is connected to an extremely long tube then the air is no longer fully enclosed. This means that eventually the entire column of air in the tube is pushed away from the cone and the air returns to the ambient pressure. This means that rather than seeing a step in the pressure, we instead see that the pressure peaks and then reduces again. The maximum peak in the pressure corresponds to the highest velocity of the cone. In-fact the pressure is directly related to the cone velocity in this situation. Note that there is still some restriction of the air; the side walls of the tube along with the fact that the tube is exactly the same size as the cone mean that the air particles only move from left to right and the size and shape of the wave doesn't change, it simply travels along the tube.
Case 3: The cone is mounted in an infinite baffle
This situation is the closest to what happens with a loudspeaker playing in a room and it's the most difficult case to understand. As the cone pushes forwards, air moves away from the cone in all directions. Initially, during the cone acceleration phase, positive acoustical pressure is generated. However, the critical thing is that the wavefront expands into a larger space and this causes the pressure to reduce quickly as the wave travels away from the cone. In-fact once the cone stops accelerating the pressure returns to zero even though the cone is still in motion, and when the cone decelerates the pressure goes negative. Overall the result is that positive pressure is associated with acceleration of the cone and negative pressure is associated with deceleration of the cone. Note that in the graphic below I've magnified the particle movement to make it visible. Here we see René's result, at maximum cone displacement, negative pressure was generated.
Summary
- In all cases the initial acoustical pressure has positive polarity corresponding to forward movement of the cone from rest position.
- When a speaker drives a sealed volume, the acoustic pressure in the volume is proportional to the cone displacement
- When a speaker drives a long tube, the acoustic pressure in the tube is proportional to the cone velocity.
- When a speaker drives an open space, the acoustic pressure in the space is proportional to the cone acceleration.
- Only the first case, the enclosure, can result in a static change in the acoustic pressure.
The outcome of this is that the cone acceleration needs to replicate the recorded audio signal. This is where things get very fortunate because, provided the cone mass dominates the mechanical behaviour (as opposed to the stiffness or damping of the surround/suspension) and the driver motor converts the audio signal directly to a force signal, this will naturally result in cone acceleration that matches the audio signal.**
EDIT: 05/10/2023
To drill down a bit more into the reason why case 2 and case 3 are different I've added two small cyan boxes to the case 2 and case 3 animations above. These boxes represent "volume elements" and we can use them to get a better understanding of the physics of what's going on. I'm hopeful that gives a bit more of an intuitive view of why it's the expansion of the sound-wave that causes the different behaviour in case 2 and case 3.
The pressure inside these volume elements is approximately uniform, so that means it only depends on how the volume element edge lengths are changing as the wave passes. Zooming in on the volume element in case 1 we can see that whole volume element is pushed to the right by the cone movement. The only movement is left to right. The vertical edges of the element are perpendicular to the cone and wave movement and always remain the same length. The horizontal edges are parallel to the cone and wave moment and they are compressed as the wave passes. The compression of the horizontal edges means that the volume element is smaller and hence the pressure is higher during this period.
Case 3 behaves differently in a significant way. The motion of the air particles is not parallel. The air particles "spread out" as they are pushed away from the cone. This means that the vertical edges of the volume element are stretched as the wave passes. It is this stretching motion that leads to negative pressure as soon as the cone starts to decelerate. The final shape of the volume element is no longer square. The final volume of the volume element is the same as the initial volume and hence the initial and final pressure are also the same, but the vertical edges have been stretched and the horizontal edges have been compressed.
*To help keep this simple I've ignored second order effects like standing waves.
**Yes, there's a lot more to it than that, but it's beyond the scope of this post to discuss it here.
Last edited:
