This opening post is to demonstrate how different loudspeaker low frequency directvity patterns couple to our room modes. If you are unfamiliar with what room modes are, please refer to @DonH56's excellent thread for an in-depth introduction.

 www.audiosciencereview.com
www.audiosciencereview.com
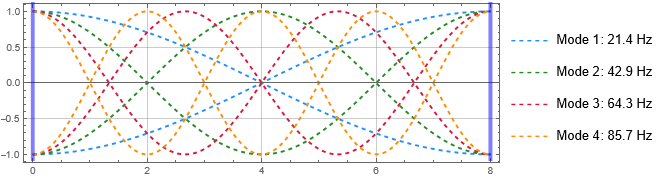
In this post we'll look at a simple case of a longitudinal mode. This example ficticious "1D room" is 8 m long. The first (lowest frequency) room mode is when the room length matches 1/2 of the wavelength, λ. The wavelength of a single tone soundwave is the speed of sound (c = 343 m/s at 20 degC) divided by the frequency (f), i.e. λ = c / f. Therefore, for this room, the first mode is: f_mode_1 = c / (2*room_length) = 21.4 Hz. Higher modes occur at integer mulitple of the lowest mode frequency. In this exercise, we will concentrate on the third mode (64.3 Hz).
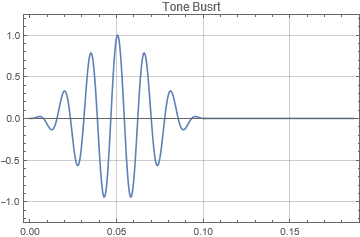
The test signal is a 6.5 cycle raised cosine windowed tone burst. The driver is represented with an up-and-down oscillating dot.
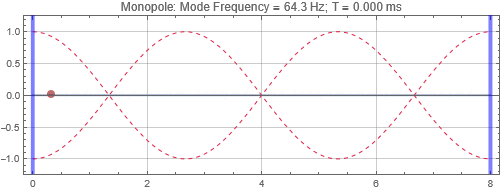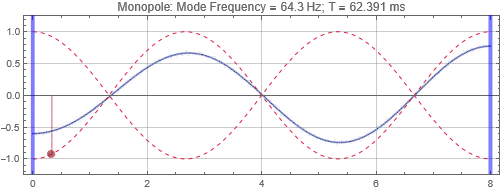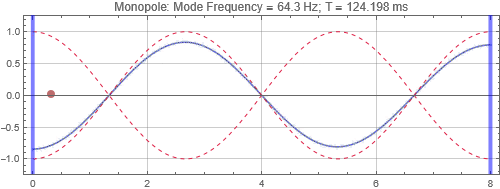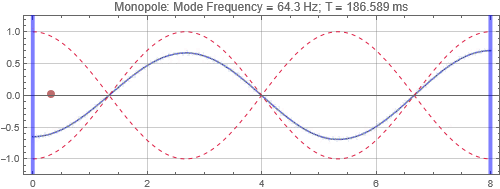
Monopole
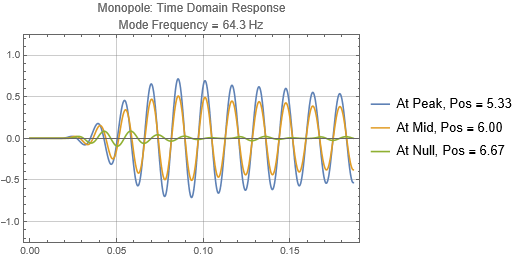
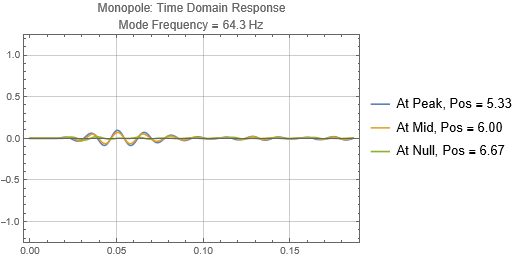
We first start with the most common type by far — the monopole, which radiates omnidirectionally at low frequencies — when wavelengths are much larger than the size of the speakers. We'll look at 3 speaker placement positions, near the left wall, at a null, and at a peak 1/3 of the way into the room. We'll also look at the sound pressures received at 3 listening positions, first one at 5.33 m from the left wall, corresponding to a room mode peak, second is at 6 m and is half way between the peak and the null, and third is at the 6.67 m null.
Monopole located near the left wall
Monopole located at the first null from the left wall
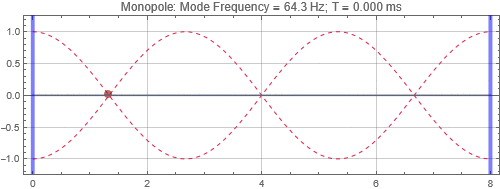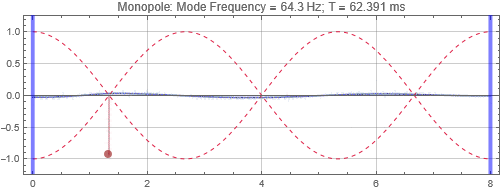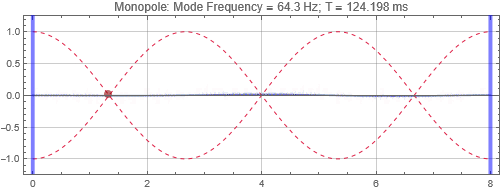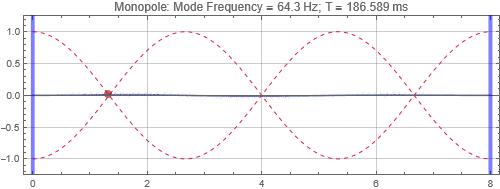
Monopole located at the peak at 1/3 distance into the room
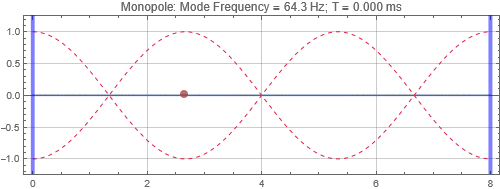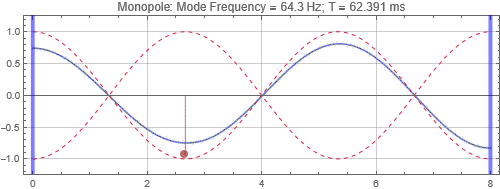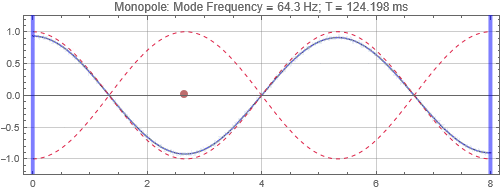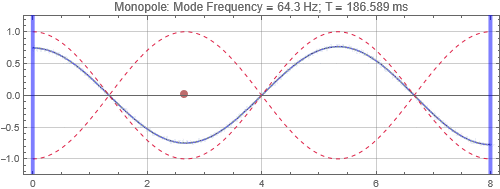
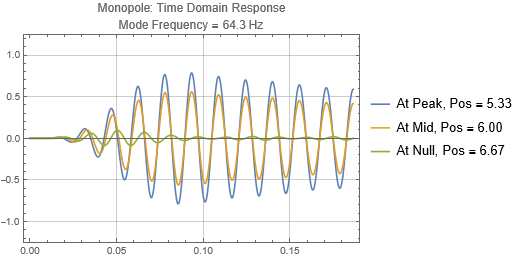
There is no surprise here. When the speaker is located near a peak, it couples strongly to the mode, and the tone reverberates for a long time. Opposite when the speaker is at a null. Notice that the sound as received at the listening position depends on both the speaker position and listener position. If the listener is at a null (the green traces in plots on the right), it doesn't matter if the speaker is located at a peak, the listener will get minimal response for that mode frequency.
Dipole
A dipole can be seen as two monopoles of opposite polarities, separated by a small distance (0.25 m in this case).
Dipole located near the left wall
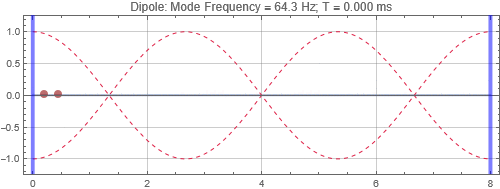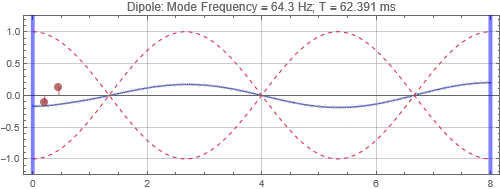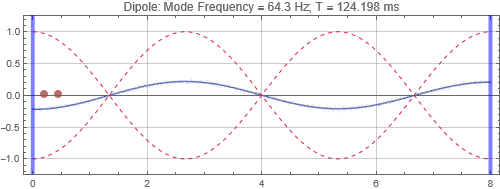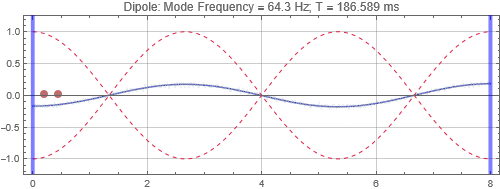
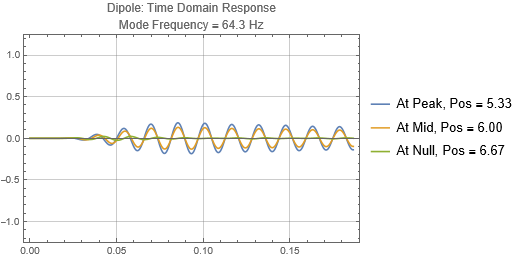
Dipole located at the first null from the left wall
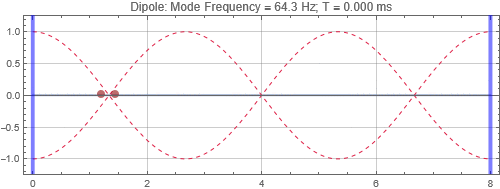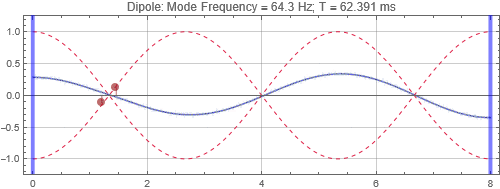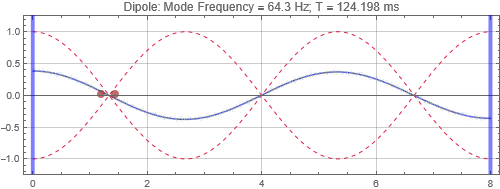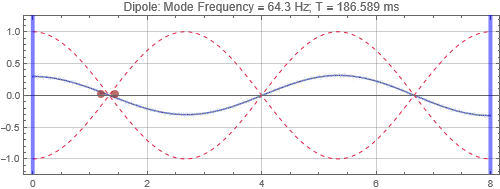
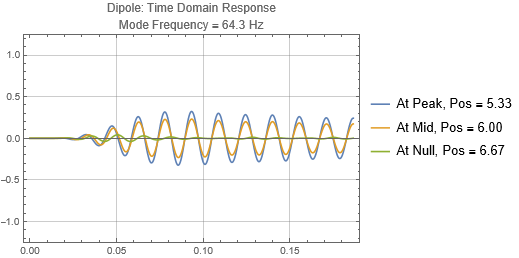
Dipole located at the peak at 1/3 distance into the room
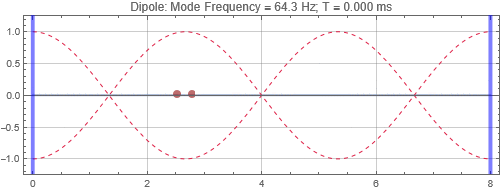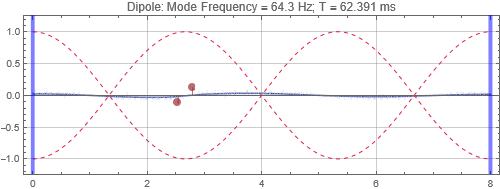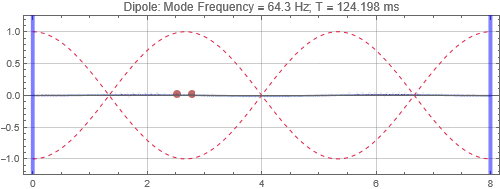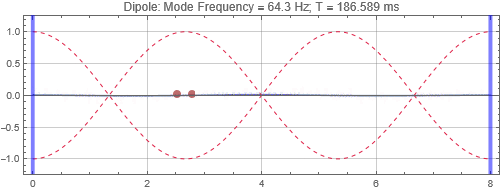
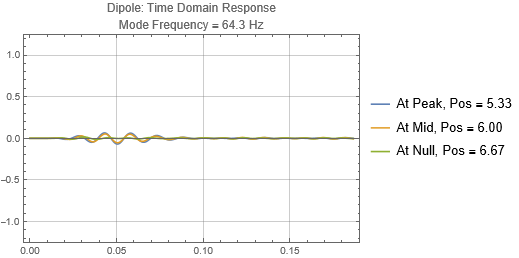
Dipoles couple to rooms in the opposite way as monopoles. It couples poorly when it is at the room mode peak, and couples strongly at the null. Since you will usually find many room mode peaks near room corners, dipoles would be best placed some distance away. Note that a dipole is directional — its orientation matters. You'll only get the response shown here when the dipole orientation aligns to the room mode direction. Also note that a dipole is a lot less efficient as a bass radiator than a monopole because of the significant cancellations by the opposing sound radiators. In this simulation, two "drivers" each of the same power as the monopole are used, and the resulting responses at the listening positions are less than that of a monopole with half the total output power. (See below)
[Edit - Corrections]
When I wrote the original post, I forgot that you don't need 2 drivers to realize a dipole or cardioid radiator (unlike in my simulations which used point sources). The back waves from the driver diaphragm will serve nicely as the opposite polarity source. Open baffle dipoles are just such an implementation. Cardioids can also be realized by acoustically restricting the back waves to give the delay (passive cardioids). It is still true that dipoles and cardioids are inefficient acoustic radiators compared to monopoles, just not nearly as much as it was suggested in my wordings in the original post.
Cardioid
A cardioid is modeled similarly to a dipole (two monopoles of opposite polarity), but with the rear radiator delayed by the time it takes for the sound waves of the front radiator to travel to the back. The result is that, for the soundwaves radiating towards the back, those waves from the rear cancels those from the front. This give the cardioid its characteristic radiation pattern that it has a much reduced sound output towards the back, which can be seen in the animations.
Cardioid located near the left wall
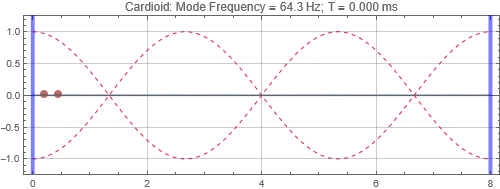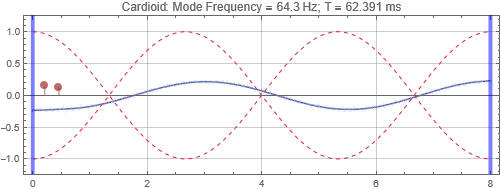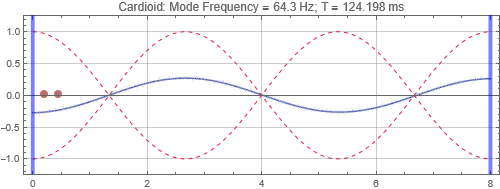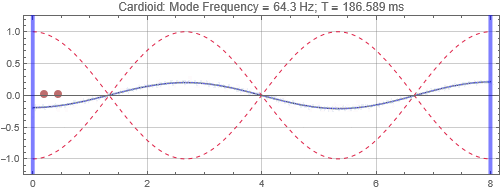
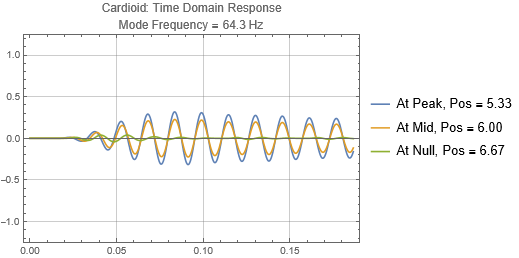
Cardioid located at the first null from the left wall
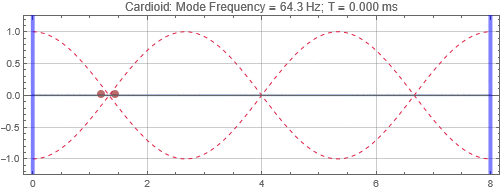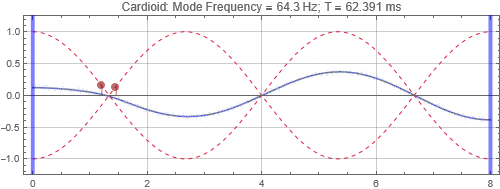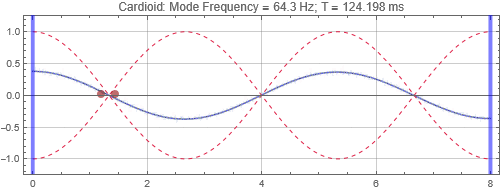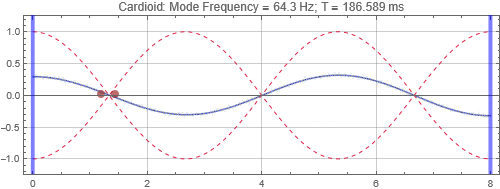
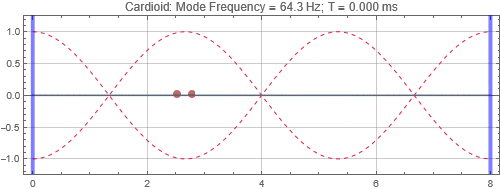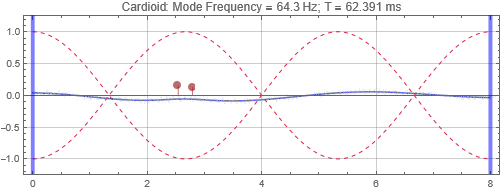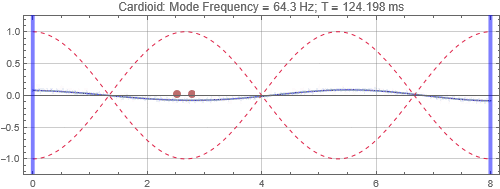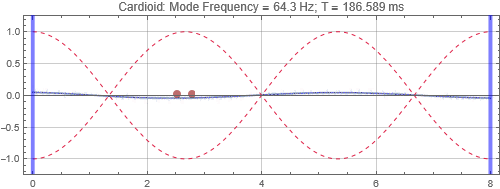
Cardioid located at the peak at 1/3 distance into the room (notice that initially there is no sound radiated to the left due to the cardioid directivity pattern)
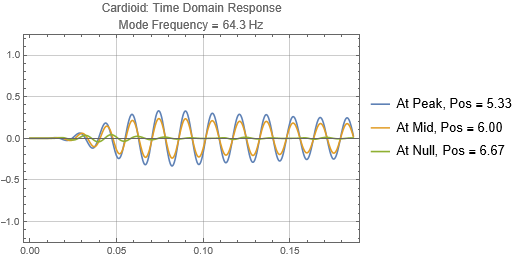
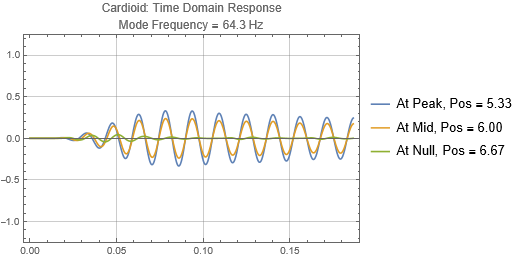
The responses received at the listening positions are largely independent on whether the cardioid speaker is located at a peak or null or in between. Just like the dipole, cardioid is directional, and its effectiveness is dependent on whether it is aligned to the room mode direction. Again, cardioid has low efficiency.
Cardioids have the benefit of radiating most of its energy towards the front hemisphere, thereby exciting the lateral room modes less. The cardioid radiation pattern is difficult to maintain at the low bass frequencies, as the long wavelengths will require larger separation distance between the drivers. The mighty Genelec W371A transitions to omni at ~50 Hz. The a little less mighty Dutch & Dutch 8C transitions at ~100 Hz.
Summary (TL/DR)
Monopoles and dipoles couple to the room in opposite ways, so a good location for a monopole is probably a bad location for a dipole, and vice versa.
To get the desired effects from dipoles and cardioids, they need to be oriented to align with the room modes.
Cardioids are significantly less affected by room modes.
Cardioids and dipoles are inefficient sound radiators compared to monopoles.

Room Modes
Room interactions are often discussed as one of the primary reasons similar (or even dissimilar) systems sound different. If you read the “Reflections and DACs” thread you saw how reflections and standing waves can interact along a transmission line. As it happens, sound waves in a room also...
 www.audiosciencereview.com
www.audiosciencereview.com
In this post we'll look at a simple case of a longitudinal mode. This example ficticious "1D room" is 8 m long. The first (lowest frequency) room mode is when the room length matches 1/2 of the wavelength, λ. The wavelength of a single tone soundwave is the speed of sound (c = 343 m/s at 20 degC) divided by the frequency (f), i.e. λ = c / f. Therefore, for this room, the first mode is: f_mode_1 = c / (2*room_length) = 21.4 Hz. Higher modes occur at integer mulitple of the lowest mode frequency. In this exercise, we will concentrate on the third mode (64.3 Hz).
The test signal is a 6.5 cycle raised cosine windowed tone burst. The driver is represented with an up-and-down oscillating dot.
Monopole
We first start with the most common type by far — the monopole, which radiates omnidirectionally at low frequencies — when wavelengths are much larger than the size of the speakers. We'll look at 3 speaker placement positions, near the left wall, at a null, and at a peak 1/3 of the way into the room. We'll also look at the sound pressures received at 3 listening positions, first one at 5.33 m from the left wall, corresponding to a room mode peak, second is at 6 m and is half way between the peak and the null, and third is at the 6.67 m null.
Monopole located near the left wall
Monopole located at the first null from the left wall
Monopole located at the peak at 1/3 distance into the room
There is no surprise here. When the speaker is located near a peak, it couples strongly to the mode, and the tone reverberates for a long time. Opposite when the speaker is at a null. Notice that the sound as received at the listening position depends on both the speaker position and listener position. If the listener is at a null (the green traces in plots on the right), it doesn't matter if the speaker is located at a peak, the listener will get minimal response for that mode frequency.
Dipole
A dipole can be seen as two monopoles of opposite polarities, separated by a small distance (0.25 m in this case).
Dipole located near the left wall
Dipole located at the first null from the left wall
Dipole located at the peak at 1/3 distance into the room
Dipoles couple to rooms in the opposite way as monopoles. It couples poorly when it is at the room mode peak, and couples strongly at the null. Since you will usually find many room mode peaks near room corners, dipoles would be best placed some distance away. Note that a dipole is directional — its orientation matters. You'll only get the response shown here when the dipole orientation aligns to the room mode direction. Also note that a dipole is a lot less efficient as a bass radiator than a monopole because of the significant cancellations by the opposing sound radiators.
[Edit - Corrections]
When I wrote the original post, I forgot that you don't need 2 drivers to realize a dipole or cardioid radiator (unlike in my simulations which used point sources). The back waves from the driver diaphragm will serve nicely as the opposite polarity source. Open baffle dipoles are just such an implementation. Cardioids can also be realized by acoustically restricting the back waves to give the delay (passive cardioids). It is still true that dipoles and cardioids are inefficient acoustic radiators compared to monopoles, just not nearly as much as it was suggested in my wordings in the original post.
Cardioid
A cardioid is modeled similarly to a dipole (two monopoles of opposite polarity), but with the rear radiator delayed by the time it takes for the sound waves of the front radiator to travel to the back. The result is that, for the soundwaves radiating towards the back, those waves from the rear cancels those from the front. This give the cardioid its characteristic radiation pattern that it has a much reduced sound output towards the back, which can be seen in the animations.
Cardioid located near the left wall
Cardioid located at the first null from the left wall
Cardioid located at the peak at 1/3 distance into the room (notice that initially there is no sound radiated to the left due to the cardioid directivity pattern)
The responses received at the listening positions are largely independent on whether the cardioid speaker is located at a peak or null or in between. Just like the dipole, cardioid is directional, and its effectiveness is dependent on whether it is aligned to the room mode direction. Again, cardioid has low efficiency.
Cardioids have the benefit of radiating most of its energy towards the front hemisphere, thereby exciting the lateral room modes less. The cardioid radiation pattern is difficult to maintain at the low bass frequencies, as the long wavelengths will require larger separation distance between the drivers. The mighty Genelec W371A transitions to omni at ~50 Hz. The a little less mighty Dutch & Dutch 8C transitions at ~100 Hz.
Summary (TL/DR)
Monopoles and dipoles couple to the room in opposite ways, so a good location for a monopole is probably a bad location for a dipole, and vice versa.
To get the desired effects from dipoles and cardioids, they need to be oriented to align with the room modes.
Cardioids are significantly less affected by room modes.
Cardioids and dipoles are inefficient sound radiators compared to monopoles.
Last edited:

