-
WANTED: Happy members who like to discuss audio and other topics related to our interest. Desire to learn and share knowledge of science required. There are many reviews of audio hardware and expert members to help answer your questions. Click here to have your audio equipment measured for free!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How does a loudspeaker cone generate acoustical pressure?
- Thread starter jackocleebrown
- Start date
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,309
For a spring-damper-mass system the external forces will distribute differently depending on the frequency. At very low frequencies (pseudo-static) the force goes into compressing the spring, but the acceleration can be as low as you want it, and so can the velocity, so the other two forces (mass, damper) can be ignored. Around the resonance frequency it is all about the damping, as the spring and the mass can keep each other going, exchanging kinetic and potential energy. Without any damping, they could do so forever. But at higher frequencies above the resonance frequency, the force of the mass dominates, as it is now a forceful action to rapidly change the direction of the mass. A traditional loudspeaker driver is pretty much a s-d-m system with a resonance frequency below its operating frequency range, and hence the 'mass dominates' in the audio range. Not all driver work via this principle.
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,309
Hmmm, I am not sure I would try and make an analogy there. On a hard wall the normal velocity is decidedly zero over a full period, so I am not sure there is anything to had by comparing that to what happens at some instant in another situation. It the former case the sound field is forced from somewhere else, in the later the driver is forcing the field.@jackocleebrown @René - Acculution.com
Similar thing happens in acoustics, where air velocity decreases as it approaches a wall but pressure increases, max pressure/zero velocity being on the wall.
Is there some analogy between that and a driver approaching x-max? Could you please comment?
Curvature
Major Contributor
- Joined
- May 20, 2022
- Messages
- 1,116
- Likes
- 1,410
Thanks. It was a passing thought.Hmmm, I am not sure I would try and make an analogy there. On a hard wall the normal velocity is decidedly zero over a full period, so I am not sure there is anything to had by comparing that to what happens at some instant in another situation. It the former case the sound field is forced from somewhere else, in the later the driver is forcing the field.
- Thread Starter
- #25
Hi Jorge,(My markings in boldface)
Thanks @jackocleebrown for your great educational post. Just some comments to try to complete the exposition (if you find these too basic or obvious, just ignore this post):
1.
Cone and suspension form an elastic system, and all elastic systems have mass, stiffness and dumping, with all three effects contributing in some amount to the "force" in Newton law during the cone movement.
With this in mind, could you explain more precisely what is intended by the highlighted "mass dominates..."?
I know that you wanted to keep equations to a minimum, but given that you already mentioned the Newton law in the "F=Ma" form, perhaps it would be pedagogically useful to include here also the "Ku" and "Cv" terms. Standard texts on vibrations present this as:
F_ext = Ma+Cv+Ku
where a, v, u are respectively acceleration, velocity and displacement and, M, C, K are mass, damping and stiffness of the structure or medium. I like to interpret this form of the Newton law as "Inertial forces are the difference between external forces and internal forces", where internal forces are the forces due to the stiffness and damping of the medium.
Again, in this context, how should one interpret the "mass dominates..." quote?
2.
Regarding the three great looking animations in your original post, we see that in the first one, compression of the enclosed air is a static process, while in the two subsequent ones (long tube and emission to a room) there is wave propagation. So, what determines if wave propagation will or won't occur in a certain medium? The concept of "wavelength" and wavelength-to-enclosure-size "ratio" play a role here. If the box size is less than the wavelength, then simply there is not enough space to be travelled by a wave, and the compression looks as a static process. On the contrary, wave propagation may eventually occur if the box size is larger than the wavelength (and a room is just a larger box), as there is travel distance available for a wave and also, because the very same Newton law imposes, when all terms are considered, that force applied at a certain point in space takes some time and distance to produce an effect at a remote location.
3.
Electrostats and Manger-style drivers have been mentioned in the comments. In these, and also in cones, wave propagation may occur in the same manner as described in point 2., except that in 2. the medium is enclosed air and here, it is the elastic solid material of the membrane or cone. Elastic properties and density of these materials determine their wave propagation velocity, while this velocity together with frequency of an excitation determines wavelength. Finally relationship between wavelength and medium size (cone or membrane size) determine if wave propagation will occur inside the membrane or cone. If this happens, it is informally known as membrane or cone ringing. If not, it is said, roughly, that the behavior of the membrane or cone is pistonic. Most manufacturers try to avoid ringing, but some try to use it in some way (remember reading something to this effect in some white paper or web info from Mark Audio drivers, but not truly sure, maybe it was Jordan?). Is ringing used or avoided in Manger or electrostats drivers?
Regards and thanks again for your post,
Jorge
I saw that René replied to you but only just realised there were some other questions you posed too.
1. You're right, I'm simplifying things to an extreme extent by just focusing on the mass. You're quite right to flag the stiffness and damping of the elastic system. I also ignored motor effects like back-emf and cabinet loading effects too. The thing I was trying to highlight is that the fact that acceleration is proportional to radiated pressure is wonderfully convenient because in the pass-band of the speaker (e.g. > 2*fc) it's possible to have a very wide region where the mechanical impedance looks like a mass and the speaker can have a flat response.
2. In all cases there should be wave-behaviour but I ignored it in case 1 just for simplicity. Had I included it the animation would only be quite subtly different, with an added rapid ripple bounding back and forwards between the cone and the right-hand wall of the enclosure. I think that you're right, however, to say that "simply there is not enough space to be travelled by a wave, and the compression looks as a static process". There are two ways to solve the wave equation in enclosed spaces, one of them is based on superposition of travelling acoustic waves and you could use this approach to solve case 1 and case 2 with the same equations. These equations would reveal that case 1 has travelling waves in both directions (cone to rear-enclosure wall and rear-enclosure wall to cone) and case 2 only has travelling waves away from the cone. In this sense there's no distinction between the two cases and wave-propagation is present in both. The other way to solve the wave equation for case 1 is to use a modal approach, and this would tell you that the first standing wave is related to the longest dimension of the enclosure, and from this you could conclude that, if this standing wave is many octaves above the spectrum of the test signal, you can say the compression looks like a static process.
3. I've often seen cone/driver membrane behaviour described in terms of a wave propagating from the voice coil to the edge of the cone. This normally is followed by the concept of having just the right terminating impedance at the cone edge to absorb this wave. It's a nice concept but I don't thing that many (any?) drivers can possibly really achieve this ideal.... perhaps the Manger does because it has a very simple structure. Perhaps electrostatics too. But certainly with a cone driver the material properties of the cone and surround are so totally different from one another, and the way that the cone geometry stiffens the structure is not uniform (much lower at the outside edge of the diaphragm), there will be a combination of compression and shear waves.... I just can't see if happening in reality. A modal description is probably a better way to look at things, and this will reveal a low frequency mode that's the equivalent to the simple mass, spring, damper model of the driver (the pistonic behaviour) and then higher frequency modes (the breakup). The breakup modes are the ones that can lead to the ringing you talk about. Normally the designer will try and either not excite these modes (for example, by choice of coil position), damp these modes with lossy materials, or possibly there might be some modes that don't result in much sound radiation. Yes, there are designs that try and use the ringing of these modes. Most notably the BMR driver concept invented by NXT, the NXT DML loudspeaker, and I guess you could also throw in the densely modal cone drivers into the mix too: typically woven Kevlar. In all cases the reward for using these modes is higher output and wider directivity at high frequencies. The penalty is potentially in the evenness of the frequency and directional response.
Kind regards,
Jack.
Jerk.This equation is valid if force varies with time
Only here.
Thanks Jack and also René!Hi Jorge,
I saw that René replied to you but only just realised there were some other questions you posed too.
1. You're right, I'm simplifying things to an extreme extent by just focusing on the mass. You're quite right to flag the stiffness and damping of the elastic system. I also ignored motor effects like back-emf and cabinet loading effects too. The thing I was trying to highlight is that the fact that acceleration is proportional to radiated pressure is wonderfully convenient because in the pass-band of the speaker (e.g. > 2*fc) it's possible to have a very wide region where the mechanical impedance looks like a mass and the speaker can have a flat response.
2. In all cases there should be wave-behaviour but I ignored it in case 1 just for simplicity. Had I included it the animation would only be quite subtly different, with an added rapid ripple bounding back and forwards between the cone and the right-hand wall of the enclosure. I think that you're right, however, to say that "simply there is not enough space to be travelled by a wave, and the compression looks as a static process". There are two ways to solve the wave equation in enclosed spaces, one of them is based on superposition of travelling acoustic waves and you could use this approach to solve case 1 and case 2 with the same equations. These equations would reveal that case 1 has travelling waves in both directions (cone to rear-enclosure wall and rear-enclosure wall to cone) and case 2 only has travelling waves away from the cone. In this sense there's no distinction between the two cases and wave-propagation is present in both. The other way to solve the wave equation for case 1 is to use a modal approach, and this would tell you that the first standing wave is related to the longest dimension of the enclosure, and from this you could conclude that, if this standing wave is many octaves above the spectrum of the test signal, you can say the compression looks like a static process.
3. I've often seen cone/driver membrane behaviour described in terms of a wave propagating from the voice coil to the edge of the cone. This normally is followed by the concept of having just the right terminating impedance at the cone edge to absorb this wave. It's a nice concept but I don't thing that many (any?) drivers can possibly really achieve this ideal.... perhaps the Manger does because it has a very simple structure. Perhaps electrostatics too. But certainly with a cone driver the material properties of the cone and surround are so totally different from one another, and the way that the cone geometry stiffens the structure is not uniform (much lower at the outside edge of the diaphragm), there will be a combination of compression and shear waves.... I just can't see if happening in reality. A modal description is probably a better way to look at things, and this will reveal a low frequency mode that's the equivalent to the simple mass, spring, damper model of the driver (the pistonic behaviour) and then higher frequency modes (the breakup). The breakup modes are the ones that can lead to the ringing you talk about. Normally the designer will try and either not excite these modes (for example, by choice of coil position), damp these modes with lossy materials, or possibly there might be some modes that don't result in much sound radiation. Yes, there are designs that try and use the ringing of these modes. Most notably the BMR driver concept invented by NXT, the NXT DML loudspeaker, and I guess you could also throw in the densely modal cone drivers into the mix too: typically woven Kevlar. In all cases the reward for using these modes is higher output and wider directivity at high frequencies. The penalty is potentially in the evenness of the frequency and directional response.
Kind regards,
Jack.
Regarding (2.), I think I understand what you are describing regarding the methods of solving the wave equation. However, I'm not sure I'm understanding well your agument regarding the occurrence of wave propagation here "In all cases there should be wave-behaviour...": are you implying that wave propagation always happens, regardless of the ratio of box size to wavelenght? I still think that especially for a small box, wave propagation will occur only if a periodic excitation (like a wall under induced vibrations) is sufficiently rapid as to produce a wavelenght shorter than the box size and, on the contrary, if the excitation is too slow, the wavelenght will become larger and the compression-decompression of the contained air will be quasistatic. Do you think this is correct?
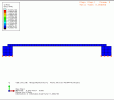
Regarding (3.), it was not my intention to imply that allowing waves to propagate through the cone/membrane is an efficient or correct method for designing a speaker. (I'm not a speaker designer and am certainly not qualified to stated something like that). I was only trying to say that wave propagation may also accur in the cone, not only in the air. I found in my files a very simple simulation I carried out many years ago with Abaqus, when working at a University in Spain, where I had to model for a project an elastic beam with some damping under a periodic central load (attached gif file), including elastic supports. Of course this is not a speaker cone, but the idea is similar. If the frequancy of the central loading had been much slower, static bending would have been observed instead of wave propagation.
Thanks again for your responses and best regards,
Jorge
Attachments
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,309
In general, this relates to dimensional behavior. For example in electronics, we often use lumped elements that are zero-dimensional for electrical circuits, where there is no concept of wave propagation and everything happens at once in some sense. For one-dimensional behavior, for example along long cable/high frequencies, we would use a transmission line model to capture the travelling and standing waves, and we would talk about characteristic impedance, reflection, and such. But there is no sudden jump from one situation to the other. At some point it just becomes necessary to transition to the 'next dimension up', because effects are not captured correctly. Sometimes we can opt for expanding on the 0D model and add some more components, using 'distributed components', and get some more bandwidth to the model, and that may be enough for what we are doing. It is the same thing that you have here: There is a quasi-static situation, where a closed box will have a constant pressure across all its volume (see also my post on Room Gain for something relevant to that), and as you go higher in frequency, you will see that a simple compliance (0D component) can no longer capture all effects that you see, and you need to consider waves. Same thing goes for the structural mechanics; masses and springs can be lumped together, but at higher frequencies we need to up the model to consider waves and modes.Thanks Jack and also René!
Regarding (2.), I think I understand what you are describing regarding the methods of solving the wave equation. However, I'm not sure I'm understanding well your agument regarding the occurrence of wave propagation here "In all cases there should be wave-behaviour...": are you implying that wave propagation always happens, regardless of the ratio of box size to wavelenght? I still think that especially for a small box, wave propagation will occur only if a periodic excitation (like a wall under induced vibrations) is sufficiently rapid as to produce a wavelenght shorter than the box size and, on the contrary, if the excitation is too slow, the wavelenght will become larger and the compression-decompression of the contained air will be quasistatic. Do you think this is correct?
Regarding (3.), it was not my intention to imply that allowing waves to propagate through the cone/membrane is an efficient or correct method for designing a speaker. (I'm not a speaker designer and am certainly not qualified to stated something like that). I was only trying to say that wave propagation may also accur in the cone, not only in the air. I found in my files a very simple simulation I carried out many years ago with Abaqus, when working at a University in Spain, where I had to model for a project an elastic beam with some damping under a periodic central load (attached gif file), including elastic supports. Of course this is not a speaker cone, but the idea is similar. If the frequancy of the central loading had been much slower, static bending would have been observed instead of wave propagation.
Thanks again for your responses and best regards,
Jorge
Last edited:
DaveBoswell
Member
Thanks @jackocleebrown and @René - Acculution.com for both of these very interesting and informative posts.
I think one thing that was not mentioned that I would like to confirm is that yes in fact the instant the cone commences to accelerate outwards, there is, as you would intuitively think, a compression of the air right in front of the cone, but then this compression naturally starts moving away from the cone at the speed of sound, and the velocity of the outbound compression and subsequent rarefaction waves is much higher than the peak velocity of the outbound cone. So by the time the cone is in constant velocity and then decelerates to zero velocity at the outbound limit, the initial compression caused by the accelerating cone has moved away from the face of the cone, which must then result in a rarefaction wave right behind it (which due to conservation of mass must be there in all cases where there is a fixed quantity of air molecules). Hence the reason why there is a rarefaction (or low pressure) at the instant the cone is at its maximum.
so for example, some back of envelope math:
where freq = 50Hz and
xmax = 20mm
cone distance travel for each cycle = 80mm
average cone velocity = 80mm / (1/50 s) = 4000 mm/s = 4 m/s
estimate peak velocity of 2x avg = 8m/s
whereas speed of wave propagation/sound =~ 345 m/s
So the outbound compression wave moves away from the accelerating cone at 2 orders of magnitude higher speed than the peak cone velocity.
Now when I think of it this way, it makes much more sense to me that by the time the cone reaches constant velocity and then decelerates, the bulk of the compression wave has "left the station" so to speak because it is travelling at a much higher velocity than the cone itself, so by extension, of course it leaves a negative wave when the cone stops and then reverses direction. Insert "aha moment" here.
Do I have this right?
I think one thing that was not mentioned that I would like to confirm is that yes in fact the instant the cone commences to accelerate outwards, there is, as you would intuitively think, a compression of the air right in front of the cone, but then this compression naturally starts moving away from the cone at the speed of sound, and the velocity of the outbound compression and subsequent rarefaction waves is much higher than the peak velocity of the outbound cone. So by the time the cone is in constant velocity and then decelerates to zero velocity at the outbound limit, the initial compression caused by the accelerating cone has moved away from the face of the cone, which must then result in a rarefaction wave right behind it (which due to conservation of mass must be there in all cases where there is a fixed quantity of air molecules). Hence the reason why there is a rarefaction (or low pressure) at the instant the cone is at its maximum.
so for example, some back of envelope math:
where freq = 50Hz and
xmax = 20mm
cone distance travel for each cycle = 80mm
average cone velocity = 80mm / (1/50 s) = 4000 mm/s = 4 m/s
estimate peak velocity of 2x avg = 8m/s
whereas speed of wave propagation/sound =~ 345 m/s
So the outbound compression wave moves away from the accelerating cone at 2 orders of magnitude higher speed than the peak cone velocity.
Now when I think of it this way, it makes much more sense to me that by the time the cone reaches constant velocity and then decelerates, the bulk of the compression wave has "left the station" so to speak because it is travelling at a much higher velocity than the cone itself, so by extension, of course it leaves a negative wave when the cone stops and then reverses direction. Insert "aha moment" here.
Do I have this right?
sam_adams
Major Contributor
- Joined
- Dec 24, 2019
- Messages
- 1,002
- Likes
- 2,447
An interesting paper on a method for the imaging of sound:
Schlieren Imaging Of Loud Sounds And Weak Shock Waves In Air Near The Limit Of Visibility - Michael John Hargather
Schlieren Imaging Of Loud Sounds And Weak Shock Waves In Air Near The Limit Of Visibility - Michael John Hargather
Would it be fair to say that one reason this transduction principle works so well (speaker output of recorded music sounds like music) is because microphones work on the same principle?
If so I guess my second question is - back in the 1800s, did they simply hook things up and found they worked, or did someone have to figure all of this out at the theoretical level, before we had any audio transducers at all?
If so I guess my second question is - back in the 1800s, did they simply hook things up and found they worked, or did someone have to figure all of this out at the theoretical level, before we had any audio transducers at all?
- Thread Starter
- #33
Thanks @jackocleebrown and @René - Acculution.com for both of these very interesting and informative posts.
I think one thing that was not mentioned that I would like to confirm is that yes in fact the instant the cone commences to accelerate outwards, there is, as you would intuitively think, a compression of the air right in front of the cone, but then this compression naturally starts moving away from the cone at the speed of sound, and the velocity of the outbound compression and subsequent rarefaction waves is much higher than the peak velocity of the outbound cone. So by the time the cone is in constant velocity and then decelerates to zero velocity at the outbound limit, the initial compression caused by the accelerating cone has moved away from the face of the cone, which must then result in a rarefaction wave right behind it (which due to conservation of mass must be there in all cases where there is a fixed quantity of air molecules). Hence the reason why there is a rarefaction (or low pressure) at the instant the cone is at its maximum.
so for example, some back of envelope math:
where freq = 50Hz and
xmax = 20mm
cone distance travel for each cycle = 80mm
average cone velocity = 80mm / (1/50 s) = 4000 mm/s = 4 m/s
estimate peak velocity of 2x avg = 8m/s
whereas speed of wave propagation/sound =~ 345 m/s
So the outbound compression wave moves away from the accelerating cone at 2 orders of magnitude higher speed than the peak cone velocity.
Now when I think of it this way, it makes much more sense to me that by the time the cone reaches constant velocity and then decelerates, the bulk of the compression wave has "left the station" so to speak because it is travelling at a much higher velocity than the cone itself, so by extension, of course it leaves a negative wave when the cone stops and then reverses direction. Insert "aha moment" here.
Do I have this right?
I understand the logic, but I'm afraid this isn't correct. For instance, it doesn't explain the difference between case 2 and case 3 (after all, both have the same speed of sound and exactly the same cone motion).
The key thing is that in case 2 the velocity of the air particles is parallel to one another. Look really closely at the black dots in case 2 and you will see they only move left to right. Acoustical pressure can only be due to particles being closer or further from their neighbour in the direction the wave travels.
In case 3 something subtly different happens. Look closely and you will see that the black dots move away from the cone in all directions. In addition to being close or further from other particles in the direction the wave travels, the particles are also more "spread out" perpendicular to the direction the wave travels. This is the mechanism that gives the negative pressure. I'll see if I can create some super slow zoomed in animations to try and highlight this more clearly.
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,309
I would'n try and think that way about it. It is the acoustic radiation impedance that sets the stage for the relationship between pressure and phase, with the wave propagation simply being a consequence.Thanks @jackocleebrown and @René - Acculution.com for both of these very interesting and informative posts.
I think one thing that was not mentioned that I would like to confirm is that yes in fact the instant the cone commences to accelerate outwards, there is, as you would intuitively think, a compression of the air right in front of the cone, but then this compression naturally starts moving away from the cone at the speed of sound, and the velocity of the outbound compression and subsequent rarefaction waves is much higher than the peak velocity of the outbound cone. So by the time the cone is in constant velocity and then decelerates to zero velocity at the outbound limit, the initial compression caused by the accelerating cone has moved away from the face of the cone, which must then result in a rarefaction wave right behind it (which due to conservation of mass must be there in all cases where there is a fixed quantity of air molecules). Hence the reason why there is a rarefaction (or low pressure) at the instant the cone is at its maximum.
so for example, some back of envelope math:
where freq = 50Hz and
xmax = 20mm
cone distance travel for each cycle = 80mm
average cone velocity = 80mm / (1/50 s) = 4000 mm/s = 4 m/s
estimate peak velocity of 2x avg = 8m/s
whereas speed of wave propagation/sound =~ 345 m/s
So the outbound compression wave moves away from the accelerating cone at 2 orders of magnitude higher speed than the peak cone velocity.
Now when I think of it this way, it makes much more sense to me that by the time the cone reaches constant velocity and then decelerates, the bulk of the compression wave has "left the station" so to speak because it is travelling at a much higher velocity than the cone itself, so by extension, of course it leaves a negative wave when the cone stops and then reverses direction. Insert "aha moment" here.
Do I have this right?
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,309
They knew the fundamentals of electrodynamics, and that a moving magnet could generate a field and such, but the more rigourous design work regarding getting a flat response came much later.Would it be fair to say that one reason this transduction principle works so well (speaker output of recorded music sounds like music) is because microphones work on the same principle?
If so I guess my second question is - back in the 1800s, did they simply hook things up and found they worked, or did someone have to figure all of this out at the theoretical level, before we had any audio transducers at all?
- Thread Starter
- #37
The tube is either infinite, or it's extremely long. Because of this, the change in the volume caused by the piston displacing forwards is insignificant. The final volume of the tube is approximately the same as the initial volume of the tube. No air particles have been added or removed from the tube, and the temperature hasn't changed. This means that once everything has settled down, the final pressure is the same as the initial pressure.One additional question now we are at it. Is there an easy way to explain why in case 2 the pressure inside the tube returns to to a pressure equal to the initial pressure before the wave exits the tube?
killdozzer
Major Contributor
This is just great. Thank you.
Do you have some subjective opinion, some assumption on why even people in audio business often fail to understand this? It seems rather obvious (or perhaps you just explained it well enough) that the furthest point in driver exclusion can be nothing other than a full stop even if for just a fraction of a second.
Do you have some subjective opinion, some assumption on why even people in audio business often fail to understand this? It seems rather obvious (or perhaps you just explained it well enough) that the furthest point in driver exclusion can be nothing other than a full stop even if for just a fraction of a second.
Last edited:
- Thread Starter
- #39
To try and explain the difference between case 2 and case 3 more clearly I've added some additional animations at the end of the first post.I understand the logic, but I'm afraid this isn't correct. For instance, it doesn't explain the difference between case 2 and case 3 (after all, both have the same speed of sound and exactly the same cone motion).
The key thing is that in case 2 the velocity of the air particles is parallel to one another. Look really closely at the black dots in case 2 and you will see they only move left to right. Acoustical pressure can only be due to particles being closer or further from their neighbour in the direction the wave travels.
In case 3 something subtly different happens. Look closely and you will see that the black dots move away from the cone in all directions. In addition to being close or further from other particles in the direction the wave travels, the particles are also more "spread out" perpendicular to the direction the wave travels. This is the mechanism that gives the negative pressure. I'll see if I can create some super slow zoomed in animations to try and highlight this more clearly.
- Thread Starter
- #40
Most trained acousticians would have studied radiation from compact sources into free-space at some point, but it's often done in a fairly abstract way using complex numbers. Mostly you find that velocity sources are used during teaching and there's not much discussion of flatness of transfer function or phase. Simply that a compact volume velocity source will generate spherically spreading waves in free-space that attenuate with the inverse of the radius. As an overview, that's all you need to know that the rest is there in the equations for people who need to apply things more rigorously.Do you have some subjective opinion, some assumption on why even people in audio business often fail to understand this? It seems rather obvious (or perhaps you just explained it well enough) that the furthest point in driver exclusion can be nothing other than a full stop even if for just a fraction of a second.
I think that pretty much all loudspeaker designers know very well that radiated pressure is proportional to acceleration (at least for a direct radiating speaker), one or two just might not have thought about the implicit phase relationship between pressure and cone displacement.
Finally, I think that it's a real skill/challenge to explain things in an accessible and easy to understand way. It's very easy to accidentally loose some precision in the process, especially if you're trying to make things intuitive. So I'm certain there's a lot of that going on too with this particular subject.
Similar threads
- Replies
- 68
- Views
- 8K
- Replies
- 15
- Views
- 4K
- Replies
- 12
- Views
- 2K
- Replies
- 133
- Views
- 40K