This post provides a quick comparison of how a distortion percentage relates to dynamic range in dB. That is, if an amplifier has 1% distortion, what does that mean? How soft (or loud) is 1%?
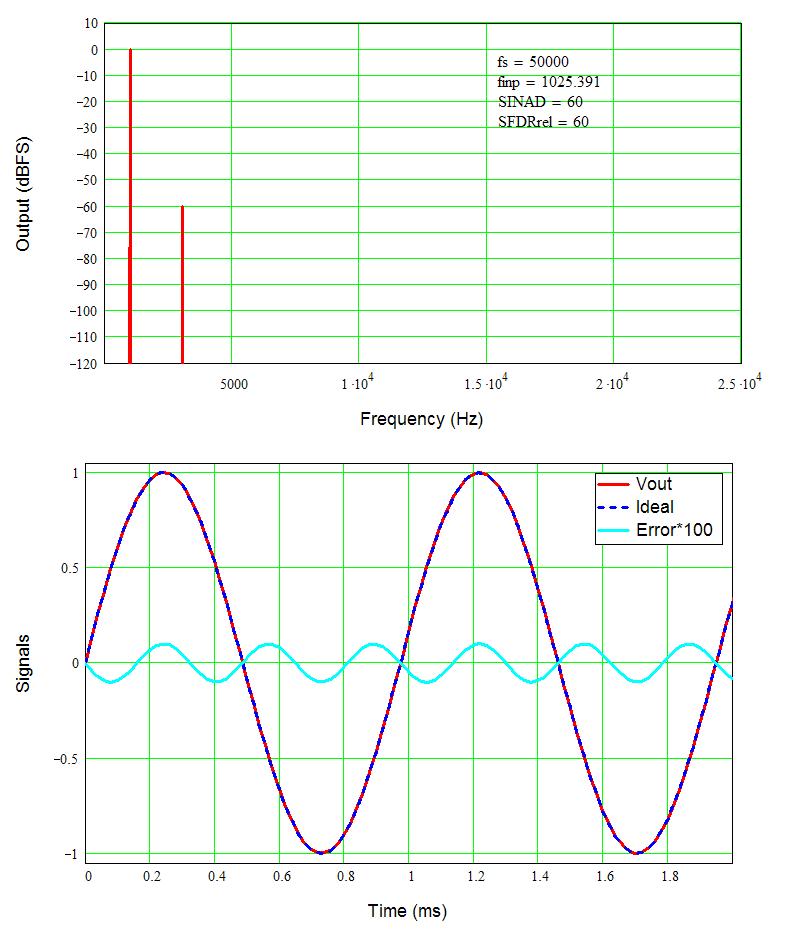
Figure 1 shows a 1 kHz voltage signal with 1% second harmonic distortion (HD2) added. The spectral analysis (FFT, fast Fourier transform) shows the second harmonic at 40 dB below (-40 dB) the (0 dB) signal. So, 1% distortion is 40 dB below the signal level. Recall that dB = 20log(x), 1% is 1/100 = 0.01, and 20log(0.01) = -40 dB. Aside: Power goes as 10log(x), so 1% distortion in power (Watts) is only -20 dB. In SPL (dB/W), 20 dB is about the difference between say a pretty loud sound (80 dB) and a normal conversational volume (60 dB). Since we are in voltage (maybe a preamplifier output before the power amp), 40 dB takes you from that loud sound down to a fairly quiet room, say a library.
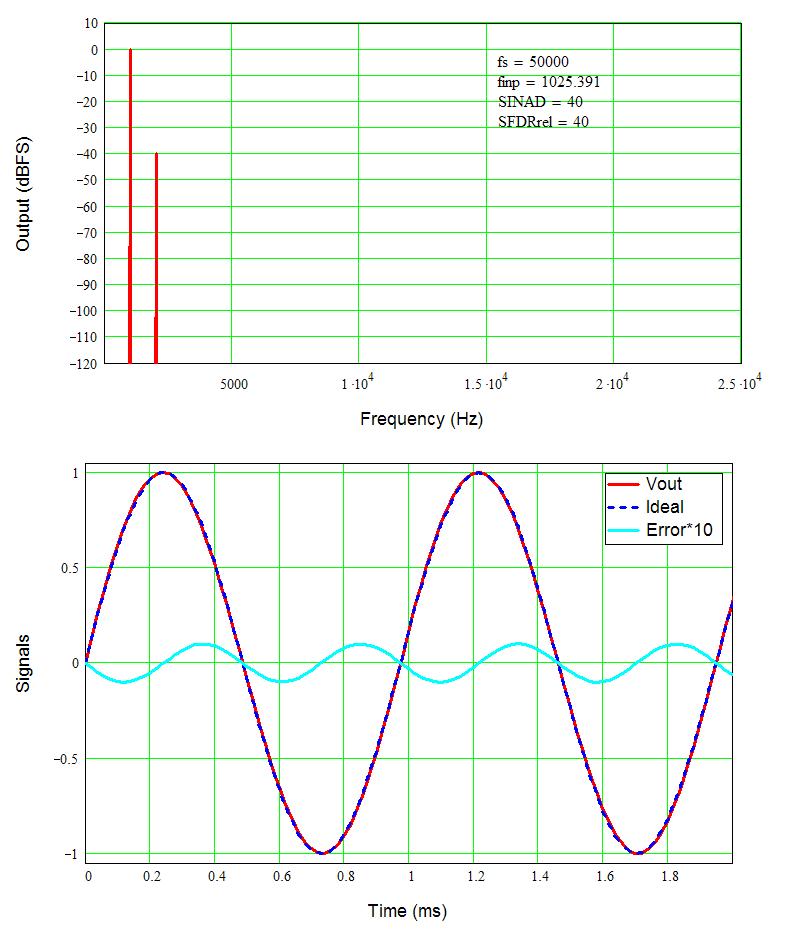
The lower plot shows an ideal sine wave, the signal with 1% distortion, and the difference (error) signal multiplied by 10 to make it easier to see. By eye, I cannot see any difference in the ideal input signal and output with 1% distortion (Vout). Because the error is purely second harmonic distortion, notice there are twice as many cycles in the error as in the input signal.
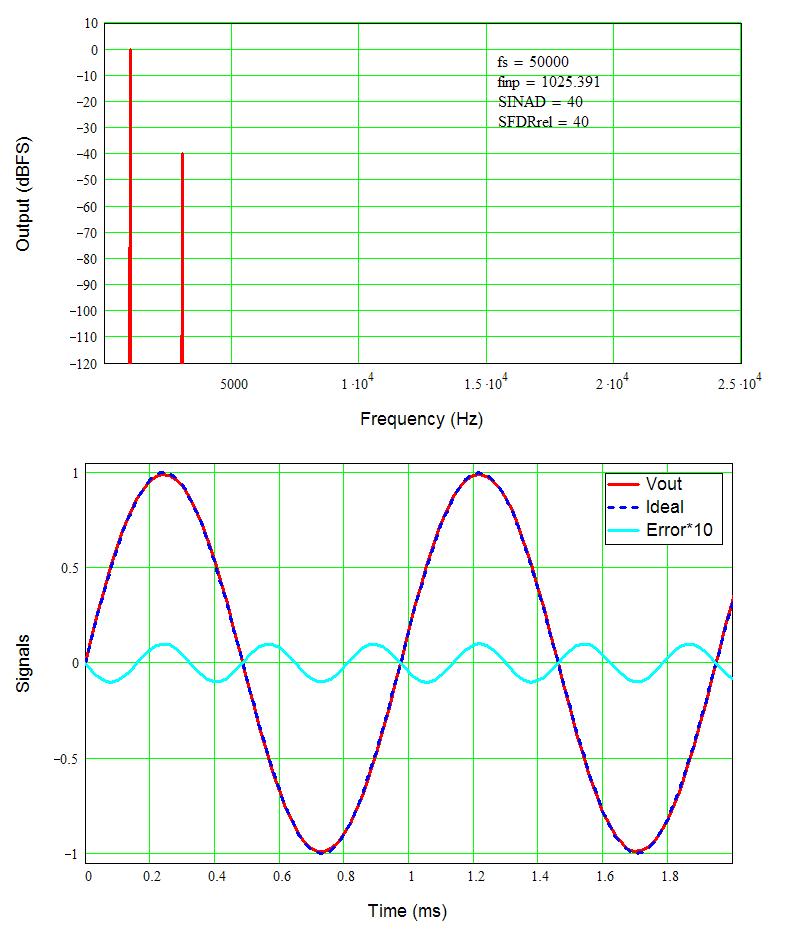
The figure below shows the same 1% distortion but now it is third harmonic distortion (HD3). The HD3 spur is -40 dB, but notice there are now three error cycles for each full cycle (0-up-0-down-o) of the signal. And again, I can’t see anything by eye (maybe you can).
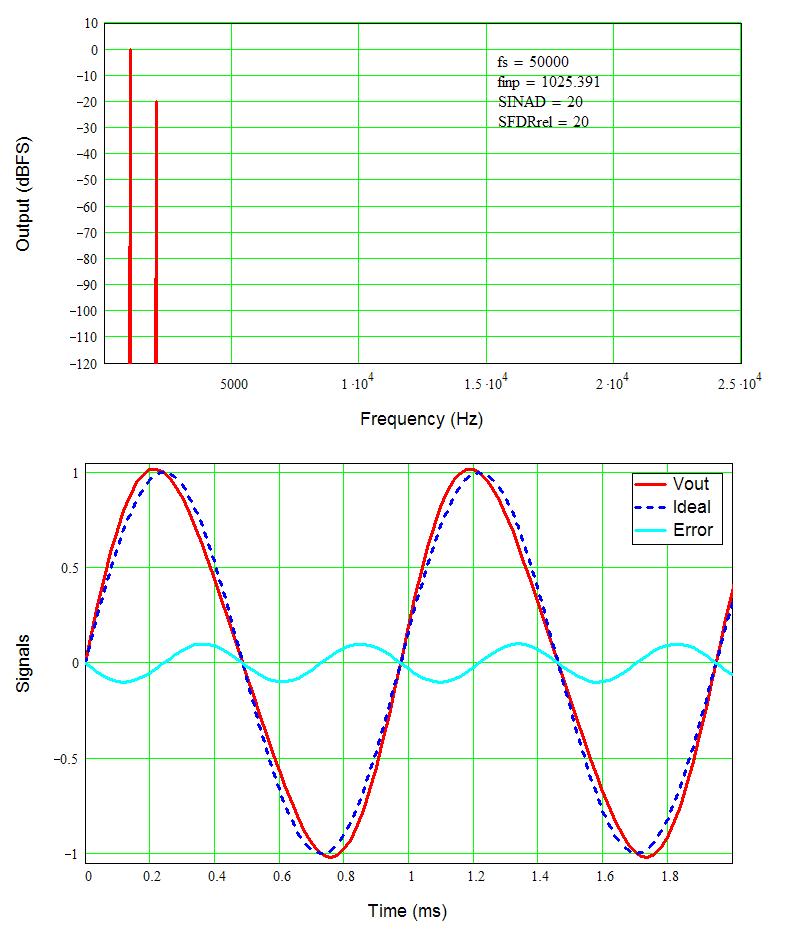
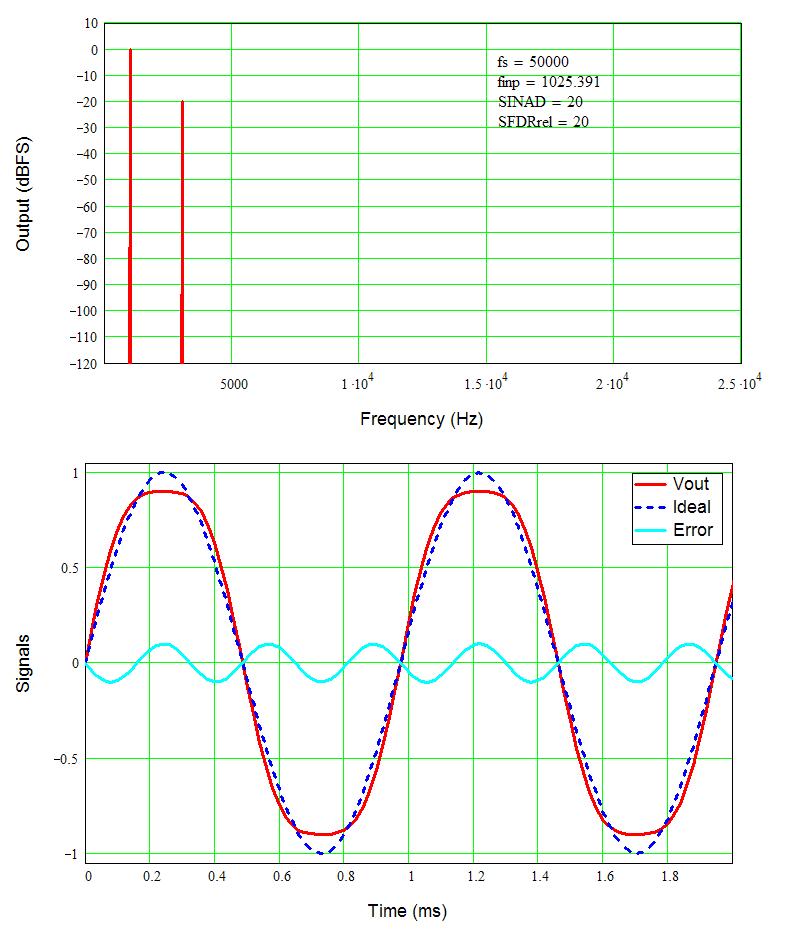
Just for grins, and for something to see, the following two pictures show 10% HD2 and HD3. As expected the harmonic terms are now only 20 dB below the signal. What is interesting is how the high level of distortion changes the look of the waveforms. Second harmonic distortion does not change the picture too much, but third harmonic distortion causes the peaks to flatten, sort of like a soft square wave. Even harmonics tend to sound more pleasant than odd harmonics, adding a bit of edge to the sound while odd harmonics create a raspy buzz.
Last is a figure showing 0.1% HD3, with a spur 60 dB below the signal. A factor of ten in distortion changes the level by 20 dB (in voltage; a 10x change in power is 10 dB).
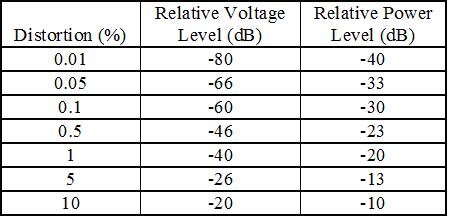
Finally, here’s a table showing the relationship among distortion in percent and dB in voltage (or current) and power. The dominant source of distortion in most systems is the speakers, which often run 1% or more in the midrange even for good ones, and 10% or more for large low-frequency signals. Amplifiers usually run in the 0.1 – 1% range, and preamps often 0.01% or better.
Hopefully this will help relate those distortion percentages to the dB specifications used for SNR, SPL, and so forth.
--- On to IMD ---
A previous post discussed harmonic distortion (HD), but to most people intermodulation distortion (IMD) is far more objectionable. Why? Because IMD generates tones that are not harmonically related to the input signals, and these tones “stick out” more than tones that are harmonics of the input tones. They sound “off” to our ears.
As an example, I created two tones at around 523 Hz (C above middle C on a piano) and 661 Hz (the E above, the root and third of a major chord). I added 0.1 % second- and third-order distortion terms (x^2 and x^3) and plotted the spectrum.
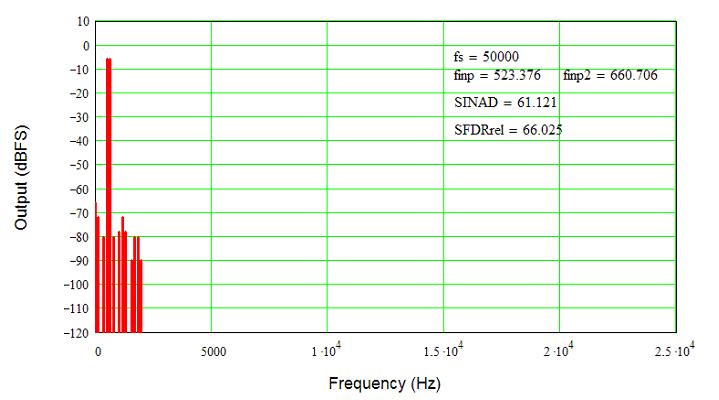
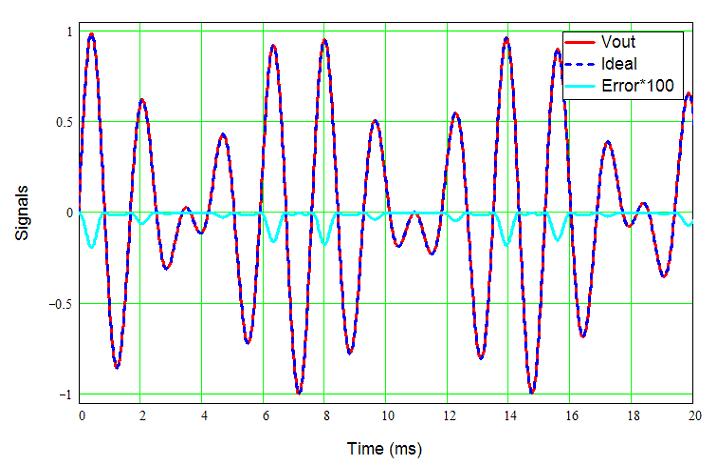
You can see the two signal tones at -6 dB, and a group of distortion spurs (tones) around the signal. I used -6 dB (0.5 full-scale) because two signals added will peak at 0 dB when they are each at one-half full-scale. You can see that in the next picture, which shows a few cycles of the signal. The funny-looking waveform is a result of the two signals mixing together, adding and subtracting from each other at different times. Even though each signal alone would only reach 0.5, together they reach 1.0 when they are in phase so both signals add. The error signal is multiple by 100 to make it easier to see; otherwise, the 0.1 % error would be essentially invisible by eye.
Below is a zoom showing the bunched signals, and a table of all the frequencies present. Not only do we have harmonics of each signal, at 2x and 3x the fundamental tones, but also intermodulation sum and difference terms. That means that we get C and E, and their second and third octaves, but also a tone a little over high D, a little below a low C# from the second-order IMD. The third-order IMD gives back the fundamental tones (but in general out of phase, causing amplitude modulation), and tones around a couple of (lower and higher) G’s (not too bad), Bb (oops), and a strange tone about half-way between Ab and A (what?) As a matter of fact, none of the IMD tones lie exactly on a piano note. These added tones add dissonance not in the original chord structure, and our ears are pretty good at picking out this dissonance. Yuck.

So, IMD creates non-harmonic tones, tones that do not lie in the chord, and that sounds bad. One other note: IMD tones are actually higher in magnitude than HD tones. Theoretically, IMD-2 tones are 6.021 dB higher than HD-2 tones, and IMD-3 tones are 9.542 dB above the corresponding HD-3 tones. Adding insult to injury… This is another reason IMD is more important than HD in the real world.
The derivation of all this is straight-forward but tedious. Take a couple of signals represented by Vin=sin(2*pi*f1*t)+sin(2*pi*f2*t), then build a function using
Vout = Vin + HD2*Vin^2 + HD3*Vin^3
After expanding out the terms and plugging in various trig identities you will find the terms in the table above, and the relation between HD and IMD amplitudes.
Hope this is useful - Don
Figure 1 shows a 1 kHz voltage signal with 1% second harmonic distortion (HD2) added. The spectral analysis (FFT, fast Fourier transform) shows the second harmonic at 40 dB below (-40 dB) the (0 dB) signal. So, 1% distortion is 40 dB below the signal level. Recall that dB = 20log(x), 1% is 1/100 = 0.01, and 20log(0.01) = -40 dB. Aside: Power goes as 10log(x), so 1% distortion in power (Watts) is only -20 dB. In SPL (dB/W), 20 dB is about the difference between say a pretty loud sound (80 dB) and a normal conversational volume (60 dB). Since we are in voltage (maybe a preamplifier output before the power amp), 40 dB takes you from that loud sound down to a fairly quiet room, say a library.
The lower plot shows an ideal sine wave, the signal with 1% distortion, and the difference (error) signal multiplied by 10 to make it easier to see. By eye, I cannot see any difference in the ideal input signal and output with 1% distortion (Vout). Because the error is purely second harmonic distortion, notice there are twice as many cycles in the error as in the input signal.
The figure below shows the same 1% distortion but now it is third harmonic distortion (HD3). The HD3 spur is -40 dB, but notice there are now three error cycles for each full cycle (0-up-0-down-o) of the signal. And again, I can’t see anything by eye (maybe you can).
Just for grins, and for something to see, the following two pictures show 10% HD2 and HD3. As expected the harmonic terms are now only 20 dB below the signal. What is interesting is how the high level of distortion changes the look of the waveforms. Second harmonic distortion does not change the picture too much, but third harmonic distortion causes the peaks to flatten, sort of like a soft square wave. Even harmonics tend to sound more pleasant than odd harmonics, adding a bit of edge to the sound while odd harmonics create a raspy buzz.
Last is a figure showing 0.1% HD3, with a spur 60 dB below the signal. A factor of ten in distortion changes the level by 20 dB (in voltage; a 10x change in power is 10 dB).
Finally, here’s a table showing the relationship among distortion in percent and dB in voltage (or current) and power. The dominant source of distortion in most systems is the speakers, which often run 1% or more in the midrange even for good ones, and 10% or more for large low-frequency signals. Amplifiers usually run in the 0.1 – 1% range, and preamps often 0.01% or better.
Hopefully this will help relate those distortion percentages to the dB specifications used for SNR, SPL, and so forth.
--- On to IMD ---
A previous post discussed harmonic distortion (HD), but to most people intermodulation distortion (IMD) is far more objectionable. Why? Because IMD generates tones that are not harmonically related to the input signals, and these tones “stick out” more than tones that are harmonics of the input tones. They sound “off” to our ears.
As an example, I created two tones at around 523 Hz (C above middle C on a piano) and 661 Hz (the E above, the root and third of a major chord). I added 0.1 % second- and third-order distortion terms (x^2 and x^3) and plotted the spectrum.
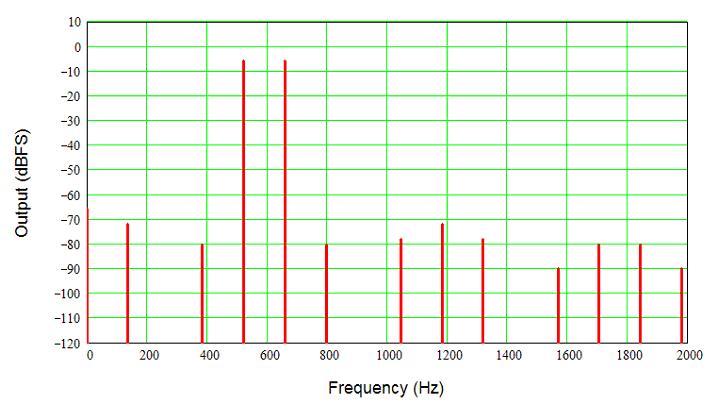
You can see the two signal tones at -6 dB, and a group of distortion spurs (tones) around the signal. I used -6 dB (0.5 full-scale) because two signals added will peak at 0 dB when they are each at one-half full-scale. You can see that in the next picture, which shows a few cycles of the signal. The funny-looking waveform is a result of the two signals mixing together, adding and subtracting from each other at different times. Even though each signal alone would only reach 0.5, together they reach 1.0 when they are in phase so both signals add. The error signal is multiple by 100 to make it easier to see; otherwise, the 0.1 % error would be essentially invisible by eye.
Below is a zoom showing the bunched signals, and a table of all the frequencies present. Not only do we have harmonics of each signal, at 2x and 3x the fundamental tones, but also intermodulation sum and difference terms. That means that we get C and E, and their second and third octaves, but also a tone a little over high D, a little below a low C# from the second-order IMD. The third-order IMD gives back the fundamental tones (but in general out of phase, causing amplitude modulation), and tones around a couple of (lower and higher) G’s (not too bad), Bb (oops), and a strange tone about half-way between Ab and A (what?) As a matter of fact, none of the IMD tones lie exactly on a piano note. These added tones add dissonance not in the original chord structure, and our ears are pretty good at picking out this dissonance. Yuck.
So, IMD creates non-harmonic tones, tones that do not lie in the chord, and that sounds bad. One other note: IMD tones are actually higher in magnitude than HD tones. Theoretically, IMD-2 tones are 6.021 dB higher than HD-2 tones, and IMD-3 tones are 9.542 dB above the corresponding HD-3 tones. Adding insult to injury… This is another reason IMD is more important than HD in the real world.
The derivation of all this is straight-forward but tedious. Take a couple of signals represented by Vin=sin(2*pi*f1*t)+sin(2*pi*f2*t), then build a function using
Vout = Vin + HD2*Vin^2 + HD3*Vin^3
After expanding out the terms and plugging in various trig identities you will find the terms in the table above, and the relation between HD and IMD amplitudes.
Hope this is useful - Don
Last edited:
