Floating-Point ADC System

[DonH56]

Here is an attempt to show how a floating-point ADC system might benefit a field recorder (or other device) needing to cover a wide dynamic range with better performance than a single ADC. The floating-point ADC system comprises four different gain stages (amplifiers) with switches into the ADC. The signal input Vin is applied to all four amplifiers simultaneously. The DSP determines which switch (gain stage) to use based upon the ADC’s (digital) output signal. It probably also performs calibration to ensure precise alignment among the four gain stages. The gain control setting is the exponent, and ADC output bits are the mantissa, of the floating-point output.

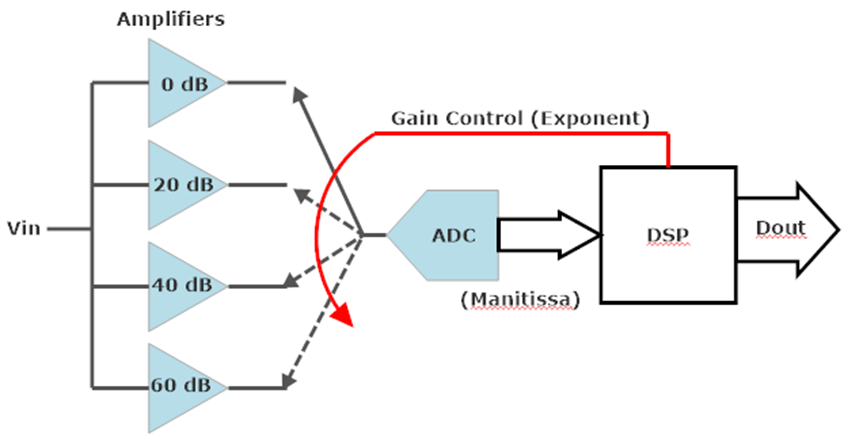
A gain of 20 dB is a factor of 10, so if the ADC has a full-scale range of 1 Vpk then the input would be [1, 0.1, 0.01, 0.001] Vpk to apply 1 Vpk at the ADC’s inputs for each gain stage from 0 to 60 dB. That is, each gain-of-20 dB stage means an input 1/10 smaller will be amplified to 1 Vpk, the ADC’s full-scale range. For this example, a 16-bit ADC is designed to have -100 dB THD for a full-scale signal and quantization noise sets the SNR to around 98 dB (ideal).

Now apply four signals ranging from full-scale (1 Vpk) down to 1 mVpk (-60 dB relative to full scale) in 20 dB (1/10th) steps and generate the results as if there was a single ADC with no gain stages. No gain switching, no floating-point operation.

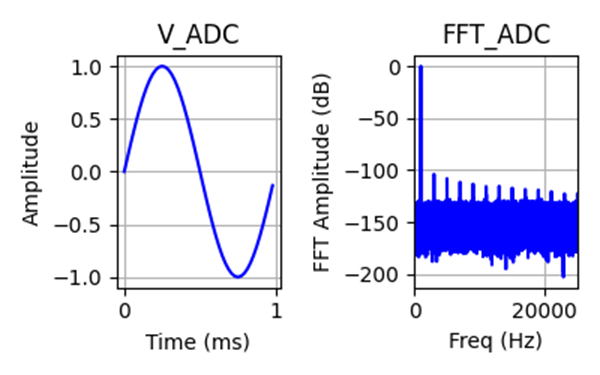
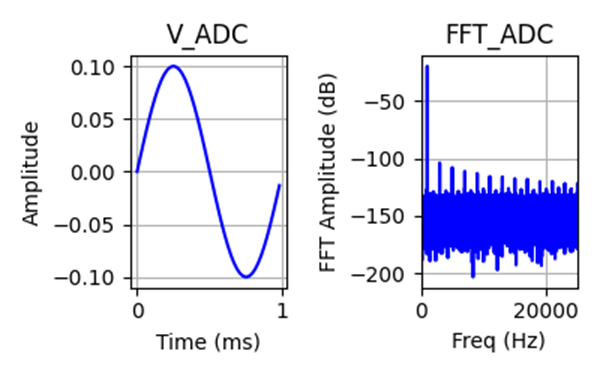
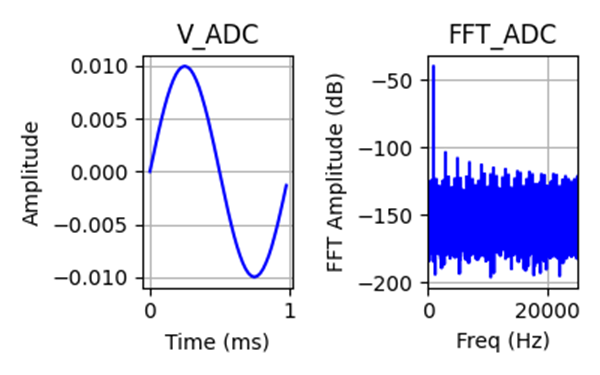
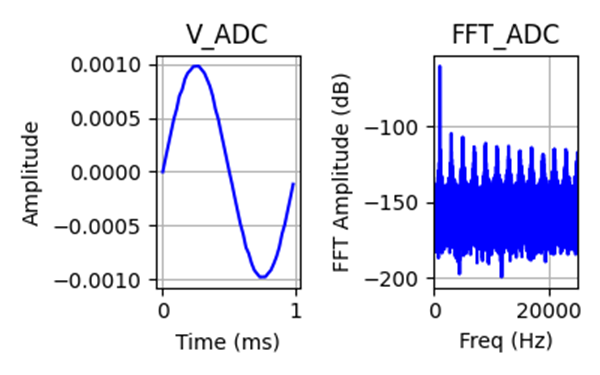
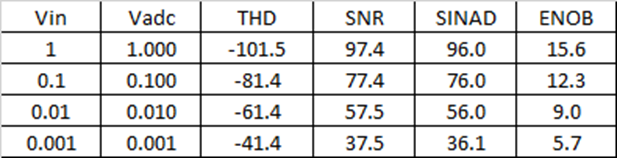
As the signal gets smaller, it approaches the noise and distortion floor of the ADC, so the effective number of bits (ENOB) drops. At 1 Vpk, there is only slight reduction in performance from an ideal 16-bit converter, but as the signal gets smaller, the SINAD shows 20 dB drops tracking the signal level, which is reflected in the ENOB the ADC delivers to the system.

Now to implement floating-point operation, switch gain as the signal drops, adding 20 dB (10x) gain at each step and thus maintaining full-scale input to the ADC. Not surprisingly, the performance is now the same for each input level, since all the gain stages are ideal (no added noise or distortion). In practice, they will add a little noise and distortion of their own, but the results will still be much better performance than using a single ADC. I only show one plot since, due to the extra gain, the other three are the same.

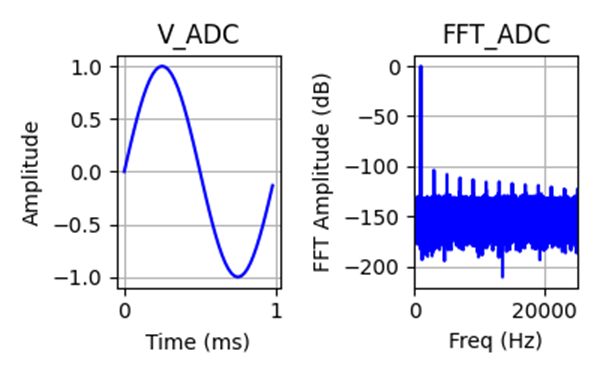
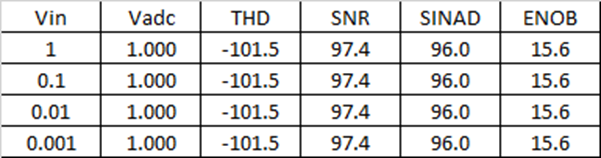
For these test signals, the floating-point system provides 15.6 bits for each signal, compared to a range from 15.6 down to only 5.7 bits without switching gain before the ADC. If the signal falls between gain ranges, you will lose performance (effective bits) just as with a regular ADC, but since 20 dB is about 3 bits, you only lose about 3 bits (from ~16 down to ~13 ENOB) before switching in more gain.

If you exceed the maximum input, the ADC will still clip, so designers may choose full-scale to provide headroom beyond what the input signal can reach (e.g. maximum output from the microphone). At the low end, as the signal drops below 1 mVpk, the number of bits will fall off conventionally, losing about one bit each time the signal drops in half (6 dB). That is, at 0.25 mVpk (1/4 the signal), or 12 dB lower than the minimum that can be amplified to full scale for the ADC, the best the ADC can produce is 14 effective bits (16 – 2 = 14 ENOB).

So, for a range from 1 mVpk to 1 Vpk, we maintain ADC performance of 13 to 16 bits (ideally) using this floating-point system. Beyond 1 Vpk, the system will still clip, and below 1 mVpk the system will lose 1 bit each time the signal falls in half (same as any ADC). In contrast, a single (non-floating-point) 16-bit ADC would range from about 6 to 16 effective bits over that same 1 mVpk to 1 Vpk range.

HTH – Don

 

[voodooless]

Thanks Don! Your murdered your attachments though

 

[DonH56]

Thanks Don! Your murdered your attachments though

You were too quick, they were in progress. I copied from another thread and the attachments did not come through so I had to edit them back in.

 

[AdamG]

You were too quick, they were in progress. I copied from another thread and the attachments did not come through so I had to edit them back in.

Moved to Audio Reference Library. As always excellent work Don. Thank you Sir.

 

[voodooless]

So, you have 4x ~16 usable bits, 20 db apart, so about 156 dB DNR, or about 26 bits integer, right?

 

[DonH56]

So, you have 4x ~16 usable bits, 20 db apart, so about 156 dB DNR, or about 26 bits integer, right?

Yes, although real-world noise and distortion will reduce the total (realizable) dynamic range.

 

[Berwhale]

Thanks Don, this took me back over 30 years to my college days which was the last time I actually played with an ADC (on an MC68HC11 microcontroller development board).

 

[voodooless]

Yes, although real-world noise and distortion will reduce the total (realizable) dynamic range.

Obviously. How well can you actually calibrate these ADCs? How does one do that?

I would do something like this (just off the cuff here): Essentially, all of them get the same (scaled) signal, so as long as none of the ADCs clip, you can assume that the average (scaled) value between them is the value to calibrate towards. You can then average these over multiple samples to reduce error further.

 

[DonH56]

Obviously. How well can you actually calibrate these ADCs? How does one do that?

Usually to within one lsb, or maybe a few lsbs, and there are many schemes to do so. But beyond the scope of this introductory article. You could use a calibrated signal source (leaving aside of how you calibrate the calibrator) and adjust the analog gain stages. With 20 dB stages you could send the same signal in, or use a calibrated stepped attenuator, and measure the signal using the DSP to align the codes (probably simpler than tweaking analog gains using variable currents, voltages, or whatever). You could provide some overlap among the gain stages and let the DSP calculate it from a known signal, etc. You could trim the gain and reference stages for the ADC during package testing, etc. Typically for precision ADCs (among other things) you must calibrate after packaging as packaging stress can shift thresholds.

Different schemes may use different calibration schemes. With this example, it is all about calibrating the gain stages so they are "perfect", either by adjusting their gains and offsets in a programmable-analog fashion, or by applying a numerical correction to the ADC's output using the DSP. I suspect the latter is more common (and usually easier and more precise). With the example in the floating-point thread, using separate amplifiers and ADCs, applying a signal or three and using the DSP to calculate the differences and align the ADC outputs makes the most sense to me.

I would do something like this (just off the cuff here): Essentially, all of them get the same (scaled) signal, so as long as none of the ADCs clip, you can assume that the average (scaled) value between them is the value to calibrate towards. You can then average these over multiple samples to reduce error further.

In a real-time system presented with unknown signals you cannot average, but sure you could use some sort of averaging during the calibration process to reduce the effects of noise. Long ago what I did was to create a very precise on-chip attenuator using laser-trimmed resistors to create a reference signal for each gain setting (measured during final test) and calibrated to that. These days on-chip processing is relatively cheap so I would skip the laser trimming, measure during final test, and program the calibration values for future use (in e-fuses or other memory -- some may use an off-chip EPROM or NVRAM to store the values).

Having some extra ADC bits for overlap and gain tweaks makes life much easier, natch. One of the biggest issues with any calibration scheme is how well the circuit holds calibration over things like power supply, temperature, other environmental variations, and time... I have worked on chips that monitored things like supply voltage and temperature and would force a recalibration if they drifted too far.

 

[voodooless]

In a real-time system presented with unknown signals you cannot average,

Why not? You know that whatever values you get are the same thing. So you can converge to each other. You’ll obviously need multiple samples to lower the error.

 

[DonH56]

Why not? You know that whatever values you get are the same thing. So you can converge to each other. You’ll obviously need multiple samples to lower the error.

I do not want to divert too much here. Yes, all paths get the same input, but to average you need multiple known samples, otherwise the system will not know the "proper" values to use since they are constantly changing. There is also the dynamic range problem; depending upon the architecture, it may not be possible to calibrate using a single signal value, since you will be over or under driving the ADC through various gain paths. IME you use static (DC) values or a fixed signal (or set of signals) for calibration. I am not sure I am understanding your argument.

 

[DVDdoug]

Zoom makes a floating-point recorder.

From my limited understanding of how modern ADCs & DACs work, it's probably not that difficult and I wouldn't be surprised if it became more common.

It would be nice to have some headroom. There will still be voltage limits so you won't get the full 32-bit floating-bit range, but clipping at +12 or +20dB would be cool. And of course, on the low-end you're still noise-limited.

And if you need to limit to 0dB (for broadcast or live use, etc.) you could limit digitally. ...You can't properly limit after the ADC is hard-clipped If you want to do that with a normal ADC, you need a hardware-limiter in front of the ADC.

 

[voodooless]

I am not sure I am understanding your argument.

Clearly So let me try again, and obviously this is all just a fun mind experiment and not super relevant to the topic, but nevertheless… So the idea is to calibrate on-the-fly, using real dynamic signals. Yes, you’ll need a multitude of samples to make sure you have enough data from all the ADCs in their un-overloaded state. So in some cases you can only use two or three ADCs for a particular sampled value. But I think with a bit of clever math you can have all ADCs converging towards one calibration. Yes, this is still relative, so if you want an absolute calibration of say x V is y dBfs, you’ll only need to do that only once for the whole stack of ADCs all the way at the end. For this you’ll obviously need a stable signal.

 

[DonH56]

Clearly So let me try again, and obviously this is all just a fun mind experiment and not super relevant to the topic, but nevertheless… So the idea is to calibrate on-the-fly, using real dynamic signals. Yes, you’ll need a multitude of samples to make sure you have enough data from all the ADCs in their un-overloaded state. So in some cases you can only use two or three ADCs for a particular sampled value. But I think with a bit of clever math you can have all ADCs converging towards one calibration. Yes, this is still relative, so if you want an absolute calibration of say x V is y dBfs, you’ll only need to do that only once for the whole stack of ADCs all the way at the end. For this you’ll obviously need a stable signal.

There are dynamic calibration schemes. I'll let you write the next article.

 

[alc]

This is actually a fairly old technique that was used more often when ADCs had fewer bits. There are a few gotchas to watch for,

1. When you have a large signal, the stages with gain are going to be in severe overload. If you use large series Rs for current limiting and clamps, you add Johnson (thermal ) noise. You also dump current into power supplies.

2. The accuracy of the 20dB amplifiers need to be very good.

3. The high frequency performance of the high gain stages will suffer from insufficient gain-bw product at some point,

4. Often this method used a pair of ADCs where you overlap adjacent ranges. This means you have two samples separated by 20dB in your example. You rarely need all the dynamic range at the same time. I would probably make gains a perfect power of 2 so that you can combine conversions easier and see how the two combine better. Sigma Delta convertors work best for this kind of application so that the antialiasing filters are essentially identical.

I am not trying to be a naysayer, just like every other solution, there are compromises.

Al

 

[MC_RME]

4. I have never seen the version described in the OP, only the one with multiple ADCs. And the reason seems to be obvious: you can't change between the 4 input amps in real-time without getting clicks and other artefacts - it's a fully analog solution in that part. The multiple ADC solution (one ADC per input amp) however uses a DSP to combine the multiple digital data streams, which is easily possible without such errors in sample accuracy.

 

[restorer-john]

I have never seen the version described in the OP, only the one with multiple ADCs. And the reason seems to be obvious: you can't change between the 4 input amps in real-time without getting clicks and other artefacts - it's a fully analog solution in that part.

The system described by @DonH56 is used in audio analyzer front ends for autoranging to keep the applied signal in the A/D's linearity range. Not just gain, but extreme attenuation also.

 

[MC_RME]

But that would look a bit different, and I doubt they use 32 bit float internally to set the various gains for the hardware front-end.

 

[Blumlein 88]

What is it that Sound Devices do in their products that claim a super wide dynamic range, and that you can record without every worrying about clipping being possible? I'd thought it was what MC_RME is describing, but then it just didn't do well in testing by Amir here.

 

[Hayabusa]

It would never work well this way. The multiplexer would generate audible glitches.
If each attenuation/gain path has its own ADC it could work.
The dsp would need to merge the synchronous ADC channels.
Having all these channels available in parallel also makes calibration more easy.