Composition of a Square Wave (important!)

[amirm]

Author: our resident expert, DonH50 (above title mine )

Building a Square Wave
Since I used a square wave as an example in another thread, I realized that what is common knowledge for hairy-knuckled engineers such as I and high-brow scientists like some of the other folk here, may still be mysterious to many audiophiles. I thought it might be worth recreating a simple set of plots that shows how we can make a square wave from a bunch of simple sine waves, i.e. single frequency tones.

For starters, we must realize that any signal can be represented by an infinite sum of single tones of the right amplitude and phase. This is a fundamental principle upon which all signal processing is based. Problems arise, like in many areas of life, when reality hits the theory... In this case, it's impossible for a real system to have infinite frequency response, sampled or not, and of course getting all those tones' amplitudes and phases just right when we add them up is a real problem. Sampling means we only have a limited bandwidth to work with, so the number of frequencies we can sum is fixed by the fundamental signal frequency and the sampling frequency.

A square wave is comprised of an infinite sum of only odd harmonics of the signal. That is, a 1 kHz square wave includes 1 kHz, 3 kHz, 5 kHz, and so on out to infinity. No even harmonics! The amplitude of the odd harmonics decreases as the ratio 2/(n*pi) where n is the harmonic number and pi = 3.14159... (that old circle number). So, the third harmonic is only 1/3 the amplitude of the fundamental, the fifth is 1/5, etc. It doesn't take a whole lot of harmonics before we can't really see much difference between an ideal square wave and one with only a few components. Digital systems routinely work with limited bandwidth to reduce noise. Noise just keeps getting larger as you increase the system bandwidth, so it makes sense to use as little bandwidth as required to capture the signal and thus maximize the SNR.

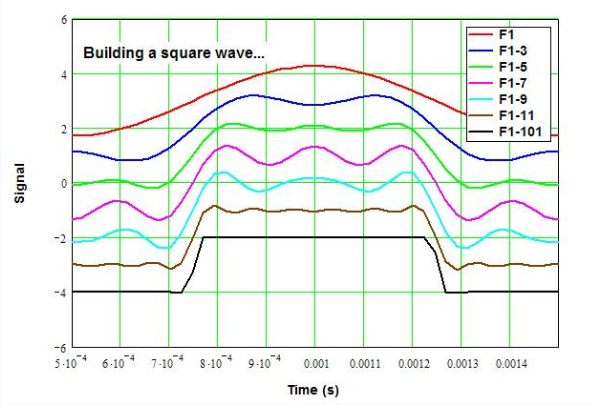
For this example, I went back to a 1 kHz signal, and started added harmonics as required to build a square wave. The top plot is the 1 kHz sine wave, a nice single tone. I added a bit of 3rd harmonic, and you can see the top is already starting to flatten. Added in the 5th, and it actually starts to look like a square wave! As I add the 7th and 9th harmonic terms, it looks like the flat top ripple is a little worse, but the edges are starting to shape up now. By the time I add in the first 11 terms we have a pretty decent square wave. The bottom curve is the first 101 terms (fundamental plus 100 harmonics) and is about as close to a perfect square wave as made sense to me to plot.

This next plot shows the single (fundamental) 1 kHz tone and sums to the 3rd, 5th, and 101st harmonic. You can see that even with only 5 terms the edges are nearly as fast as using 101, at least to the eye (and usually to the ear as well).

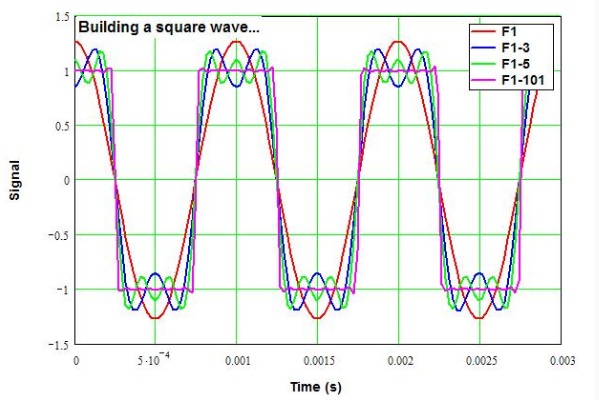
What does this mean? Well, there aren't many square waves in music, but there are a lot of harmonics. If we were to reproduce a square wave, and decide we need at least 5 terms, then the highest square wave we can produce on a CD is about 20 kHz/5 = 4 kHz.

Hope this is useful! - Don

 

[DonH56]

I was doing some testing at work and dealing with Gibbs Effect and remembered this old post. One thing that happens on the measurement side of things is that we filter our square waves, usually to bandlimit the signal to the device under test. That means we roll off the higher-frequency part of our square wave. Now, if we use a simple one-pole (e.g. RC) filter, then the harmonic roll-off is more or less aligned with the frequency content of a square wave and we get a smooth result. However, using higher-order filters (typical), means we are reducing the higher frequencies at greater than a 1/f slope, and the end result is we get a square wave that looks like the picture with only a few lower-frequency components.

If we use a steep filter than rolls off everything over the seventh harmonic, then we'll generate a signal that looks like the "F1-7" curve in the first plot above. Notice the waveform now looks like it has overshoot and ringing, but in fact the shape is because we filtered out the higher frequencies. This is not due to some component failure or phase margin issue, but simply because we filtered our "ideal" square wave so it no longer has all the frequencies needed to create that perfect flat top and sharp edges.

This is something we who do testing and measurements need to keep in mind lest we chase "ringing" in our designs that is not really there (don't ask how I know this). In my case, running the output of a 70 GHz clock signal into a 33 GHz oscilloscope resulted in Gibbs ringing, and sure enough I chased my tail for a bit looking for mismatches and such before slapping my head and remembering the basics.

Historical context (looked it up, memory not that good, and not quite old enough to be there): This was first noted by Henry Wilbraham in 1848 based on adding sine waves to create a square wave, essentially the same as I did in the first post. He used pencil and paper, natch, while my lazy self used Mathcad. It is called Gibbs Effect (effect, phenomena, ringing, etc.) because some years later (1898) J Willard Gibbs noted the same thing but using Fourier analysis when he truncated (filtered) the Fourier expansion of a square wave and saw the "ringing" that resulted.

For further reading, I had this recent article bookmarked, and there are many others: https://www.signalintegrityjournal....avoid-gibbs-ringing-artifacts-in-measurements When I realized what was happening, I remembered the article, after the fact (natch).

 

[solderdude]

Why does a FIR filter have the 'logical' Gibbs phenomenon (before and after a transition) but an IIR filter only after the transition ?

 

[egellings]

Excellent demo of square wave structure! I understood this idea before I saw this, but this is the best presentation I've seen yet. Bravo!

 

[dc655321]

Why does a FIR filter have the 'logical' Gibbs phenomenon (before and after a transition) but an IIR filter only after the transition ?

FIR filters are symmetric or anti-symmetric.
IIR filters are one sided, causal.

 

[solderdude]

I know but you can put a squarewave through such a filter and in that case the squarewave doesn't look like the familiar symmetric Gibbs effect.
Instead the parts of the 'ringing' where it is absent seems to have added to the other edge.

I know... this can be explained by math I don't understand but would like to see a 'simple' to understand explanation for the 'move' of the ' ringing'.

 

[DonH56]

Why does a FIR filter have the 'logical' Gibbs phenomenon (before and after a transition) but an IIR filter only after the transition ?

Handwaving... Most FIR filters have taps "before" and "after" (pre- and post-) the current signal ("cursor", like the cursor on a 'scope). That means they can change the signal before and after an impulse (assuming that is what you are looking at). That lets them "ring" before and after the impulse. IIR filters have no "pre" part; they mimic conventional analog filters in that regard, so any "ringing" only happens after the impulse.

Here's a simple FIR filter diagram; an IIR would look a little different and have no "pre-emphasis" tap. The delays allow the FIR filter to add signal before (PRE1, PRE2) and after (post, PST) the current (C0, main) time point.

Filter theory is an interesting subject but (well) beyond the scope of this thread.

HTH - Don

 

[dc655321]

I know but you can put a squarewave through such a filter and in that case the squarewave doesn't look like the familiar symmetric Gibbs effect.
Instead the parts of the 'ringing' where it is absent seems to have added to the other edge.

I know... this can be explained by math I don't understand but would like to see a 'simple' to understand explanation for the 'move' of the ' ringing'.

I guess you're replying to me?
I don't fully understand your description in the quoted section above.

"...put a squarewave through such a filter..."
You mean an IIR filter here, correct?

 

[solderdude]

Handwaving... Most FIR filters have taps "before" and "after" (pre- and post-) the current signal ("cursor", like the cursor on a 'scope). That means they can change the signal before and after an impulse (assuming that is what you are looking at). That lets them "ring" before and after the impulse. IIR filters have no "pre" part; they mimic conventional analog filters in that regard, so any "ringing" only happens after the impulse.

Here's a simple FIR filter diagram; an IIR would look a little different and have no "pre-emphasis" tap. The delays allow the FIR filter to add signal before (PRE1, PRE2) and after (post, PST) the current (C0, main) time point.

View attachment 142719

Filter theory is an interesting subject but (well) beyond the scope of this thread.

HTH - Don

Understood... but why is the 'ringing' of an IIR filter after the change bigger in amplitude and longer ?
Eyeballing the amplitudes it seems like the amplitude is double that of a FIR but spread before and after a change.

 

[danadam]

I know... this can be explained by math I don't understand but would like to see a 'simple' to understand explanation for the 'move' of the ' ringing'.

I don't know if it is correct but I always assumed that this is because IIR changes the phase of square wave's components. In your usual square wave all harmonics have the same phase (or different by n2π), but if you push them around in a right way, then I assume you can move the "ringing" to the other side.

 

[dc655321]

Understood... but why is the 'ringing' of an IIR filter after the change bigger in amplitude and longer ?
Eyeballing the amplitudes it seems like the amplitude is double that of a FIR but spread before and after a change.

Depends on filter properties of course, but that is one of the tradeoffs: no pre-ringing for IIR here because that is now added to the duration of the post-ringing.

EDIT: this may just muddy the waters

Spoiler: FIR linear and minimum phase LPF

import numpy as np
import scipy.signal as sig
import matplotlib.pyplot as plt


h_lin = sig.firwin2(255, [0, 0.25, 0.275, 1], [1, 1, 0, 0])
h_min = sig.minimum_phase(h_lin, method='homomorphic')

fig, axs = plt.subplots(3)
for h, style, color, label in zip((h_lin, h_min), ('-', '--'), ('k', 'r'), ('linear phase', 'min phase')):
    w, H = sig.freqz(h)
    w, gd = sig.group_delay((h, 1))
    w /= np.pi
    
    axs[0].plot(h, color=color, linestyle=style, label=label)
    axs[1].plot(w, 20*np.log10(np.abs(H)), color=color, linestyle=style, label=label)
    axs[2].plot(w, gd, color=color, linestyle=style, label=label)
    
handles, labels = plt.gca().get_legend_handles_labels()
fig.legend(handles, labels, loc='upper center')

 

[DonH56]

Understood... but why is the 'ringing' of an IIR filter after the change bigger in amplitude and longer ?
Eyeballing the amplitudes it seems like the amplitude is double that of a FIR but spread before and after a change.

I don't know what you mean by "after the change" but the signal properties are determined by the filter structure, including number of taps and how they are weighted, so can be all over the map. I have some other things in Life going on; perhaps it would be better to start a thread on filter theory. It is a big and popular subject and not at all related to this thread. I am less concerned about thread drift than about the info getting lost under the wrong title; selfishly, since I am usually the one wasting my time trying to find it when someone asks an hour or year from now.

 

[gene_stl]

Don how about some exposition on the rise time of square waves when used for audio testing (without FFTs and computers but with oscilloscopes )

I have seen some borderline stable amps blown up (a matched pair of SWTP Tigers from and in the late seventies) by feeding them fast rise square waves at too high a frequency. This can be dangerous for some amps. Square wave fed to audio equipment should be band limited and frequency limited.

 

[DonH56]

Don how about some exposition on the rise time of square waves when used for audio testing (without FFTs and computers but with oscilloscopes )

I have seen some borderline stable amps blown up (a matched pair of SWTP Tigers from and in the late seventies) by feeding them fast rise square waves at too high a frequency. This can be dangerous for some amps. Square wave fed to audio equipment should be band limited and frequency limited.

Not sure what you want me to say? Seems like you've had the same experience as many of us -- without proper input filtering, which IMO should be part of the amp, then high-slew signals can cause all sorts of problems. There were some early (and not so early) opamps that would totally freak out and invert their outputs when the input was slew limited by a large-signal input step. Guys like Scott Wurcer could (and did) write books about things like that...

I am a proponent of square-wave testing but agree with limiting the bandwidth to something at least quasi-reasonable. Since a number of phono cartridges would generate spikes to 100 kHz or more, I usually applied a 100 kHz filter or adjusted the rise/fall times of my pulse generator for such testing. Good distortion performance often requires bandwidth a decade or so above the target maximum frequency, at least internally, so 100 kHz seemed a reasonable value.

Note that fast waveforms, or rather waveforms with high frequency content, can be problematic for ADC/FFT-based analyzers too. Audio bandwidth inputs are also susceptible to slew limiting, ADC aliasing, and all that jazz.

SWTP Tigers were nice amps but had their quirks... Thermal runaway and stability among them IIRC. They were a fad when I was in HS/college and for a while I kept a drawer of output transistors for them. For them and Blaze Linears...

 

[solderdude]

I don't know if it is correct but I always assumed that this is because IIR changes the phase of square wave's components. In your usual square wave all harmonics have the same phase (or different by n2π), but if you push them around in a right way, then I assume you can move the "ringing" to the other side.

Yes, this makes perfect sense to me (along with the picture of @dc655321
minimum phase... linear phase..

 

[gene_stl]

The incident I saw was an audio engineer (a real EE) who should have known better blew up two tigers on the test bench. The big 60-75 watt ones (Universal Tiger??) I think he didn't like the guy who brought them in to his impromptu amplifier clinic. He did fix them for the guy but made him beg. I didn't actually like the guy either(he was DEFINITELY an audiophile ) but I had the distinct feeling that some of it had happened on purpose. The deed was done with square waves.

 

[RayDunzl]

Long ago, I was surprised to see how many odd harmonics an analyzer could pick out from the output of the preamp on the way to the speakers...

With a 10Hz square input, I think it got to about the 1,150th odd harmonic in the series, before band-limit of the DAC was hit.

Click the image to expand...

https://www.audiosciencereview.com/forum/index.php?threads/an-unexpected-measurement.628/#post-18931

 

[restorer-john]

A quick glance at the amplifier schematic can identify the input filtering and the corner frequency/ies along with poles in the NFB loop/s.

But we can use a really fast square to throw at the amplifier (small signal 2.83V) and see a) whether it's stable and b) it's approx upper -3dB point (Fc = 0.35 / T10-90%).

 

[restorer-john]

For them and Blaze Linears...

Or Flame Linears.

The were TV horizontal output transistors weren't they? It's been a while.

 

[DonH56]

Or Flame Linears.

The were TV horizontal output transistors weren't they? It's been a while.

I think so but am not sure. As you say, been a while... They had to be tightly matched and were hard to find near the end.