- Joined
- May 1, 2021
- Messages
- 469
- Likes
- 1,424
- Introduction –
The effect of a polarity flip is described in many blog posts and videos as being ‘different’ from a phase shift, with the main argument being that “since a phase shift is equivalent to a time delay, it cannot equate a polarity flip”, or something to that effect. We will show that a polarity flip can indeed be described via a particular phase, namely 180 degrees across all frequencies, and that this should not be confused with a time delay.
- Details –
All necessary details are included in the attached sheet (Polarity.pdf: “Overview of Phase, Polarity, and Delay Aspects of Real and Causal All-Pass Systems”), but if you are not too familiar with such concepts as ‘negative frequencies’, and ‘Hermitian symmetry’, perhaps the following explanation can shed some light on the topic.
The entirety of this debate can be summed up in what is often called ‘The most beautiful equation in the world’, namely Euler’s identity:
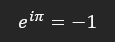
What is says is that the numbers e, i, and pi, (two being transcendental numbers, and one being imaginary), can be combined in way that gives us the rather mundane result of minus one. For our purpose here, we can note that a polarity inversion can be described via a sign inversion i.e., the right side of the equation, and so if we can relate the left-side expression to a phase shift, then we are done.
Via the concept of phasors, we can describe signals and system in a complex (real and imaginary parts) notation. If a signal has an amplitude A and a phase angle phi as function of angular frequency omega, it can be written in exponential form as
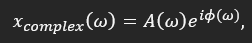
with a corresponding real and time-dependent the signal

which is what we would measure. The phasor amplitude and phase are what we see when we plot signal and system frequency responses (the amplitude response and the phase response) both as function of frequency.
By comparing equations, we can see that the phasor phase phi is exactly pi for a sign change, and that this holds for all frequencies. As time passes, the total phase does indeed change, but the initial phasor phase remains(!). This is probably the reason that the blog posts confuse phase and time to argue that a phase shift cannot describe a polarity inversion. We can certainly introduce a signal with one phasor phase and a time delay added, and make it look like another signal with no time delay and a different phasor phase, but only when viewed steady-state or non-causally (again, see the sheet). But this does not mean that the signals ARE inherently the same.
The only things left is to realize that pi in radians is the same as 180 degrees, and that there is some ambiguity when it comes to phase, so that -180 and +180 degrees are the same, and that we cannot for one phase at one frequency see how many turns the phasor took to get to that phase value; the sheet shows more details on this. If this does not feel comfortable, just remember that for real numbers there is also an ambiguity in a sign change on its own, as we cannot differentiate between multiplying by -1 once, thrice, five times, and so on. We typically plot the -180 degrees version of this sign change operation/polarity inversion, since we anyway often plot in this lower right quadrant for more typical filters that tend downwards as a function of frequency when causal.
While there are temporal characteristics related to the phasor phase, we should not consider describing the polarity inversion via delays. Interchanging two wires does not add a delay and calculating the group delay before and after the polarity inversion will both give the same result (namely zero), as seen from the attached sheet. In fact, looking at the phase value at only one frequency is not enough to state anything about the delay aspects of a signal or system; you need to know more phase values so that the gradient can be calculated.
- Conclusion –
While many blog posts argue otherwise, a polarity inversion is exactly described via a phase shift of 180 degrees. The phase in question is the phasor phase, which should not be confused with the apparent phase shift resulting from a delay. There is nothing in the textbooks on signal processing that suggests that a sign inversion should be tied to a time delay in any way, so this is a topic that has been polluted by incorrect assumptions. A good aspect of these blog posts is that they are mostly well written, and it is very clear where people take a wrong turn. Being external examiner on a lot of BSc and MSc projects, I much prefer good reports where the analysis is incorrect but well described, over reports that seemingly arrive at correct results but with an unclear analysis. People seem very split and emotional about this very topic, and it will be interesting to see what you all think of it. From a signal-processing point of view, this seems like a moot point; but with the attached sheet I believe that all necessary aspects are covered to not only arrive at the conclusion, but also illustrate why there is this confusion.
- About me -
René Christensen, BSEE, MSc (Physics), PhD (Microacoustics), FEM and BEM simulations specialist in/for loudspeaker, hearing aid, and consultancy companies. Own company Acculution, blog at acculution.com/blog
The effect of a polarity flip is described in many blog posts and videos as being ‘different’ from a phase shift, with the main argument being that “since a phase shift is equivalent to a time delay, it cannot equate a polarity flip”, or something to that effect. We will show that a polarity flip can indeed be described via a particular phase, namely 180 degrees across all frequencies, and that this should not be confused with a time delay.
- Details –
All necessary details are included in the attached sheet (Polarity.pdf: “Overview of Phase, Polarity, and Delay Aspects of Real and Causal All-Pass Systems”), but if you are not too familiar with such concepts as ‘negative frequencies’, and ‘Hermitian symmetry’, perhaps the following explanation can shed some light on the topic.
The entirety of this debate can be summed up in what is often called ‘The most beautiful equation in the world’, namely Euler’s identity:
What is says is that the numbers e, i, and pi, (two being transcendental numbers, and one being imaginary), can be combined in way that gives us the rather mundane result of minus one. For our purpose here, we can note that a polarity inversion can be described via a sign inversion i.e., the right side of the equation, and so if we can relate the left-side expression to a phase shift, then we are done.
Via the concept of phasors, we can describe signals and system in a complex (real and imaginary parts) notation. If a signal has an amplitude A and a phase angle phi as function of angular frequency omega, it can be written in exponential form as
with a corresponding real and time-dependent the signal
which is what we would measure. The phasor amplitude and phase are what we see when we plot signal and system frequency responses (the amplitude response and the phase response) both as function of frequency.
By comparing equations, we can see that the phasor phase phi is exactly pi for a sign change, and that this holds for all frequencies. As time passes, the total phase does indeed change, but the initial phasor phase remains(!). This is probably the reason that the blog posts confuse phase and time to argue that a phase shift cannot describe a polarity inversion. We can certainly introduce a signal with one phasor phase and a time delay added, and make it look like another signal with no time delay and a different phasor phase, but only when viewed steady-state or non-causally (again, see the sheet). But this does not mean that the signals ARE inherently the same.
The only things left is to realize that pi in radians is the same as 180 degrees, and that there is some ambiguity when it comes to phase, so that -180 and +180 degrees are the same, and that we cannot for one phase at one frequency see how many turns the phasor took to get to that phase value; the sheet shows more details on this. If this does not feel comfortable, just remember that for real numbers there is also an ambiguity in a sign change on its own, as we cannot differentiate between multiplying by -1 once, thrice, five times, and so on. We typically plot the -180 degrees version of this sign change operation/polarity inversion, since we anyway often plot in this lower right quadrant for more typical filters that tend downwards as a function of frequency when causal.
While there are temporal characteristics related to the phasor phase, we should not consider describing the polarity inversion via delays. Interchanging two wires does not add a delay and calculating the group delay before and after the polarity inversion will both give the same result (namely zero), as seen from the attached sheet. In fact, looking at the phase value at only one frequency is not enough to state anything about the delay aspects of a signal or system; you need to know more phase values so that the gradient can be calculated.
- Conclusion –
While many blog posts argue otherwise, a polarity inversion is exactly described via a phase shift of 180 degrees. The phase in question is the phasor phase, which should not be confused with the apparent phase shift resulting from a delay. There is nothing in the textbooks on signal processing that suggests that a sign inversion should be tied to a time delay in any way, so this is a topic that has been polluted by incorrect assumptions. A good aspect of these blog posts is that they are mostly well written, and it is very clear where people take a wrong turn. Being external examiner on a lot of BSc and MSc projects, I much prefer good reports where the analysis is incorrect but well described, over reports that seemingly arrive at correct results but with an unclear analysis. People seem very split and emotional about this very topic, and it will be interesting to see what you all think of it. From a signal-processing point of view, this seems like a moot point; but with the attached sheet I believe that all necessary aspects are covered to not only arrive at the conclusion, but also illustrate why there is this confusion.
- About me -
René Christensen, BSEE, MSc (Physics), PhD (Microacoustics), FEM and BEM simulations specialist in/for loudspeaker, hearing aid, and consultancy companies. Own company Acculution, blog at acculution.com/blog


