I should have stopped a while ago, but I appear to lack self controlYes, thank you. I had been reflexively using rfft (assumes purely Real, Hermitian).
This is all starting to dredge up memories of time/phase shift and frequency shift/modulation properties of Fourier transforms.
Should probably stop before we have to get into quadrature sampling and how 2*bandwidth is not always necessary
-
WANTED: Happy members who like to discuss audio and other topics related to our interest. Desire to learn and share knowledge of science required. There are many reviews of audio hardware and expert members to help answer your questions. Click here to have your audio equipment measured for free!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Analytical Analysis - Polarity vs Phase
- Thread starter René - Acculution.com
- Start date
TLDR: Sorry everyone, @René - Acculution.com, @dc655321, I'm completely wrong on all counts.
I was missing the factor of signum(omega) when applying the phase shift in the frequency domain. Phase shift of phi radians in the frequency domain is e^(j * signum(omega) * phi) * F{x(t)} which is clearly not the same as e^(j * phi) * x(t) as some of my prior posts asserted, and produces the expected phase shift for real signals.
Furthermore, this corrected operation, when applied to a real signal, does preserve Hermitian symmetry, @dc655321 your original code was correct.
Just for the record, I've fixed and attached the script I posted in #35 which now gets the correct result:
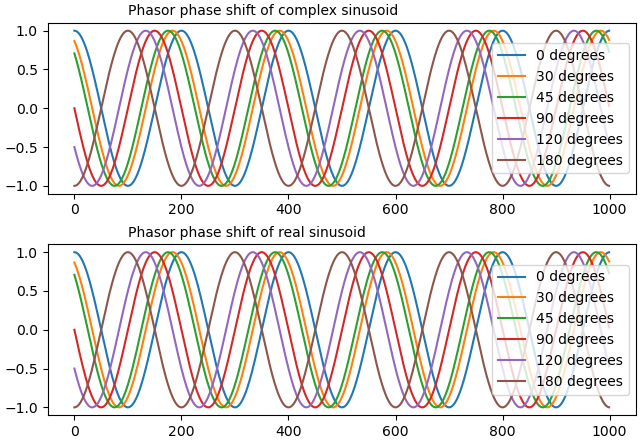
I was missing the factor of signum(omega) when applying the phase shift in the frequency domain. Phase shift of phi radians in the frequency domain is e^(j * signum(omega) * phi) * F{x(t)} which is clearly not the same as e^(j * phi) * x(t) as some of my prior posts asserted, and produces the expected phase shift for real signals.
Furthermore, this corrected operation, when applied to a real signal, does preserve Hermitian symmetry, @dc655321 your original code was correct.
Just for the record, I've fixed and attached the script I posted in #35 which now gets the correct result:
Attachments
Last edited:
Nice sheet and thread! One question. The H function it's defined as ℂ^1000 → ℂ^2000 in some place. Where those numbers come from?
P.D. I imagine you all use degrees instead of pi multiples to avoid having to print the letter pi in the phase inversion selector in sub-woofers, right?
P.D. I imagine you all use degrees instead of pi multiples to avoid having to print the letter pi in the phase inversion selector in sub-woofers, right?
Those aren't powers, they're the axis labels from the plot directly above that line.Nice sheet and thread! One question. The H function it's defined as ℂ^1000 → ℂ^2000 in some place. Where those numbers come from?
Those aren't powers, they're the axis labels from the plot directly above that line.
 xDDDDD
xDDDDD- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,302
- Thread Starter
- #46
Thanks for the clarification and your contributions, and 'on all counts' is certainly not true ;-)TLDR: Sorry everyone, @René - Acculution.com, @dc655321, I'm completely wrong on all counts.
I was missing the factor of signum(omega) when applying the phase shift in the frequency domain. Phase shift of phi radians in the frequency domain is e^(j * signum(omega) * phi) * F{x(t)} which is clearly not the same as e^(j * phi) * x(t) as some of my prior posts asserted, and produces the expected phase shift for real signals.
Furthermore, this corrected operation, when applied to a real signal, does preserve Hermitian symmetry, @dc655321 your original code was correct.
Just for the record, I've fixed and attached the script I posted in #35 which now gets the correct result:
View attachment 177914
For those who might just be inspired to read more about phasors and signal processing in general, here are some recommended references:
"Communication Systems", A.B. Carlson, McGrawHill
"Introduction to Electric Circuits", D. Svoboda, Wiley
"Signals and Systems", Oppenheim et al., Pearson
"The Scientist and Engineer's Guide to Digital Signal Processing", S.W. Smith, Smith/CTP
"Discrete-Time signal Processing", Oppenheim & Schafer, Prentice Hall
"Understanding Digital Signal Processing", R.G. Lyons, PH PTR
"Advanced Engineering Mathematics" E. Kreyszig, Wiley
/René
Some other resources I found searching were I usually learn things (by Oppenheim himself):
https://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/
https://www.edx.org/course/discrete...D=97e5bc9ef1693271a3711d36c8dab434&position=1
I haven't taken any audio or electronics course (yet) on edx, but I've taken many others and I can't recommend enough the courses from MITx for their quality and great pedagogical value.
https://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/
https://www.edx.org/course/discrete...D=97e5bc9ef1693271a3711d36c8dab434&position=1
I haven't taken any audio or electronics course (yet) on edx, but I've taken many others and I can't recommend enough the courses from MITx for their quality and great pedagogical value.
@René - Acculution.com I just finished the video.
Kudos… You did a very good job on that!
One thing that generally bugs me about speaker tests is that there is rarely shown a step response.
I think I can fix FR with a DSP, but I don’t think that I fix a bad step response with bi-quads.
So I would always prefer to see a step response and an impulse response over just the FR.
Should I assume that the Impulse response is essentially analogous to H(s) ?
(A pure Dirac delta function is a time domain description of H(s), so I guess H(s) is more of the FR description of the system???)
And then amps and DSP everything is tones, or 19k+20k multi tones, or more multi tones.
Are square waves or other signals better for describing and evaluating electronics?
I guess it is apparent that I am somewhat in the temporal camp.
Kudos… You did a very good job on that!
One thing that generally bugs me about speaker tests is that there is rarely shown a step response.
I think I can fix FR with a DSP, but I don’t think that I fix a bad step response with bi-quads.
So I would always prefer to see a step response and an impulse response over just the FR.
Should I assume that the Impulse response is essentially analogous to H(s) ?
(A pure Dirac delta function is a time domain description of H(s), so I guess H(s) is more of the FR description of the system???)
And then amps and DSP everything is tones, or 19k+20k multi tones, or more multi tones.
Are square waves or other signals better for describing and evaluating electronics?
I guess it is apparent that I am somewhat in the temporal camp.
- Introduction –
The effect of a polarity flip is described in many blog posts and videos as being ‘different’ from a phase shift, with the main argument being that “since a phase shift is equivalent to a time delay, it cannot equate a polarity flip”, or something to that effect. We will show that a polarity flip can indeed be described via a particular phase, namely 180 degrees across all frequencies, and that this should not be confused with a time delay.
…
I always think of the 180 degrees phase shift in the time domain.
So each phasor, at each point in time, gets rotated 180 degrees.
But I have not considered it in the frequency domain.
And I usually do not think about signals going from -inf to +inf in time, if I can think of a Direc delta function going from 0 to 1 when quickly passes by me in time.
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,302
- Thread Starter
- #51
Hi Holmz. Well, phase is really a frequency domain variable, and even more specifically a steady-state frequency variable. But yes, the rotation over time is overlaid by whatever rotation the inherent phase of the system introduces itself. If that makes sense... For steady state signals, one is by default considering infinite time, and this is where a lot of the confusion comes from, as looking at steady state only (and one frequency only), a time-delay will look the same as a polarity flip, but the transient behavior will be different. These aspects are what make the video so long ;-)I always think of the 180 degrees phase shift in the time domain.
So each phasor, at each point in time, gets rotated 180 degrees.
But I have not considered it in the frequency domain.
And I usually do not think about signals going from -inf to +inf in time, if I can think of a Direc delta function going from 0 to 1 when quickly passes by me in time.
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,302
- Thread Starter
- #52
I agree, I would at least like to see the step response; without any comments is fine. It does give some insights, which may or may not be deemed relevant. I would also like to have THE PHASE OF THE PRESSURE, please!@René - Acculution.com I just finished the video.
Kudos… You did a very good job on that!
One thing that generally bugs me about speaker tests is that there is rarely shown a step response.
I think I can fix FR with a DSP, but I don’t think that I fix a bad step response with bi-quads.
So I would always prefer to see a step response and an impulse response over just the FR.
Should I assume that the Impulse response is essentially analogous to H(s) ?
(A pure Dirac delta function is a time domain description of H(s), so I guess H(s) is more of the FR description of the system???)
And then amps and DSP everything is tones, or 19k+20k multi tones, or more multi tones.
Are square waves or other signals better for describing and evaluating electronics?
I guess it is apparent that I am somewhat in the temporal camp.
Yes, the impulse response and the transfer function are each others analog in the time domain and the frequency domain, respectively. So Laplace transform the impulse response and you will get the transform function. An impulse will be a distinct line in the time domain, and a flat reponse in the frequency domain (so all frequencies are excited equally), and so all the necessary (linear) information about the system will be known when knowing how it responds to an impulse.
I don't really know much about the practicalities of testing electronics, sorry, but the response to a square signal will certain reveal some of the temporal behavior (rise-time, phase shift).
And thanks for your kind words.
I agree, I would at least like to see the step response; without any comments is fine. It does give some insights, which may or may not be deemed relevant.
…
@amirm ^step response please^
… I would also like to have THE PHASE OF THE PRESSURE, please!It is often omitted in measurements, or only the phase of the impedance is shown, which is nice, but not enough.
…
Like the polarity to see if the step is negative rather than positive?
Isn’t the step response more like a minimum phase condition for the speaker?
I am not sure I am computing… as it starts at 0 and goes to say unity.
Then the step measurement either jumps up, or down, and either decays, or wriggles.
So in the time domain at least, there is not a lot of phase info.
…
Yes, the impulse response and the transfer function are each others analog in the time domain and the frequency domain, respectively. So Laplace transform the impulse response and you will get the transform function. An impulse will be a distinct line in the time domain, and a flat reponse in the frequency domain (so all frequencies are excited equally), and so all the necessary (linear) information about the system will be known when knowing how it responds to an impulse.
Tak!
I got it.
…
And thanks for your kind words.
I am not known for kindness.
You earned the words.
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,302
- Thread Starter
- #54
Amir already shows step response, I think@amirm ^step response please^
Like the polarity to see if the step is negative rather than positive?
Isn’t the step response more like a minimum phase condition for the speaker?
I am not sure I am computing… as it starts at 0 and goes to say unity.
Then the step measurement either jumps up, or down, and either decays, or wriggles.
So in the time domain at least, there is not a lot of phase info.
Tak!
I got it.
I am not known for kindness.
You earned the words.
Just as the impedance has a magnitude and a phase, so does the pressure. The pressure is represented as one complex amplitude per frequency; the so-called phasor. The magnitude is shown in dB, but the phase is often not shown. So you don't have the full picture. Imagine runners at the starting line. Each have their right foot in front, and left back. We define this as zero phase. Each runner represents a frequency, and so across the frequency range we have initial phasors being zero phase at all frequencies. A polarity flip means that they all put left foot front, right foot back. No one is running yet, there is no time delay involved. In general though, each of them can have their own phasor phase, or initial phase, with some arbitrary foot placement. This is the general phase.
A pure polarity flip, flips everything upside down in the time domain. Step response, whatever. But it is difficult to say that a system inherently 'has' a polarity. It has a phase, and a polarity flip will add/subtract 180 deg to the phasor phases across the entire frequency range in the frequency domain.
Last edited:
Got it @René - Acculution.com - in Freq on the X-axis and not time on the X-axis.
- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,302
- Thread Starter
- #56
Yep. Phase across the frequency axis. This along with magnitude will give the complete transfer function. The steady state behavior is seen directly from the plot, and transient behavior can be calculated separately as long as the steady state transfer function is known, via Inverse Laplace transformations.Got it @René - Acculution.com - in Freq on the X-axis and not time on the X-axis.
Similar threads
- Replies
- 17
- Views
- 6K
- Replies
- 12
- Views
- 2K
- Replies
- 46
- Views
- 4K
- Replies
- 4
- Views
- 624
