Ok, that old BS about "only one sample time resolution" came up again elsewhere. I made the following demonstration to put the screws to that.
I generated a 10kHz sine wave at 44.1 kHz sampling rate. The matlab file is attached. I generated 128 discrete phases uniformly split over one cycle, so each new phase shift is equal to 4.41/128 sample delay, or about .7 microseconds. The routine plots the first 8, making the very obvious point that they are different. Q. (obscenity) E. D.
Note, I had to add a .txt to the filename to get ASR to load it, apparently we don't like .m files. If you want to run it under matlab or octave, you'll have to strip the .txt from the end.
the resulting plot:
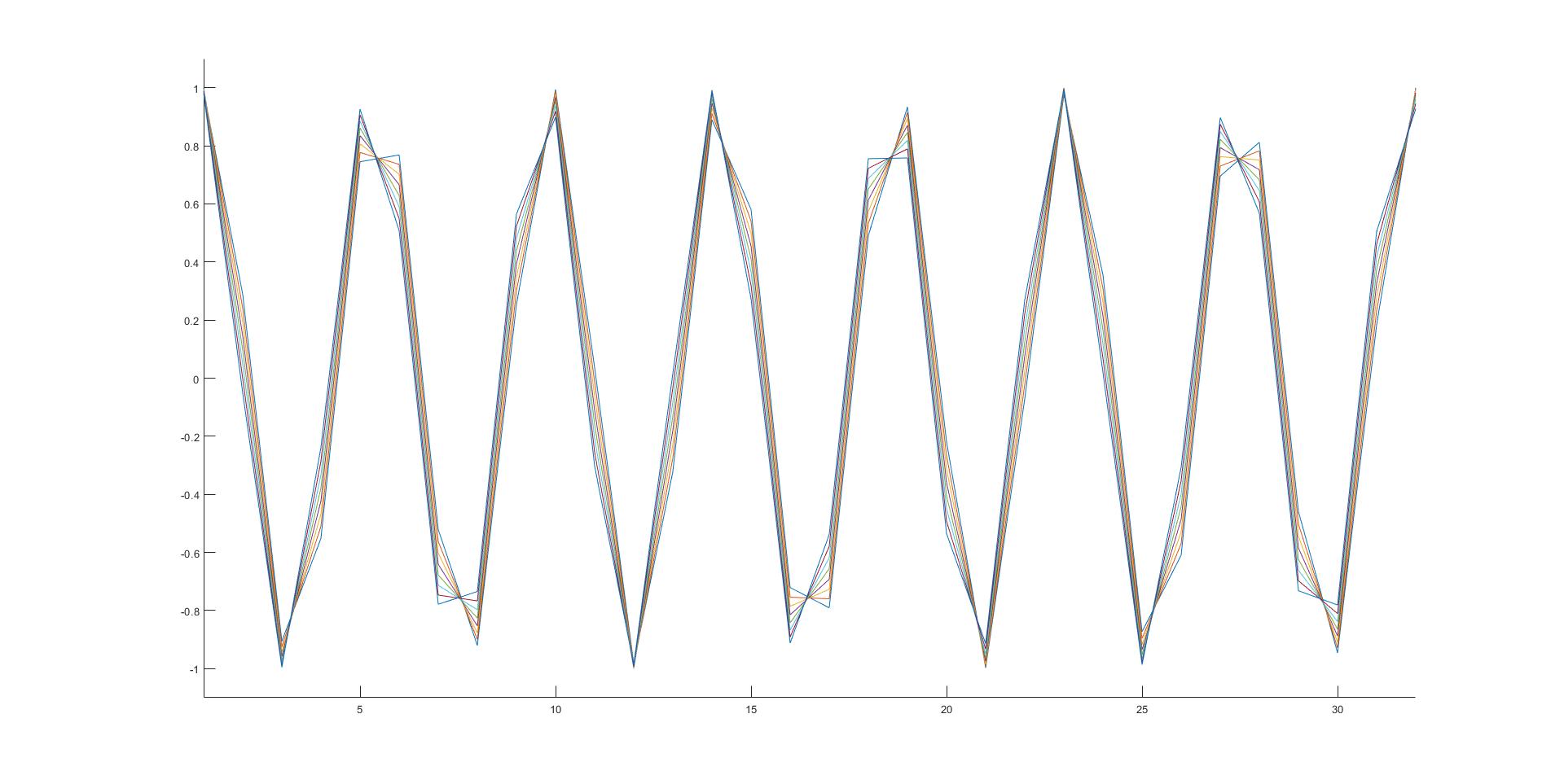
I generated a 10kHz sine wave at 44.1 kHz sampling rate. The matlab file is attached. I generated 128 discrete phases uniformly split over one cycle, so each new phase shift is equal to 4.41/128 sample delay, or about .7 microseconds. The routine plots the first 8, making the very obvious point that they are different. Q. (obscenity) E. D.
Note, I had to add a .txt to the filename to get ASR to load it, apparently we don't like .m files. If you want to run it under matlab or octave, you'll have to strip the .txt from the end.
the resulting plot:
