Your breathing was too loud, very distracting!
-
WANTED: Happy members who like to discuss audio and other topics related to our interest. Desire to learn and share knowledge of science required. There are many reviews of audio hardware and expert members to help answer your questions. Click here to have your audio equipment measured for free!
Springs Under My Speakers: What's Happening?
- Thread starter MattHooper
- Start date
Ha, don't know what that sound comes from, but probably not my breathing.
I have an ACH-01 accelerator and amp that I would like to test in this respect but time has not been there
When it comes to audio quality around these things I believe the time domain is where we'll see some interesting stuff. Like energy storage.
Linkwitz wrote about that here;
http://linkwitzlab.com/frontiers_2.htm#M
Linkwitz wrote about that here;
http://linkwitzlab.com/frontiers_2.htm#M
And just one comment regarding the esoteric solutions (GAIA etc). Although they may work as intended, simply cutting adequate sizes of soft mouse or sleeping pads are most likely sufficient for isolation.
restorer-john
Grand Contributor
That's a Pioneer 1980s turntable footer, from the stable hanging platter series. (Inverted bearing). That "sheath" is not original, neither is the grommet.
I have a lot of those in my spares box...
Used on the PL-xxxD series right up to the PLL-1000/a.
- Joined
- Jan 15, 2020
- Messages
- 7,111
- Likes
- 17,959
To understand the complex thematic a loudspeaker on the floor can be minimally modelled as a mass-spring-damper 2 body system if we reduce the motions to one direction
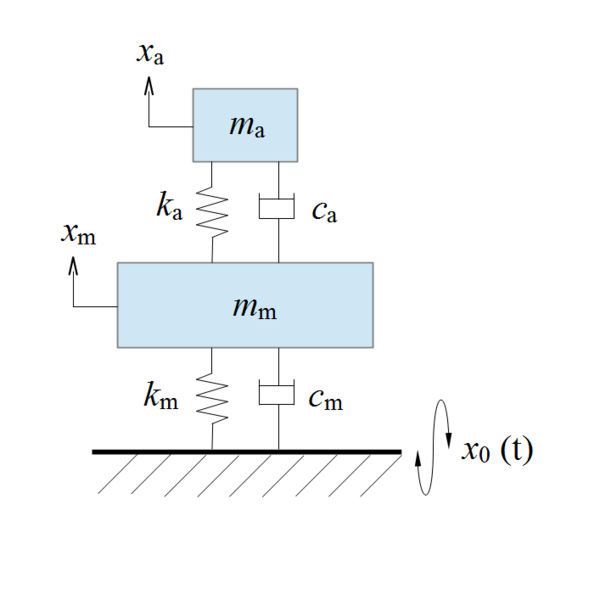
where the complete loudspeaker (enclosure plus drivers) is mass ma, the floor is mass mm and the floor has its own stiffness km and damping and cm in relation to the earth with its "infinite" mass. The relative movement between loudspeaker and floor is coupled through the stiffness ka and damping ca of the connection between them (for example loudspeaker base or feet).
Excitation in this case been modelled as a sinusoidal force at the loudspeaker mass ma and the vertical direction of xa through the inertial reaction to the loudspeakers membranes motion (in this simplified teaching case of course also oscillating in vertical direction).
Ideally for our purposes we want the oscillation amplitude of both the loudspeaker mass xa and floor mass xm to be minimised, even more for higher frequencies as with increasing frequency the same amplitude creates a higher sound pressure.
Ideally our floor has very high stiffness and damping and thus isn't prone to high excitation, in this case we want as high stiffness ka as possible for the loudspeaker to floor connection, which for the extreme case can be thought as just one combined mass and will minimise the loudspeaker oscillation amplitude too. Using in this case feet with high compliance (= low stiffness) is counterproductive as it will allow unnecessarily higher oscillations of the total loudspeaker (enclosure), especially till the resonance frequency of the coupling stiffness with the mass is reached, ω0 = sqrt (ka/ma):
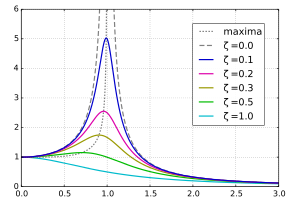
In above plot x axis is the normalised excitation frequency ω/ω0 and y axis is the normalised oscillation amplitude for different normalised damping factors ζ, as it can be seen above 1 (ω/ω0>1) the oscillation amplitude gets reduced but before its higher, especially close to the resonance frequency 1.0 (ω/ω0=1).
This result can be used also in the case our floor stiffness is not optimally high enough. In this case the first step is to reduce the loudspeaker oscillation itself as much as possible by increasing its mass, for example with heavy stone plates directly and stiffly connected to the loudspeakers base. Then we could ideally choose the stiffness and damping of the connection of the plate to the floor by appropriate elastomers and/or mechanical spring/viscous dampers, we want a low enough stiffness that brings the resonance frequency of the coupling lower than the lowest frequency we will excite (for example lower than 20 Hz) and damping factor as high as possible, mind you that damping factor is often a compromise with low stiffness.
As it can be seen even for this significantly simplified case the problem is quite complex and in reality it gets more complex as we have (partially even coupled) vibrations in all 3 directions and not ideally stiff subsystems which show even their own (theoretically infinite) eigenmodes, so its obvious that generic solutions like "audiophile feet" offered cannot be a guarantee for success. To sum it up our the solution can be very different depending on individual parameters like the stiffness of the floor.
where the complete loudspeaker (enclosure plus drivers) is mass ma, the floor is mass mm and the floor has its own stiffness km and damping and cm in relation to the earth with its "infinite" mass. The relative movement between loudspeaker and floor is coupled through the stiffness ka and damping ca of the connection between them (for example loudspeaker base or feet).
Excitation in this case been modelled as a sinusoidal force at the loudspeaker mass ma and the vertical direction of xa through the inertial reaction to the loudspeakers membranes motion (in this simplified teaching case of course also oscillating in vertical direction).
Ideally for our purposes we want the oscillation amplitude of both the loudspeaker mass xa and floor mass xm to be minimised, even more for higher frequencies as with increasing frequency the same amplitude creates a higher sound pressure.
Ideally our floor has very high stiffness and damping and thus isn't prone to high excitation, in this case we want as high stiffness ka as possible for the loudspeaker to floor connection, which for the extreme case can be thought as just one combined mass and will minimise the loudspeaker oscillation amplitude too. Using in this case feet with high compliance (= low stiffness) is counterproductive as it will allow unnecessarily higher oscillations of the total loudspeaker (enclosure), especially till the resonance frequency of the coupling stiffness with the mass is reached, ω0 = sqrt (ka/ma):
In above plot x axis is the normalised excitation frequency ω/ω0 and y axis is the normalised oscillation amplitude for different normalised damping factors ζ, as it can be seen above 1 (ω/ω0>1) the oscillation amplitude gets reduced but before its higher, especially close to the resonance frequency 1.0 (ω/ω0=1).
This result can be used also in the case our floor stiffness is not optimally high enough. In this case the first step is to reduce the loudspeaker oscillation itself as much as possible by increasing its mass, for example with heavy stone plates directly and stiffly connected to the loudspeakers base. Then we could ideally choose the stiffness and damping of the connection of the plate to the floor by appropriate elastomers and/or mechanical spring/viscous dampers, we want a low enough stiffness that brings the resonance frequency of the coupling lower than the lowest frequency we will excite (for example lower than 20 Hz) and damping factor as high as possible, mind you that damping factor is often a compromise with low stiffness.
As it can be seen even for this significantly simplified case the problem is quite complex and in reality it gets more complex as we have (partially even coupled) vibrations in all 3 directions and not ideally stiff subsystems which show even their own (theoretically infinite) eigenmodes, so its obvious that generic solutions like "audiophile feet" offered cannot be a guarantee for success. To sum it up our the solution can be very different depending on individual parameters like the stiffness of the floor.
Last edited:
Even though the results will differ depending on the floor type, a low resonant frequency will ensure that excitation is not occurring in the audible spectrum.
- Joined
- Jan 15, 2020
- Messages
- 7,111
- Likes
- 17,959
Yes I know. What I mean is that even though a soft foot can not be guaranteed to have an audible or measurable effect, they can at least guarantee for most cases that you don't get a problem.
No surprise at all.
Spikes couple the speaker to the floor so, depending on the floor type, spiking the speakers to it is just like adding a huge area cabinet vibration to the sound.
Using polymer type footers only absorbs vibration at relatively high frequencies so couples the cabinet vibration to the floor at low frequencies as well.
Springs of the correct stiffness will decouple the speaker from the floor giving a similar increase in quality to a well engineered cabinet over a crappy one but probably bigger (coupled floor area being bigger than cabinet area).
It is basic noise and vibration stuff I used to do research in 45 years ago.
As a rule of thumb for the isolation to be effective over the whole frequency range the isolating springs will deflect around 1" due to the weight of the mass being decoupled. The smaller the deflection the higher the frequency above which isolation will be taking place.
About the same as setting suspension pre-load.
For the same reasonAbout the same as setting suspension pre-load.
YepFor the same reason
Thanks for this. You mentioned there that problems might show up as distortion in frequency response measurements. So then would you say if REW shows distortion to be below the noise floor then don't worry about all this? Conversely, is there reason to question distortion measurements in the speaker reviews here where mounting isn't given a world of attention?
I'm not meaning to be disagreeable so much as to ask how any problems might be measured in a meaningful way that gets at what is actually heard.
deprogrammed
Active Member
I needed to raise my monitor tweeters up to ear height and was looking for something that would stop the desk from vibrating.
Yoga blocks, solved both issues.
Not sure about audibility....
The problem here is AFAIK there is no way to separate the sound being radiated by the drivers from that being radiated by the cabinet, or any mounting, by acoustic measurement.
It can be done by FE analysis though but no way Amir, or any of the rest of us, would be able to do that.
This is the sort of thing done at the design stage by the manufacturer in the high tech brands but, probably, not at all with the smaller makers.
mhardy6647
Grand Contributor
- Joined
- Dec 12, 2019
- Messages
- 12,885
- Likes
- 28,616
springs and speakers... I can only think of...
source: https://worldradiohistory.com/Archive-Catalogs/Lafayette-Catalogs/Lafayette-1965-650.pdf
The Fisher SpaceXpander!
sorry!
source: https://worldradiohistory.com/Archive-Catalogs/Lafayette-Catalogs/Lafayette-1965-650.pdf
The Fisher SpaceXpander!
sorry!
OP
MattHooper
Master Contributor
- Joined
- Jan 27, 2019
- Messages
- 8,809
- Likes
- 14,524
- Thread Starter
- #60
Wow, that's a lot of great replies!
I was probably most surprised by the apparent change in high frequencies and sense of resolution, they way things just cleared up. I've been playing tracks that I've heard a gazillion times on the Thiels - my "test" tracks especially - and it feels like looking through a microscope that has been focused. A sort of 'limitless resolution' impression where reverb trails go on "forever" and even in complex passages everything is so effortless to make out. But, if there is a reduction in distortion the effect on higher frequences makes some sense to me, given the relatively teeny excursions involved in a speaker's high frequencies. Presumably any distortion added by the speaker vibrating/floor vibrating would be "larger" and impactful relative to the excursions of, say, a tweeter vs the woofer. (Open to being corrected there, of course).
I was probably most surprised by the apparent change in high frequencies and sense of resolution, they way things just cleared up. I've been playing tracks that I've heard a gazillion times on the Thiels - my "test" tracks especially - and it feels like looking through a microscope that has been focused. A sort of 'limitless resolution' impression where reverb trails go on "forever" and even in complex passages everything is so effortless to make out. But, if there is a reduction in distortion the effect on higher frequences makes some sense to me, given the relatively teeny excursions involved in a speaker's high frequencies. Presumably any distortion added by the speaker vibrating/floor vibrating would be "larger" and impactful relative to the excursions of, say, a tweeter vs the woofer. (Open to being corrected there, of course).
Similar threads
