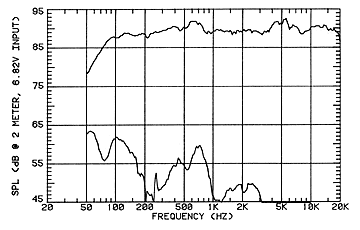
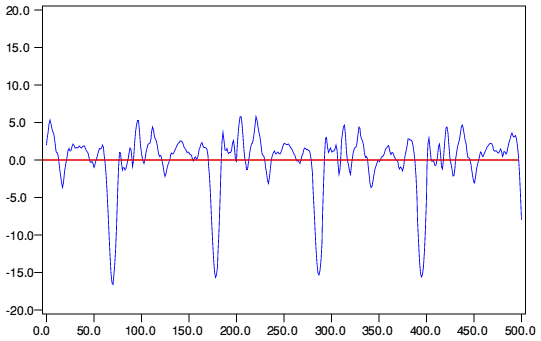
I'm interested in this. Loudspeakers probably add more distortion to the reproduced sound than everything else in the chain, but it's rarely talked about. I have a gut feeling that the infamous subjectivist claim that some systems "measure well but sound bad" may partly be about speakers that are equalized in order to have a flat frequency response, but which nevertheless have much distortion (it might even be that equalizing the drivers beyond their comfort zone creates distortion). So:
What do we know about it? What are the causes?
Why do most loudspeakers manufacturers avoid mentioning the issue when talking about their products?
Why is this almost never measured or quantified in reviews, even among us objectivist folks?
And: HOW does one measure this in a good way?
Would love to get some input on this...
What do we know about it? What are the causes?
Why do most loudspeakers manufacturers avoid mentioning the issue when talking about their products?
Why is this almost never measured or quantified in reviews, even among us objectivist folks?
And: HOW does one measure this in a good way?
Would love to get some input on this...