Upsampling - integer vs non-integer ratios - original samples

[ZolaIII]

IEEE 754 - Wikipedia

en.m.wikipedia.org

FP calculations are used by DSP's, SIMD's... and go up to 256 bit's while 32 bit is considered as full precision. You can find conversion rules there.

 

[mansr]

You don't need an ideal one, any windowed sinc preserve input samples.
This property is particularly important for half band filter ( for x2 upsampler) : you only need to compute half of the output samples, the other half are just the input samples.

Yes, you are right; I didn't think it through properly. Any (FIR) filter where every Nth coefficient is zero will indeed preserve the input samples when used as an interpolation filter for upsampling by a factor N. The attenuation below the cut-off frequency is exactly matched by the imaging above.

 

[mansr]

Regarding preserving input samples, the important lesson is that this is itself not an advantage, unless for some reason you need the process to be exactly reversible. Although the samples are preserved with some filters, the frequencies are not. In many cases, the end goal is better served by allowing the samples to be altered.

 

[Music1969]

You don't need an ideal one, any windowed sinc preserve input samples.

You just made Rob Watts spit out his afternoon cup of tea

Hugo TT 2 by Chord Electronics - The Official Thread

I understand this sentiment completely. If it wasn't for Covid lockdown still in my area I would probably revert to my DAP, iem and a few good tunes. I can totally relate to that! Mine is covered with dust:gs1000smile:.

www.head-fi.org

 

[mansr]

You just made Rob Watts spit out his afternoon cup of tea

Hugo TT 2 by Chord Electronics - The Official Thread

I understand this sentiment completely. If it wasn't for Covid lockdown still in my area I would probably revert to my DAP, iem and a few good tunes. I can totally relate to that! Mine is covered with dust:gs1000smile:.

www.head-fi.org

In case there was any doubt, nothing in that post makes any sense.

 

[mansr]

So Rob Watts keeps waffling on about how a windowed sinc filter is inferior to a "true" sinc. By this he means, I believe, that all the filter coefficients should match the values of the sinc function. In other words, he favours a trivially truncated sinc filter (which is of course also windowed, just with a rectangular window). It is obviously true that the longer such a filter is made, the closer the output will resemble that of an ideal interpolation. What he refuses to admit is that for a given filter length, a truncated sinc function is not the best choice. A couple of graphs should illustrate this.

First we look at the frequency response of a truncated sinc filter of various lengths:

As we can see here, 100,000 taps are needed to achieve anything reasonably good, and for hi-fi performance, a full 1 million are required. This is pretty much consistent with observed performance of Chord products.

Now we take the same truncated sinc functions and apply a Kaiser window (β = 8):

The frequency response is much improved, gaining more than 40 dB of stopband rejection at the expense of a slightly less steep transition. Now even the shortest filter, with 1,000 taps, gives acceptable performance. By choosing different window functions, it is possible to tailor the response depending on which aspects are most important in a given application.

Why, then, does Rob Watts insist on using his "pure" sinc function? That is a good question. Maybe he really believes it's better. Maybe he simply figures this purism spiel will help his sales. We will probably never know.

 

[tmtomh]

(I'm not really an expert in the area, so take with a grain of salt)
One rather inefficient way of upsampling with non-integer ratios is:

1. reduce the ratio: 96'000 / 44'100 -> 320 / 147
2. upsample by inserting 319 zeros between the samples - so far the original samples are preserved. The resulting sample rate is 14'112'000 (this is the Least Common Multiple of 44'100 and 96'000)
3. apply filtering
4. downsample by picking every 147th sample - most of the original samples are lost. The resulting sample rate is 96'000

I thought it was rather clear from the post that it is just curiosity.


So, we meet again

Ack! I soon as I saw you in my notifications, I was like, "Oh, yes, it was danadam!" I won't forget again, you can be sure of that!

 

[danadam]

In case anyone wants to experiment with how well the original samples are preserved when doing integer ratios:

sox -r48k -n -b24 A_48.wav synth 60 pink norm -3 sinc -20k norm -3 fade 1 0 1
sox A_48.wav B_96.wav rate -v 96k
sox B_96.wav -r48k C_48.wav downsample 2
sox -m -v 1 A_48.wav -v -1 C_48.wav D_null.wav
sox D_null.wav -n stats 2>&1 | grep "Pk lev dB"

1. generate pink noise at 48 kHz sampling rate, bandlimited to 20 kHz - we get A
2. convert to 96 kHz - we get B
3. downsample by picking every second sample - we get C
4. subtract A and C - we get D
5. show peak level in D

Run 10 times:

]$ for i in $(seq 10); do ./run.sh ; done
Pk lev dB    -120.41
Pk lev dB    -122.91
Pk lev dB    -122.91
Pk lev dB    -121.57
Pk lev dB    -121.57
Pk lev dB    -120.41
Pk lev dB    -118.47
Pk lev dB    -118.47
Pk lev dB    -124.49
Pk lev dB    -122.91

You can play with bandlimit in "sinc" effect from the first line to see how it affects results.

 

[Music1969]

Now we take the same truncated sinc functions and apply a Kaiser window (β = 8):

I searched this post where he mentioned Kaiser filter:

Watts Up...?

My advice over many years has been not to use up-samplers, but to always feed my DACs with bit perfect data, as the WTA algorithm would always do a much better job than conventional algorithms in terms of recovering transient timing more accurately and hence better sound quality and musicality...

www.head-fi.org

and this

CHORD ELECTRONICS DAVE

I can't imagine Dave will replace my berkeley reference dac , if watts listen to my berkeley reference he will increase the taps to 400 K to beat it . Still I can't wait to hear it .

www.head-fi.org

So it appears he agrees Kaiser filter is good

But he thinks his WTA filter is better (which is 50% Whittaker-Shannon interpolation)

 

[Music1969]

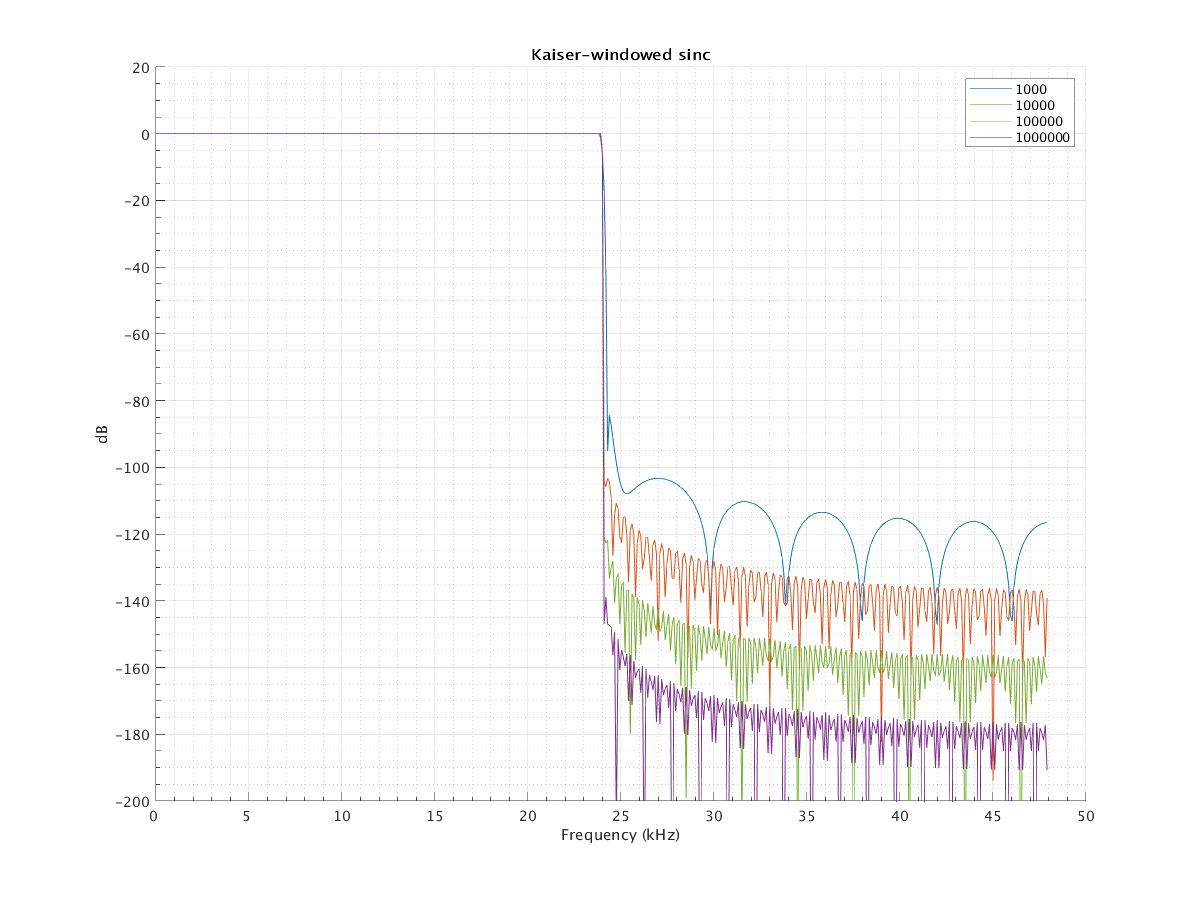
In case anyone wants to experiment with how well the original samples are preserved when doing integer ratios:

Thanks!

This example is mostly relevant in the case of downsampling right?

Not for only upsampling at playback (D to A) side ?

 

[earlevel]

You don't need an ideal one, any windowed sinc preserve input samples.
This property is particularly important for half band filter ( for x2 upsampler) : you only need to compute half of the output samples, the other half are just the input samples.

Gee, now I'm wondering if I'm misunderstanding, after mansr changed his mind and you said this, so I'm risking a bout of hoof in mouth, but...

First, when you say "any windowed sinc preserve input samples"...it seems "windowed" doesn't matter—we can't realize a non-windowed sinc filter (and if we could, it wouldn't change the assertion anyway). I'm not being nit-picky, just mentioning it in case it makes obvious that I'm misreading.

Now, a half-band filter has zeros aligning with the sample periods, yes. But we often have the corner frequency below half. In that case, the zeros aren't aligned, we have lobes. That is, put 0..0,1,0..0 into such an upsampling filter, you don't get the same (with more zeros) out. The impulse response is not a lone 1 sample. So I would say input samples are not preserved (except in special cases like half-band). No?

 

[earlevel]

In case there was any doubt, nothing in that post makes any sense.

this ^^^^

Seriously, it hurts to read that he's spent four decades working on "the theory of interpolation", while seemingly saying two things demonstrably wrong per sentence for a good deal of that. I had to come back to it later and force myself to get through it. There was no payoff. Weird how if you say esoteric things about digital audio, implying that the mainstream is missing some subtle truth of nature, while mixing in words like "transparency"—and you do it with conviction—you will get a following.

 

[tcli]

Gee, now I'm wondering if I'm misunderstanding, after mansr changed his mind and you said this, so I'm risking a bout of hoof in mouth, but...

You perfectly understand

First, when you say "any windowed sinc preserve input samples"...it seems "windowed" doesn't matter—we can't realize a non-windowed sinc filter (and if we could, it wouldn't change the assertion anyway). I'm not being nit-picky, just mentioning it in case it makes obvious that I'm misreading.

Any (FIR) filter where every Nth coefficient is zero will indeed preserve the input samples when used as an interpolation filter for upsampling by a factor N.

Any filter that have the property below will preserve input sample. But if you add the constrains : being low pass and symmetric , you will end up with a windowed sinc.

Now, a half-band filter has zeros aligning with the sample periods, yes. But we often have the corner frequency below half. In that case, the zeros aren't aligned, we have lobes. That is, put 0..0,1,0..0 into such an upsampling filter, you don't get the same (with more zeros) out. The impulse response is not a lone 1 sample. So I would say input samples are not preserved (except in special cases like half-band). No?

Yes, if for example, you design your filter with Parks–McClellan algorithm, it will have no chance to preserve input sample.

 

[tcli]

CHORD ELECTRONICS DAVE

I can't imagine Dave will replace my berkeley reference dac , if watts listen to my berkeley reference he will increase the taps to 400 K to beat it . Still I can't wait to hear it .

www.head-fi.org

Interesting, so WTA does not preserve input samples ...

 

[earlevel]

Interesting, so WTA does not preserve input samples ...

Yes, interest considering what he said before. (Not as many, um, questionable things in that post as before, but there he is again with his assertion that transients are moving around. I want to give him the benefit of the doubt, that I'm misunderstanding his point, but it's hard based on what he types—can anyone point me to a more detailed explanation of what he's going on about?)

I get that we're just discussing peoples' views on preserving input samples, and not necessarily anyone here, but I'll go on record with my view: I think it's silly to make decisions based on preserving samples, which were approximations anyway. I don't see much point in pronouncing them "golden", then mixing in as many or more approximated samples (for the upsampling process, 2x, 4x, etc.) derived from them. And heaven help us if there is any gain change in the digital domain, or other filter, if that's your view. This is basic math—you can't end up with more precision than you started with after performing an operation, you can only try to keep what you had by doing your math properly.

So yeah, things like halfband filters are useful tools, with characteristics that may or may not be a problem, depending on how they are used. But to pick them when they aren't the best thing, in order to maintain these supposedly golden samples...I just don't see the point of that. The goal should be to keep calculation errors from creeping into the 24 bits that go out to the DAC (or at least the lsb, which will have relatively large errors from the truncation anyway).

 

[earlevel]

I don't have time to watch the video, but you don't keep the original samples in either case, given a fullrange signal, for any practical digital filter.

What is true is that upsampling by integer ratios involves way less math. To upsample by 2x for example, you just insert zeros between each sample and then apply a low-pass filter. This probably sounds strange and counter-intuitive if you're not used to signal processing, but after you're done filtering, the zeros get "magically" transformed into interpolated values. (Of course it isn't magic, it's just a beautiful result of how the math works.)

Because any practical low-pass filter has a transition band of nonzero width, some of the original samples may get changed during this process, if the input signal is fullrange.

When you upsample by non-integer ratios, the math is many times more complicated, and none of the original samples will be preserved (and of course they wouldn't -- where in the time domain would those samples be?).

That's a really good answer. I just feel like peeling the onion back another layer, and say—for no other reason that nerdom...

There are basically two reasons why integer ratios (like converting from 44.1 to 48 by upsampling 160x, downsampling 147x). One is that it's conceptually simple. The other is that you can use a pre-calculated table (typically windowed sinc) because all the points you calculate while upsampling are in the sample relative places between samples. Classical DSP text books don't even hint that there is a way to change sample rates by other than integer ratios, that that's why the math is more difficult—you have to roll your own.

But, if you want to do it directly, it's really not complicated to go directly from one rate to another in one step. You have evenly spaced input samples to work with either way. Upsampling by a factor of 3, you know the new samples will be a third of the way between input samples, and that will continue to be true as you move forward to new input samples. For 44.1k to 48k, though, they land in different places each time, in a pattern that takes a long time to repeat (and never for irrational factors, but the integer ratio method won't work there either).

However, that's just a distraction, it really hasn't gotten more complicated mathematically. You know where the next sample lands, you know where it is relative to the input, so you know where the values are that you need to convolve the input with lie on a continuous windowed sinc function. The only difference is that you need to calculate all the source points of the windowed sinc "on the fly".

Though you could calculate a large table beforehand for 48/44.1, to handle all the phases needed. Managing the phases would add a little complexity, but it can be argued that it's no more complex than the integer up/down method and optimizing away the zeros. Just a little rougher to wrap your head around.

But, why not make this work for any sample rate changes—including irrational factors that you can't do with integer ratios? That brings it to the root of the problem, and the reason for the ("polyphase filter") tables to begin with. You'd need to calculation points from the windowed sinc function on the fly, and the worst offender is sin(). However, there is a shortcut for which the only penalty is pre-computing a very large windowed sinc (or other filter) table. Since the function is very smooth, we can oversample the function by whatever factor we need to meet a given accuracy while pre-computing the table, then use it to interpolate the exact points we need for each new sample. Because of the smoothness, linear interpolation can be adequate for the table look up. Credit to Julius O. Smith for pointing this out.

OK, thanks for letting me digress...maybe I'll write a more detailed article on my website on the topic...