This is a review and detailed measurements of JDS Labs Atom Headphone Amplifier. It was kindly sent on loan by JDS Labs in advance of its formal announcement and availability this week. It retails for USD $99. As such, I will be comparing its performance to other $99 amplifiers such as Schiit Magni 3 and Monoprice Liquid Spark.
The Atom is a nice departure from the JDS O2 in having proper RCA connectors in the back and 1/4 headphone jack in front (and 3.5mm in the back):

The enclosure is plastic and lightweight but is stable enough to not move around with the weight of cables.
As you see in the comparison above, it is about 10% wider and deeper than O2. The volume control feels slightly less good than the O2 with the latter having more of a "hydraulic" feel.
There is not much else to say about it so let's get into the measurements and see how she does.
Measurements
I started my measurements with a dashboard view of unity gain with 2 volts in, and nearly 2 volts out:
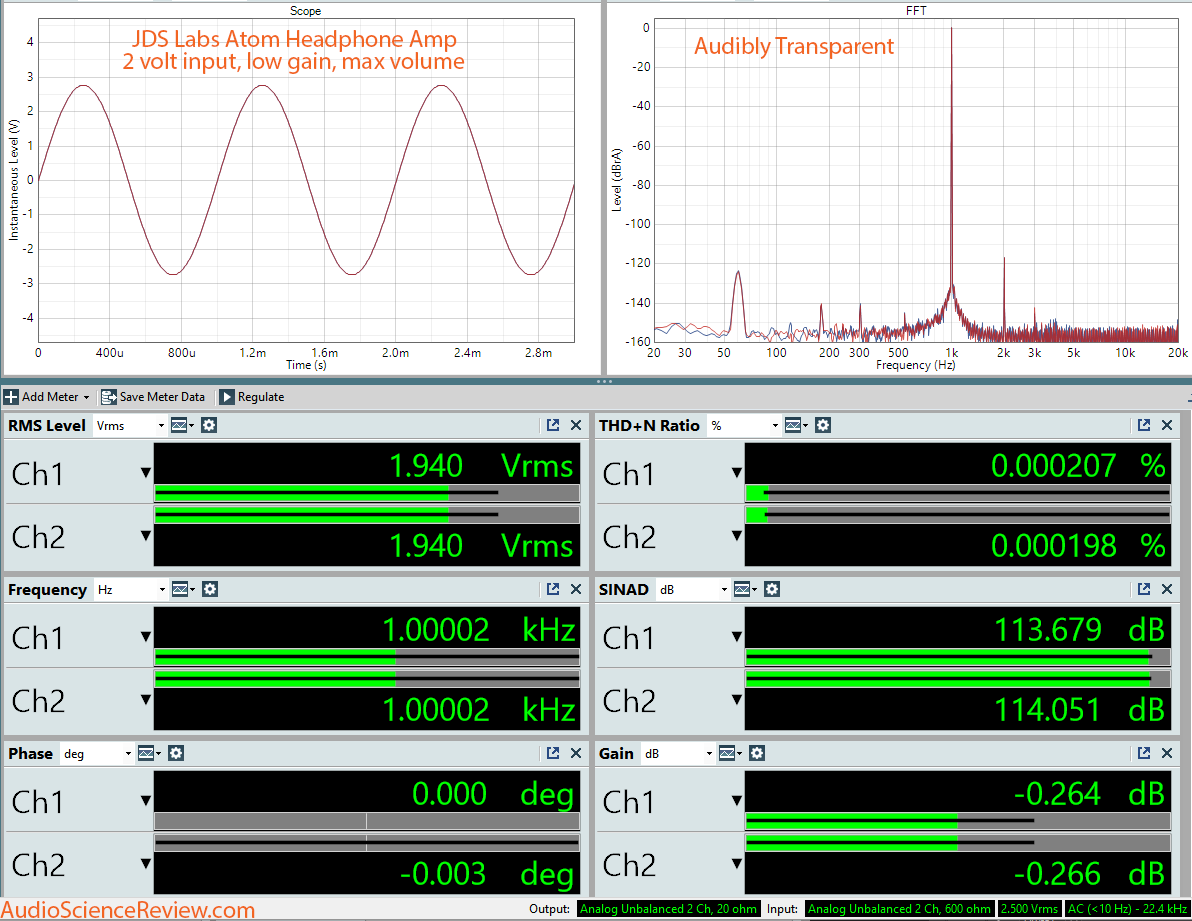
Are you seeing what I am seeing? SINAD of 114 dB??? In a $99 device? Are you kidding me? Running the same test on Monoprice Liquid Spark struggled to get to 100 dB. This is a good 15 dB better performance.
With our best case hearing dynamic range of 116 dB, this is provably audibly transparent.
At lower output levels of say 1 volt (not shown), the distortion goes so far down that the mains spike at 60 Hz dominates. Since our hearing sensitivity there is some 50 dB higher, this device becomes essentially distortionless.
This is in low gain by the way. High gain was not quite as good.
Since some of you have been asking, I also added the phase information. As we see, the differential of 0.003 degree means there is nothing there to worry about.
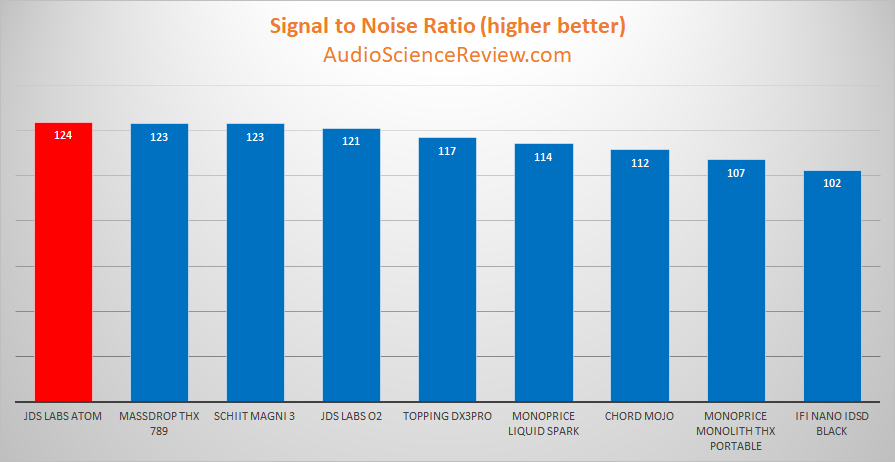
Signal to noise ratio is likewise exceptional:
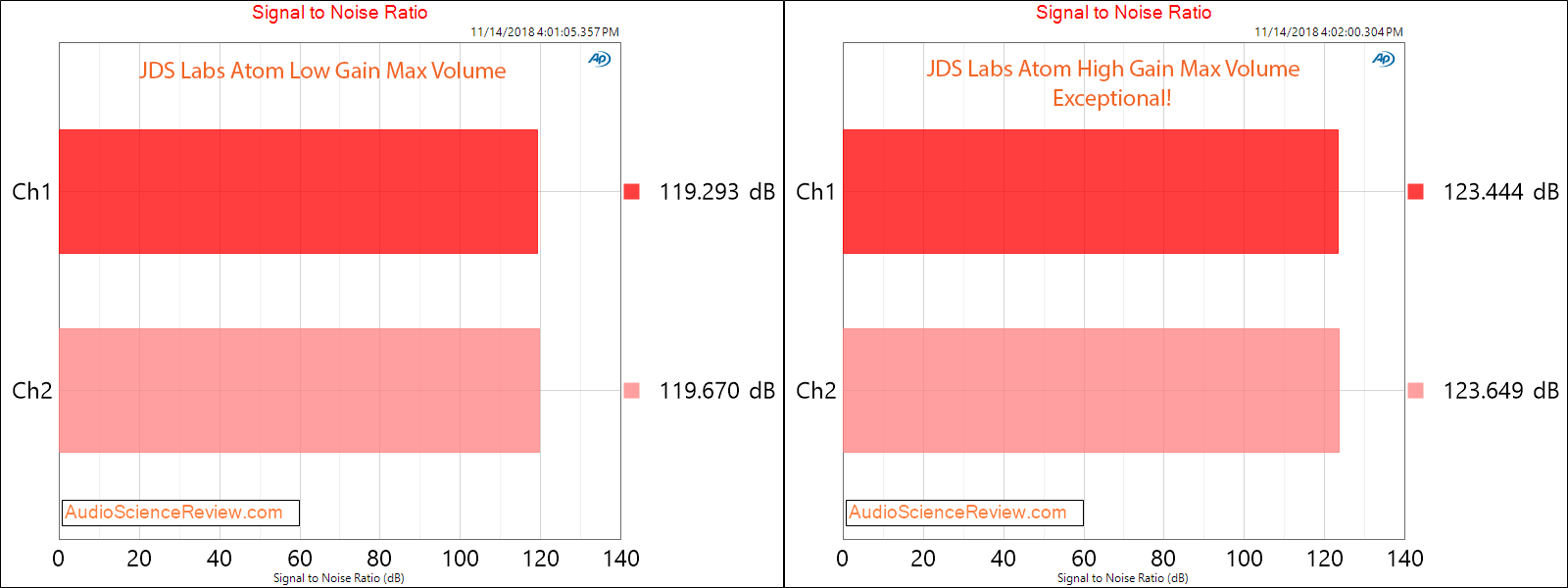
123 dB in high gain! Wow.
Yes, this is Massdrop THX AAA 789 territory. And no, the Atom does not use THX technology:
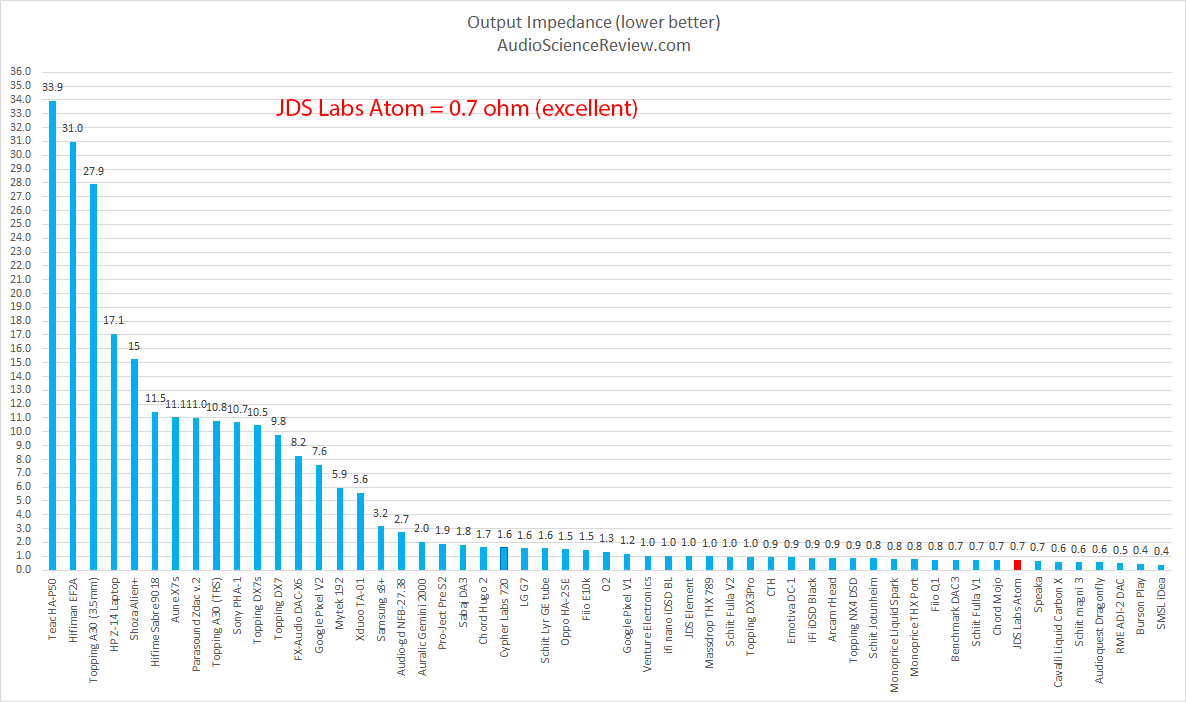
Output impedance is comfortably low at 0.7 ohm:
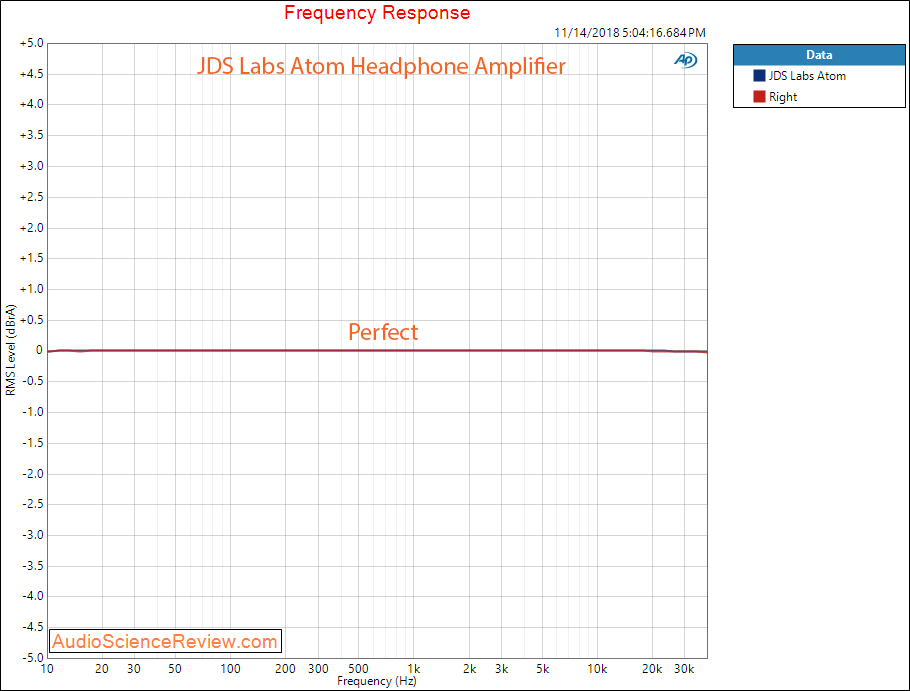
Frequency response is dead flat to 40 kHz:
Let's see how much power there is compared to Monoprice Liquid Spark and Schiit Magni 3. Note that I have refined these tests and used better setup to get the best performance (Monoprice performance improved but not Schiit Magni 3 compared to my previous review):
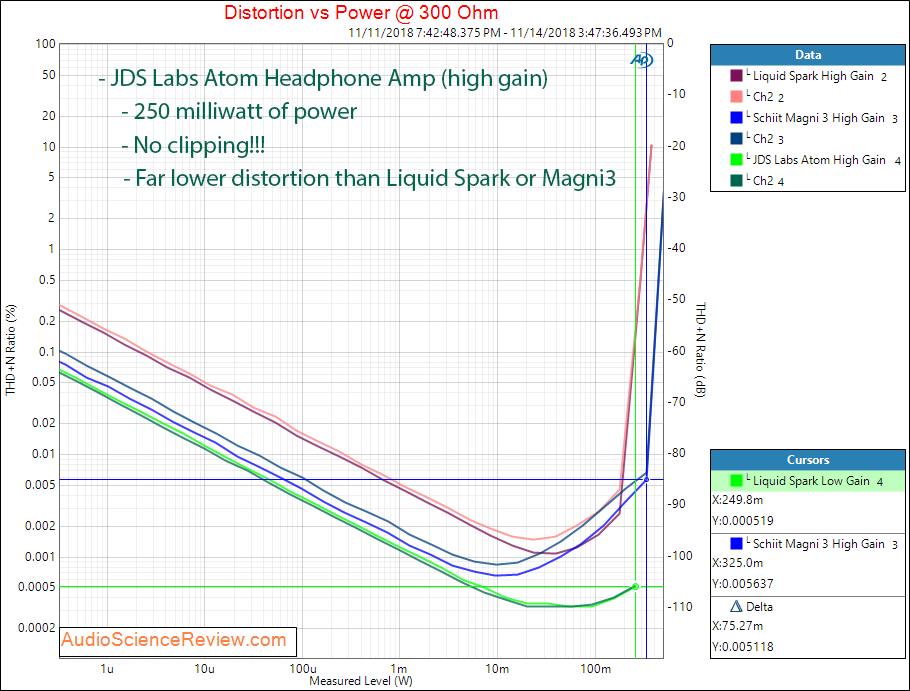
We get 250 milliwatts of power with essentially no distortion or clipping. At max power, distortion is incredibly low 0.0005% (SINAD 106 db). This is an order of magnitude better than Schiiit Magni 3. And is more power than Liquid Spark manages.
Switching to 33 ohm load we get:
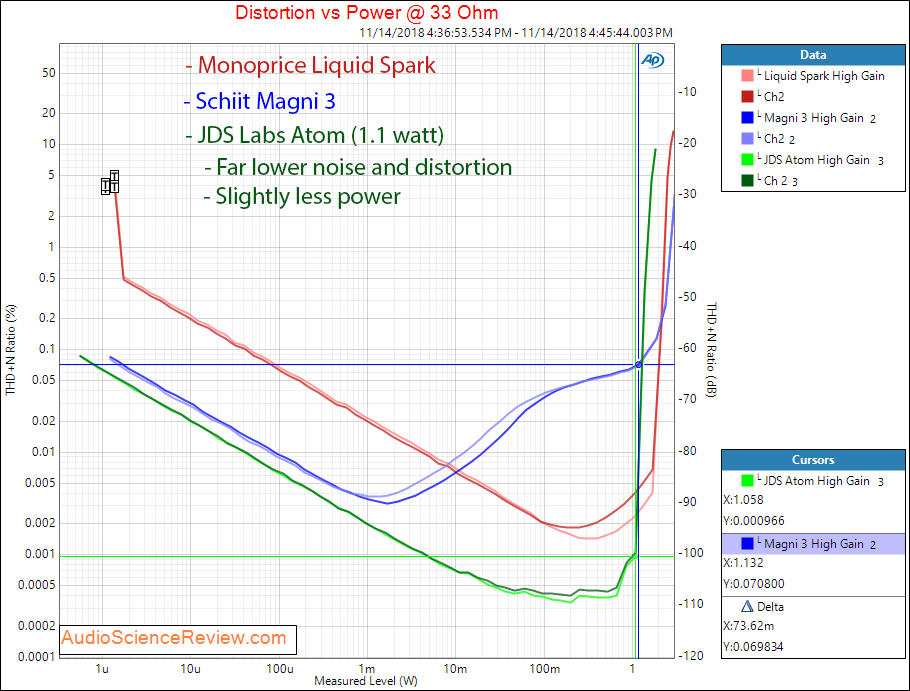
Similar picture emerges. We have slightly less power output but much, much lower distortion and noise. You get one full watt of power at just 0.0009% distortion. Incredible.
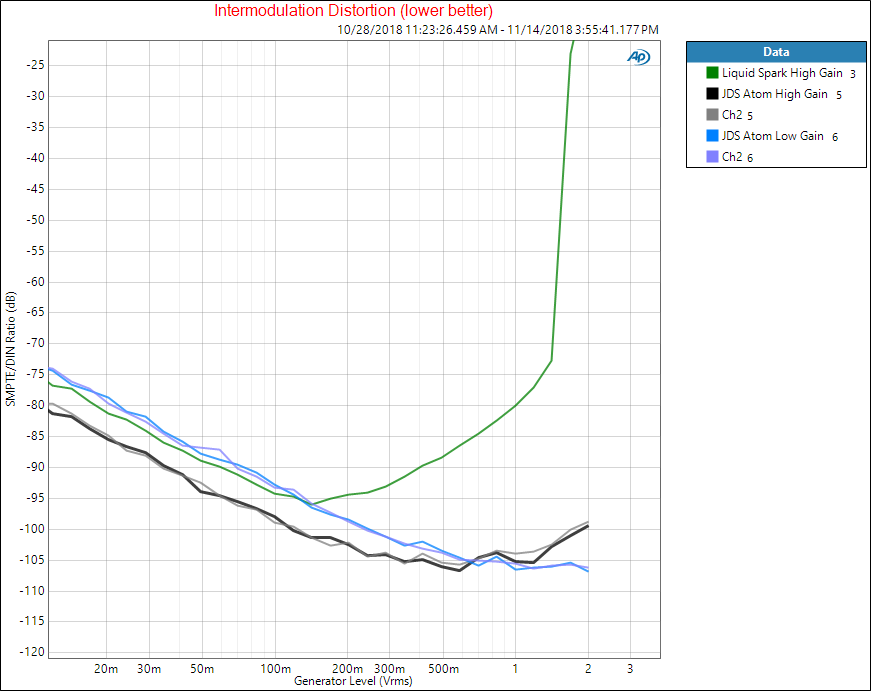
Here is the intermodulation distortion versus level:
Finally, here is the channel imbalance versus volume position:
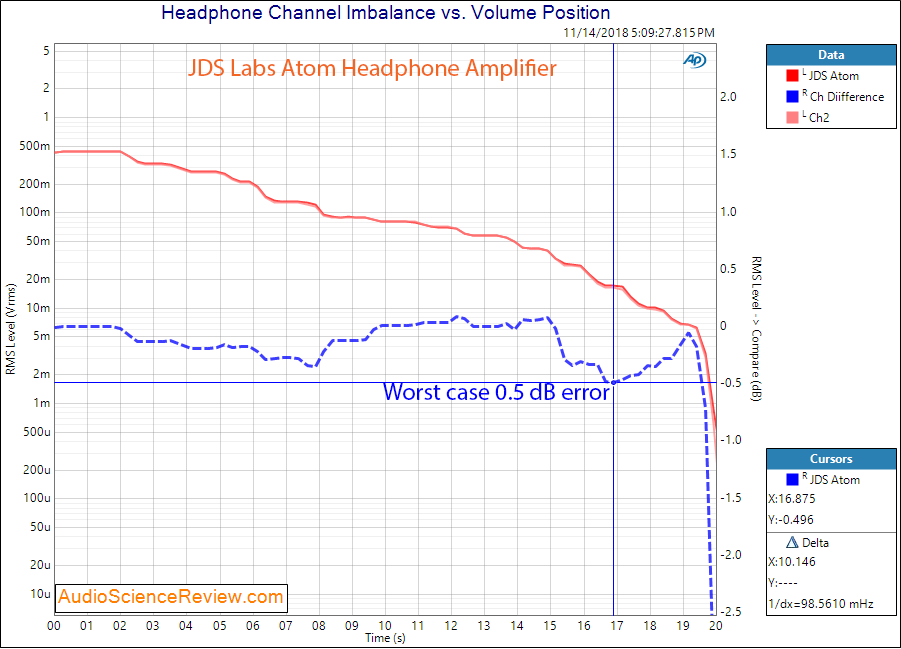
Worst case error occurs as usual close to the end of the range. The above is in high gain mode. Switching to low gain should reduce the impact here.
Listening Tests
There was no shortage of power driving my Sennheiser HD-650s. Comfortable level as 11:00 to 12:00 o'clock. As shown in measurements, there is no rise in distortion up to max volume at 5:00 at which time, you are hearing thundering bass and control of the drivers.
Switching to Hifiman HE-400i was the same, resulting in some of the cleanest, best bass I have heard on these headphones.
Playing my audiophile track list brings joy and satisfaction with every detail audible. It is so nice to be free of amplification distortion even during the loudest segments.
Channel imbalance was only audible with my headphones at almost zero volume level.
Conclusions
We have arrived at the golden age of headphone amplification folks. What JDS Labs Atom delivers for just $99 is astonishing. Performance is without fault. Plenty of power is available for even high impedance headphones like Sennheiser HD-650. We are talking clean, clean, power.
During this testing I asked John from JDS Labs how he had achieved this level of performance. His answer: "just many prototypes and lessons learned throughout the year." In other words, good engineering. Use a closed loop measurement system as JDS does and you are golden as we see here.
Official announcement of product is tomorrow (11/15). Shipment is shortly after (not sure if I have permission to say when).
Needless to say, JDS Labs Atom gets one of my highest recommendations. Given their excellent support, activity in forums, and bargain $99 price, every audiophile with a headphone needs to get one of these.
As always, all questions, comments and criticism is welcome.
-----
If you like this review, please consider donating funds for these types of hardware purchases using Patreon (https://www.patreon.com/audiosciencereview), or upgrading your membership here though Paypal (https://audiosciencereview.com/foru...eview-and-measurements.2164/page-3#post-59054).
The Atom is a nice departure from the JDS O2 in having proper RCA connectors in the back and 1/4 headphone jack in front (and 3.5mm in the back):
The enclosure is plastic and lightweight but is stable enough to not move around with the weight of cables.
As you see in the comparison above, it is about 10% wider and deeper than O2. The volume control feels slightly less good than the O2 with the latter having more of a "hydraulic" feel.
There is not much else to say about it so let's get into the measurements and see how she does.
Measurements
I started my measurements with a dashboard view of unity gain with 2 volts in, and nearly 2 volts out:
Are you seeing what I am seeing? SINAD of 114 dB??? In a $99 device? Are you kidding me? Running the same test on Monoprice Liquid Spark struggled to get to 100 dB. This is a good 15 dB better performance.
With our best case hearing dynamic range of 116 dB, this is provably audibly transparent.
At lower output levels of say 1 volt (not shown), the distortion goes so far down that the mains spike at 60 Hz dominates. Since our hearing sensitivity there is some 50 dB higher, this device becomes essentially distortionless.
This is in low gain by the way. High gain was not quite as good.
Since some of you have been asking, I also added the phase information. As we see, the differential of 0.003 degree means there is nothing there to worry about.
Signal to noise ratio is likewise exceptional:
123 dB in high gain! Wow.
Yes, this is Massdrop THX AAA 789 territory. And no, the Atom does not use THX technology:
Output impedance is comfortably low at 0.7 ohm:
Frequency response is dead flat to 40 kHz:
Let's see how much power there is compared to Monoprice Liquid Spark and Schiit Magni 3. Note that I have refined these tests and used better setup to get the best performance (Monoprice performance improved but not Schiit Magni 3 compared to my previous review):
We get 250 milliwatts of power with essentially no distortion or clipping. At max power, distortion is incredibly low 0.0005% (SINAD 106 db). This is an order of magnitude better than Schiiit Magni 3. And is more power than Liquid Spark manages.
Switching to 33 ohm load we get:
Similar picture emerges. We have slightly less power output but much, much lower distortion and noise. You get one full watt of power at just 0.0009% distortion. Incredible.
Here is the intermodulation distortion versus level:
Finally, here is the channel imbalance versus volume position:
Worst case error occurs as usual close to the end of the range. The above is in high gain mode. Switching to low gain should reduce the impact here.
Listening Tests
There was no shortage of power driving my Sennheiser HD-650s. Comfortable level as 11:00 to 12:00 o'clock. As shown in measurements, there is no rise in distortion up to max volume at 5:00 at which time, you are hearing thundering bass and control of the drivers.
Switching to Hifiman HE-400i was the same, resulting in some of the cleanest, best bass I have heard on these headphones.
Playing my audiophile track list brings joy and satisfaction with every detail audible. It is so nice to be free of amplification distortion even during the loudest segments.
Channel imbalance was only audible with my headphones at almost zero volume level.
Conclusions
We have arrived at the golden age of headphone amplification folks. What JDS Labs Atom delivers for just $99 is astonishing. Performance is without fault. Plenty of power is available for even high impedance headphones like Sennheiser HD-650. We are talking clean, clean, power.
During this testing I asked John from JDS Labs how he had achieved this level of performance. His answer: "just many prototypes and lessons learned throughout the year." In other words, good engineering. Use a closed loop measurement system as JDS does and you are golden as we see here.
Official announcement of product is tomorrow (11/15). Shipment is shortly after (not sure if I have permission to say when).
Needless to say, JDS Labs Atom gets one of my highest recommendations. Given their excellent support, activity in forums, and bargain $99 price, every audiophile with a headphone needs to get one of these.
As always, all questions, comments and criticism is welcome.
-----
If you like this review, please consider donating funds for these types of hardware purchases using Patreon (https://www.patreon.com/audiosciencereview), or upgrading your membership here though Paypal (https://audiosciencereview.com/foru...eview-and-measurements.2164/page-3#post-59054).
