Let's develop an ASR inter-sample test procedure for DACs!

[edechamps]

An elegant one would be for the player to scan your files at import and flag the compensation in the form of metadata.

For those interested, foobar2000 has this feature built-in:

 

[pma]

The peak amplitude of any waveform represented in PCM will exceed the amplitude of the samples unless a given sample happens to fall exactly on a peak. This is a fundamental property of PCM encoding. The playback hardware should be capable of reproducing any reasonable band-limited non-clipped waveform that has been encoded in PCM. 3 dB of headroom is sufficient.

Some DACs invert the audio when an intersample peak occurs. The inversion can extend before and after the actual peak (due to the length of the FIR filter) The polarity inversion is caused by a failure to recognize an arithmetic overflow in the DSP. DACs that have an inversion problem, produce very nasty distortion. It is very audible. I believe some of these have been tested on ASR, but this problem was missed.

Excellent points, @John_Siau . Please let me demonstrate.

1) DAC input digital signal that has zero count of clipped samples (over the entire 30 seconds length)


2) DAC analog output in the part where sample values are close to peaks

3) DAC analog output where sample values do not meet the peaks

Clipping + inversion. Input digital stream is the same. Screens are just different portions of the same record. DAC output sampled at 1.563 MHz.

 

[KSTR]

@pma, could you please show the input signal, and also show the last plot again, but with reduced input amplitude?
While the waveform is not exactly what would be expected, I don't see clipping and inversion.What I see is the ripple increasing towards the falling edge where it has a maximum, then decreasing ripple amplitude. But the ripple doesn't look like being clipped....

 

[pma]

@pma, could you please show the input signal,

I am not sure that I understand properly. Below is the AA analysis of the full length digital signal that was sent to the DAC. There is a zero occurrence of "possibly clipped samples". No sample value equals to or exceeds +/-32767.

I don't see clipping

one more at higher time resolution

 

[KSTR]

@pma, thanks, now I see the clipping ;-)
wrt waveform, what I meant is the sample-train, basically a square-wave but which points or frequency exactly? Below example for a 300Hz square:

 

[pma]

This is the example of clipping due to improperly created recording. This is NOT the DAC clipping.

 

[pma]

@pma, thanks, now I see the clipping ;-)
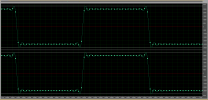
wrt waveform, what I meant is the sample-train, basically a square-wave but which points or frequency exactly? Below example for a 300Hz square:

OK, I hope I understand now. 1kHz signal at 48kHz Fs, below the spectrum and sample values and brickwall reconstruction by AA.

I do not think that it is an "invalid" digital signal .

 

[markstein]

Would be interesting to see how the imtersample clipping distortion profile is with different brickwall filter settings. Could that be one reason why some people prefer "slower" brickwall filters? The filter ringing itself should be inaudible.

 

[Scytales]

1. Lossy compression systems (such as MP3) tend to create an abundance of intersample overs. A DAC that clips intersample overs will sound especially bad when playing MP3s. MP3 compression can add intersample overs even when none were in the original non-compressed track.

By your observation, are perceptual codings such as DTS or Dolby Digital also affected?

 

[pma]

also show the last plot again, but with reduced input amplitude?

The clipping at top and bottom of the waveform has disappeared when the DAC output was digitally attenuated (it was probably DAC analog output clipping). But, the strange "rhino nose" at the rising and falling edges has remained there.

Would be interesting to see how the imtersample clipping distortion profile is with different brickwall filter settings. Could that be one reason why some people prefer "slower" brickwall filters? The filter ringing itself should be inaudible.

I agree, I may do it later, it will need some time.

 

[pma]

Would be interesting to see how the imtersample clipping distortion profile is with different brickwall filter settings.

Not IS, but just clipping with another DAC is shown below:

I have to add that these issues vary with replay conditions - native sampling frequency, oversampling etc. The result depends on WDM or Wasapi EXCL choice and Windows control panel sound settings for the DAC. Too many variables to give one simple answer.

 

[miero]

A random white noise stored in PCM might require more than 8dB attenuation to not clip when resampling. The value depends on the selected filters:

SoX very high quality (band-width 95%), linear phase:

$ sox -R -r 44100 -n -n synth 100 white vol -10dB rate -v $((8*44100)) stats 2>&1 | grep "Pk lev"
Pk lev dB -3.91

10 - 3.91 = 6.09 dB overshoot

SoX very high quality (band-width 95%), intermediate phase:

$ sox -R -r 44100 -n -n synth 100 white vol -10dB rate -vI $((8*44100)) stats 2>&1 | grep "Pk lev"
Pk lev dB -2.42

10 - 2.42 = 7.58 dB overshoot

SoX very high quality (band-width 95%), minimum phase:

$ sox -R -r 44100 -n -n synth 100 white vol -10dB rate -vM $((8*44100)) stats 2>&1 | grep "Pk lev"
Pk lev dB -1.99

10 - 1.99 = 8.01 dB overshoot


The issue seems to be more caused by high-frequency content, but even if we use steep sinc filter to cut everything above 10kHz, there are still some overshoots:

$ sox -R -r 44100 -n -n synth 100 white vol -10dB sinc -10k rate -vM $((8*44100)) stats 2>&1 | grep "Pk lev"
Pk lev dB -6.56

10 - 6.56 = 3.44 dB overshoot for the SoX very high quality (band-width 95%), minimum phase.

 

[markstein]

Let's develop an ASR inter-sample test procedure for DACs!

Real life example

audiosciencereview.com

This looks pretty much as expected (different impulse responses) and is not what I meant.

Question is whether different brickwall filter slopes lead to different distortion profiles caused by intersample clipping.

When using minimum phase filters, I would expect the distortion happening after the clipping signal, probably being masked by the signal. When using linear phase filters, due to their symmetrical impulse response, distortion is also happening before and may be more audible.

Does this make sense?

 

[pma]

Question is whether different brickwall filter slopes lead to different distortion profiles caused by intersample clipping.

The question is what you get from such plots. Sudden, even shortest change in the signal continuity has always dramatic effect on signal spectrum. Now we are not in the steady state sine wave area.

 

[markstein]

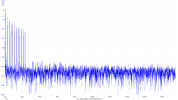
A random white noise stored in PCM might require more than 8dB attenuation to not clip when resampling. The value depends on the selected filters:

SoX very high quality (band-width 95%), linear phase:

10 - 3.91 = 6.09 dB overshoot

SoX very high quality (band-width 95%), intermediate phase:

10 - 2.42 = 7.58 dB overshoot

SoX very high quality (band-width 95%), minimum phase:

10 - 1.99 = 8.01 dB overshoot


The issue seems to be more caused by high-frequency content, but even if we use steep sinc filter to cut everything above 10kHz, there are still some overshoots:

10 - 6.56 = 3.44 dB overshoot for the SoX very high quality (band-width 95%), minimum phase.

This seems to be in line with "more overshoot" visible in minimum phase impulse response

 

[KSTR]

Would be interesting to see how the imtersample clipping distortion profile is with different brickwall filter settings. Could that be one reason why some people prefer "slower" brickwall filters? The filter ringing itself should be inaudible.

This might very well be the case. The gentler the transition into the stop-band of the filter, the lower the peaks and the less likely they undergo clipping or nastier artefacts.
Let's go back to NOS (ZOH output) with analog filter (also correcting the NOS HF roll-off), haha!

 

[Whoareyou]

For those interested, foobar2000 has this feature built-in:

View attachment 396193

JRiver also has this feature built-in:

NEW: Improved audio analysis and volume leveling (R128)

NEW: Improved audio analysis and volume leveling (R128)

yabb.jriver.com

 

[pma]

could you please show the input signal, and also show the last plot again, but with reduced input amplitude?

I think I got your point, Klaus. Below is the DAC digital input signal, but attenuated of -1.4dB. The portion where samples do not meet reconstructed wave peaks is chosen. Still waiting for analog output with this reduced input amplitude, right?
Later, but I am quite sure it will be behaving properly.

 

[miero]

Resample attempt on a track of Steely Dan mentioned by John Siau:

SoX very high quality (band-width 95%), linear phase:

$ sox Steely\ Dan\ -\ 01.\ Gaslighting\ Abbie.flac -n vol -10dB rate -v $((8*44100)) stats
Overall Left Right
Pk lev dB -9.20 -9.27 -9.20
RMS lev dB -26.40 -26.17 -26.64

10 - 9.2 = 0.8 dB overshoot

SoX very high quality (band-width 95%), intermediate phase:

$ sox Steely\ Dan\ -\ 01.\ Gaslighting\ Abbie.flac -n vol -10dB rate -vI $((8*44100)) stats
Overall Left Right
Pk lev dB -7.47 -7.98 -7.47
RMS lev dB -26.40 -26.17 -26.64

10 - 7.47 = 2.53 dB overshoot

SoX very high quality (band-width 95%), minimum phase:

$ sox Steely\ Dan\ -\ 01.\ Gaslighting\ Abbie.flac -n vol -10dB rate -vM $((8*44100)) stats
Overall Left Right
Pk lev dB -7.37 -7.37 -7.58
RMS lev dB -26.40 -26.17 -26.64

10 - 7.37 = 2.63 dB overshoot

 

[krabapple]

The assumption that "a huge amount of music ... doesn't have this problem" is incorrect.

The vast majority of 44.1 kHz recordings have intersample peaks that exceed 0 dBFS. Curiously, tracks with minimal compression can have some of the highest and most frequent intersample peaks. See my application note on this topic: Intersample Overs in CD Recordings

When intersample peaks overload a DAC, a DSP, or an ASRC, the distortion reaches very high levels and it is often non-harmonic. This playback defect is huge compared to all of the other THD, IMD, and SNR issues in playback hardware.

I would assert that the intersample over test is the single most important test from the standpoint of detecting audible defects in a digital audio product.

The cure requires a 3-dB loss in SNR. This a small price to pay for eliminating the single most audible defect with most DACs, especially when most modern DACs have a higher SNR than the power amplifiers that they will be driving.

Your document says:
"Nevertheless, in a little over 5 minutes, this track has 559 intersample overs on the left track and 570 on the right track for a total of 1129. This means that there are about 3.7 intersample overs per second. "

What;s left out is that each sample is 1/44K th of a second in duration. Individually these aren't likely to be audible at all.

If there are consecutive overs, and the consecutive run is long enough, no doubt it can be audible. But that isn't established here.

Your doc claims that the overs add unnatural 'sparkle' to the snare in Gaslighting Abby, but that seem to be a subjective claim, with no DBT data backing it up.