Hi
I thought I'd create a new thread about this topic.
I originaly posted my question here
Detailed analysis will be in next post
Here-under is the original question:
This "gain" is the level drop for noise in the display (or for the distortion analysis).
But it's not impacting SNR or SINAD, or does it ?
Actually, I see some impact of FFT size on SNR, but that's nowhere near linear.
And I have no clue what's causing that.
Example of a Loopback FFT Size/SNR
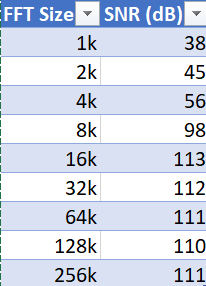
And this looks quite random, on top of it: I've seen 128k being higher than 32k for other configurations, as an example.
Does anyone know why ?
At lower FFT size, it looks like there is high low frequency noise, due to the fuzzy frequency resolution.
But why do we see variation above 16k points ?
Notes: sampling frequency in this example was 48kHz
I get the same figures for the same config anytime
I also read the exact same values from Multi Instrument and from REW
I thought I'd create a new thread about this topic.
I originaly posted my question here
Detailed analysis will be in next post
Here-under is the original question:
HiYes. Here is the amount of "FFT gain" (measurement noise reduction) for different number of audio samples used:
32K = 42 dB
256K = 51 dB
1 million = 57 dB
The actual dB is a few dB different since it also includes the effect of the FFT Window. But is not material in grand scheme of things.
This "gain" is the level drop for noise in the display (or for the distortion analysis).
But it's not impacting SNR or SINAD, or does it ?
Actually, I see some impact of FFT size on SNR, but that's nowhere near linear.
And I have no clue what's causing that.
Example of a Loopback FFT Size/SNR
And this looks quite random, on top of it: I've seen 128k being higher than 32k for other configurations, as an example.
Does anyone know why ?
At lower FFT size, it looks like there is high low frequency noise, due to the fuzzy frequency resolution.
But why do we see variation above 16k points ?
Notes: sampling frequency in this example was 48kHz
I get the same figures for the same config anytime
I also read the exact same values from Multi Instrument and from REW
Last edited: