mononoaware
Addicted to Fun and Learning
- Joined
- Apr 6, 2021
- Messages
- 816
- Likes
- 669
So this is what my EQ setting on NW-A50 Series Walkman has looked like for the past few years and everything sounds “just right”, do you think my hearing is broken?
The one in image (Custom 1) is for over-ear headphones, but the saved IEM equalizer setting (Custom 2) looks identical except -2dB @ 60hz.
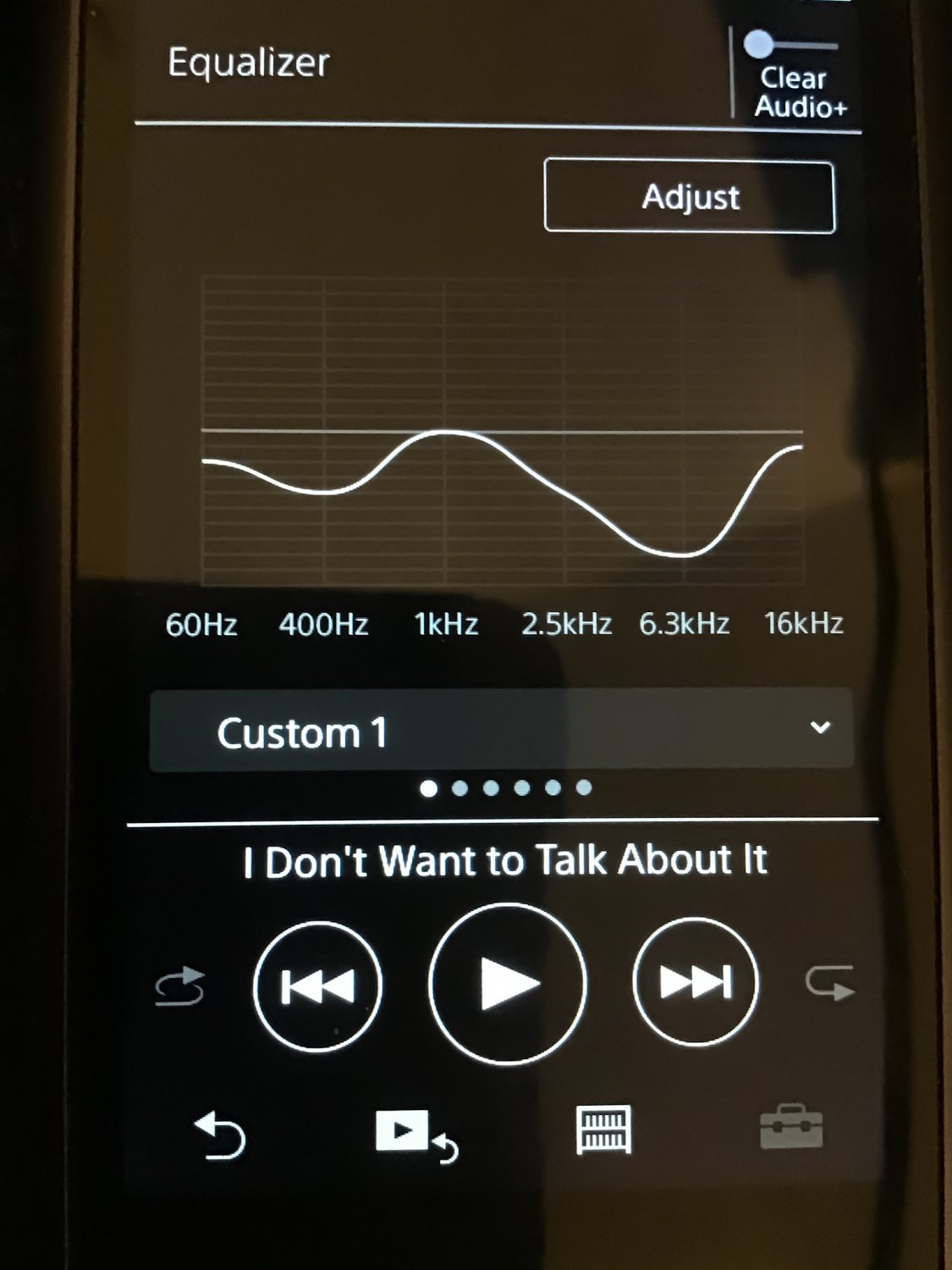
The one in image (Custom 1) is for over-ear headphones, but the saved IEM equalizer setting (Custom 2) looks identical except -2dB @ 60hz.
Last edited:
