Author: our resident expert, DonH50
Here's an attempt to explain aliasing -- the frequency folding that happens whenever you sample a signal. As was discussed in the Sampling 101 thread, whenever you sample a signal at a rate of X samples/sec (X S/s), the highest output signal is < X/2, the Nyquist rate. That is, when sampling at fs, any frequency equal to or greater than fs/2 will be aliased to fall with the frequency band from 0 to < fs/2.
For CD-rate sampling at 44.1 kS/s, we can convert a signal no higher than 22.05 kHz, or aliasing will occur. If the ADC has sufficient bandwidth, it can capture a signal higher than that, but it will be folded back (aliased) into that 0 - 22.05 kHz region. If the ADC is perfect, the amplitude and phase will be unchanged, but the frequency will be reflected about the Nyquist frequency, 22.05 kHz. A picture may help:
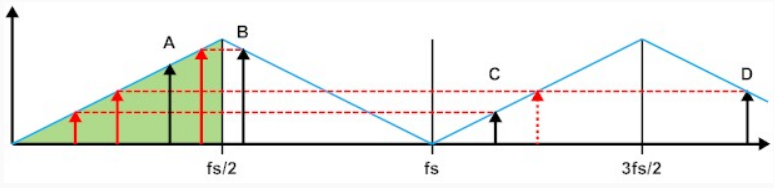
This picture shows a frequency (x) axis with the Nyquist frequency (fs/2), sampling frequency (fs), and third Nyquist frequency (3fs/2) indicated. There are four frequencies, A-D, shown as single tones (black spikes). I have also drawn blue triangles to help us see what happens as frequencies exceed Nyquist.
Signal A is in the first Nyquist band (baseband) and is not affected. If we apply this as an input to an ADC, or output to a DAC, it will come out just as we intended (assuming we have no other errors).
Signal B is just over the first Nyquist frequency and so is aliased back to baseband, as shown by the dotted line and new frequency in red. If we apply this input to an ADC (or DAC), it is folded across the triangle (aliased) back to the first Nyquist band.
Signal C is above the sampling frequency, in the third Nyquist band (third region from the left 0 Hz point). Note the slope of the triangle; we can draw a line from this signal all the way to baseband, where we see a very high frequency appears now as relatively low-frequency output from the ADC (or DAC).
Signal D, up in the fourth Nyquist band, is a little more interesting. Note the slope of the triangle is down instead of up, so we must first reflect it about the 3fs/2 Nyquist point to generate the (dashed red) intermediate signal, and then it is easy to translate to baseband. Think of picking up that high triangle and putting it down on top of the green "good" baseband triangle. Again, a very high signal is converted to a low one as a result.
IF our ADC (or DAC) is perfect and has infinite bandwidth (or at least more than enough for these examples), then the tones above Nyquist are perfectly recreated in baseband except that their original frequency content is lost. To prevent this from happening, and perhaps more importantly to ensure only baseband signals are converted, an anti-alias filter must be placed before the ADC to prevent higher-frequency signals from reaching its input. Any higher-frequency signals that are converted will be aliased to baseband, where we cannot tell if they are part of the music or some noise that got coupled in and converted because the ADC does not know any better.
A special note about DACs is that, although they cannot be fed a signal above Nyquist and properly recreate it, their output can contain higher-frequency content as the output of a DAC is after the sampling point. So, a filter is usually used at a DAC’s output to prevent high-frequency noise from blasting through the rest of the system, which in audio means saving our tweeters!
HTH – Don
Here's an attempt to explain aliasing -- the frequency folding that happens whenever you sample a signal. As was discussed in the Sampling 101 thread, whenever you sample a signal at a rate of X samples/sec (X S/s), the highest output signal is < X/2, the Nyquist rate. That is, when sampling at fs, any frequency equal to or greater than fs/2 will be aliased to fall with the frequency band from 0 to < fs/2.
For CD-rate sampling at 44.1 kS/s, we can convert a signal no higher than 22.05 kHz, or aliasing will occur. If the ADC has sufficient bandwidth, it can capture a signal higher than that, but it will be folded back (aliased) into that 0 - 22.05 kHz region. If the ADC is perfect, the amplitude and phase will be unchanged, but the frequency will be reflected about the Nyquist frequency, 22.05 kHz. A picture may help:
This picture shows a frequency (x) axis with the Nyquist frequency (fs/2), sampling frequency (fs), and third Nyquist frequency (3fs/2) indicated. There are four frequencies, A-D, shown as single tones (black spikes). I have also drawn blue triangles to help us see what happens as frequencies exceed Nyquist.
Signal A is in the first Nyquist band (baseband) and is not affected. If we apply this as an input to an ADC, or output to a DAC, it will come out just as we intended (assuming we have no other errors).
Signal B is just over the first Nyquist frequency and so is aliased back to baseband, as shown by the dotted line and new frequency in red. If we apply this input to an ADC (or DAC), it is folded across the triangle (aliased) back to the first Nyquist band.
Signal C is above the sampling frequency, in the third Nyquist band (third region from the left 0 Hz point). Note the slope of the triangle; we can draw a line from this signal all the way to baseband, where we see a very high frequency appears now as relatively low-frequency output from the ADC (or DAC).
Signal D, up in the fourth Nyquist band, is a little more interesting. Note the slope of the triangle is down instead of up, so we must first reflect it about the 3fs/2 Nyquist point to generate the (dashed red) intermediate signal, and then it is easy to translate to baseband. Think of picking up that high triangle and putting it down on top of the green "good" baseband triangle. Again, a very high signal is converted to a low one as a result.
IF our ADC (or DAC) is perfect and has infinite bandwidth (or at least more than enough for these examples), then the tones above Nyquist are perfectly recreated in baseband except that their original frequency content is lost. To prevent this from happening, and perhaps more importantly to ensure only baseband signals are converted, an anti-alias filter must be placed before the ADC to prevent higher-frequency signals from reaching its input. Any higher-frequency signals that are converted will be aliased to baseband, where we cannot tell if they are part of the music or some noise that got coupled in and converted because the ADC does not know any better.
A special note about DACs is that, although they cannot be fed a signal above Nyquist and properly recreate it, their output can contain higher-frequency content as the output of a DAC is after the sampling point. So, a filter is usually used at a DAC’s output to prevent high-frequency noise from blasting through the rest of the system, which in audio means saving our tweeters!
HTH – Don
