Note: this article was originally written by our DAC/technical expert, @DonH56.
The previous thread on DAC fundamentals provided an overview of conventional (Nyquist) DACs. This thread will introduce oversampling and the delta-sigma architecture that dominates the DACs used in consumer audio gear today.
A few definitions:
Nyquist = fs/2 = 1/2 the sampling frequency. This is the highest frequency that a sampled system can correctly capture and reproduce. Any higher, and the frequency information is lost. Note that Nyquist applies to the highest frequency in the signal, so an audio system can reproduce a 20 kHz sine wave ( a single tone) but not a 20 kHz square wave (which has many higher harmonics). A system sampling at frequency fs, e.g. 40,000 cycles per second (40 kHz), can acquire up to (but not including) 20 kHz signals.
Oversampling refers to how much "extra" bandwidth, or sampling rate, we have relative to the Nyquist rate. For the example above, if we sampled at 80 kHz instead of 40 kHz and kept our desired bandwidth the same (20 kHz), we would be oversampling by two.
SNR = signal-to-noise ratio. The ratio from the signal level, typically at full-scale output, to the total noise level. The noise level is the "sum" (actually, the root-sum-squared, or RSS, value) of all the energy except the signal. While still widely iused, SINAD, signal-to-noise-and distortion, is the parameter of choice now. The problem with SNR is that some people included distrotion terms in the SNR, and some did not, leading to confusion. SINAD includes everything but signal in the "noise" measurement.
"Order" refers to the mathematical order of a system, or system of equations. Without going deeper, a single-pole filter with 6 dB/octave roll-off is a first-order system. A second-order filter has two poles and rolls off at 12 dB/octave. For equations, y = mx is first order in x; y = x^2 is second-order.
<Let me know if more should be added here; I don't want to clutter this too much.>
On to the article...
Recall that a 16-bit Nyquist DAC running at 44.1 kS/s and delivering a 1 kHz signal provided 98 dB signal-to-noise-and-distortion ratio (SINAD; identical to SNR for this ideal DAC since there is no other distortion) and 128 dB spurious-free dynamic range (SFDR, from signal peak to noise floor). These numbers are determined by quantization noise only (all other noise sources are assumed negligible). Now, if we double the sampling rate, the performance (SINAD and SFDR) stays the same (see Figure 1) although the Nyquist bandwidth (0 to Fs/2) has clearly doubled (note the x-axis now extends to 44.1 kHz instead of 22.05 kHz). This is because quantization noise is (theoretically) related only to resolution, not to sampling rate or signal frequency.
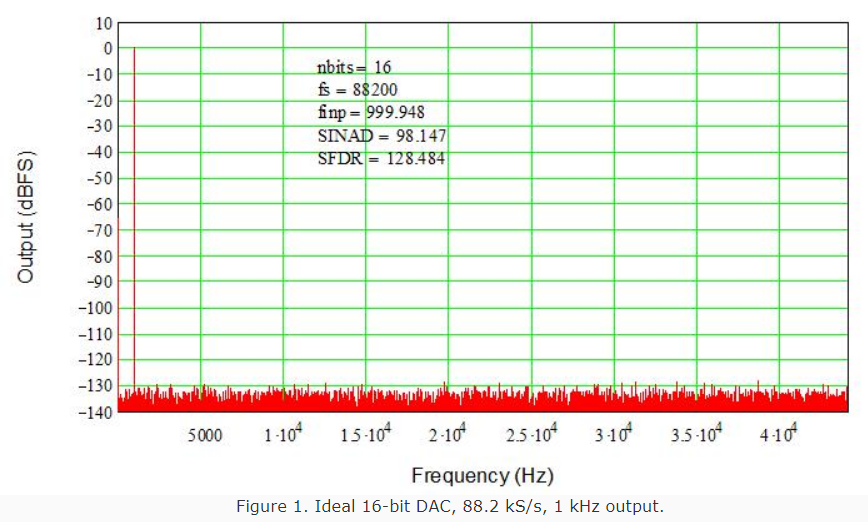
This represents an oversampling ratio of two, i.e. twice the rate needed to produce a 22 kHz maximum output signal. This has some interesting properties worth noting.
Thinking about that last point, if we oversampled by 4, we’d gain 6 dB in SNR and could reduce the resolution by a full bit, getting away with a 15-bit DAC instead of 16 bits for the same noise floor. We could continue to speed up the DAC, reducing its resolution by one bit each time we quadruple the sampling rate. Unfortunately, we don’t save power as doubling the rate also roughly doubles the power while halving the complexity, so power is a wash.
What was needed was a new DAC architecture, one that reduces the number of bits required by more efficiently getting rid of the out-of-band noise. Ideally, this new DAC would also work with modern processing trends that favor digital, not analog, circuits (if you can’t beat them, join them). The architecture that has won (for now, anyway) is based upon delta-sigma modulators, a concept originally developed in the 1930’s for analog communications. Figure 2 shows a simplified first-order delta-sigma (DS) modulator block diagram. An initial difference (delta) cell is followed by a summer (sigma) block and the result applied to a 1-bit DAC. The DAC’s output is fed back to the input. The feedback loop effectively passes the signal while suppressing quantization noise.
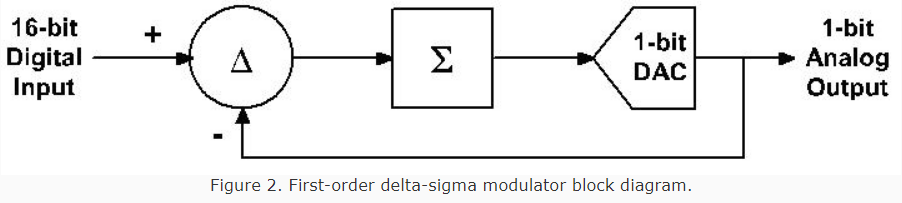
Figure 3 below shows the linearized signal and noise magnitude transfer functions for various delta-sigma loops. The first-order (1o) curves represent the modulator above. At low frequencies, the signal (solid red line) is unity-gain, while the DAC’s quantization noise (dashed red line) is essentially zero. This means the signal goes through the modulator unchanged, but quantization noise is suppressed (approximately zero) at the output. As frequency rises, the signal falls to zero and the noise increases to unity. Higher-order loops provide steeper curves (as evidenced by the other curves -- solid for signal, dashed for noise) that cross higher in frequency, allowing lower oversampling ratios (or wider signal bandwidth for a given sampling rate). Modern DS DACs may use 4th – 6th order modulators.
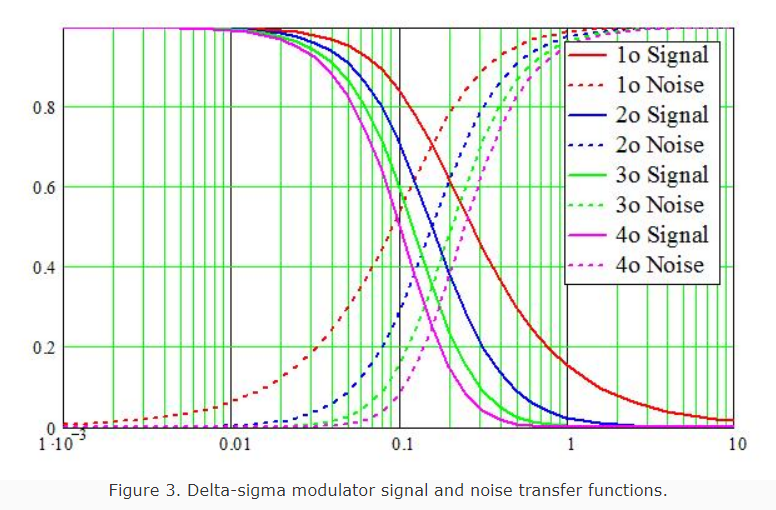
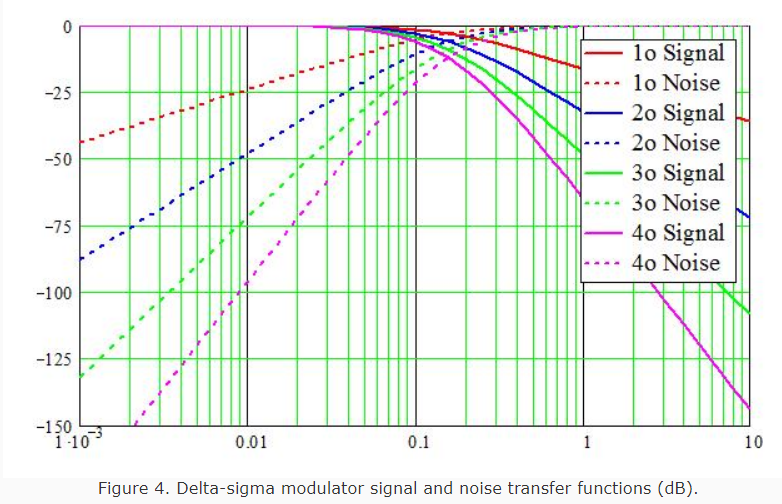
Figure 4 shows the same plot but with amplitude on a log (dB) scale. This better shows the SNR improvement obtained with higher-order loops. While the scale is normalized (and thus does not relate directly to a particular oversampling ratio, OSR), this graph highlights some of the key requirements for high performance. For example, to achieve about 16-bit performance requires a fourth-order modulator operating at ~100x the signal bandwidth (where f = 1 represents the sampling rate -- this is not an exact ratio, but serves to illustrate the point that very high oversampling ratios are needed).
Note that an ideal summer (integrator) has infinite gain at d.c., falling as frequency rises. Delving briefly into equations, if the forward loop gain is A then it is easy to show that the signal and noise transfer functions for the first-order modulator are:
Signal = A/(A+1) --> 1 when A is large
Noise = 1/(A+1) --> 0 when A is large
This accomplishes the desired transfer function, shaping and concentrating the noise into the higher frequencies while keeping the signal gain unity at lower frequencies. And, this performance is achieved with only a single-bit DAC! As a single bit is inherently matched to itself, theoretically perfect linearity is possible. Adding more bits will increase the SNR by 6 dB for each additional bit, but requires precision matching of levels. For example, using a four-bit DAC adds (3 extra bits * 6 dB/bit) = 18 dB additional SNR, but the levels within the 4-bit DAC must be accurate to 16 bits if we desire a 16-bit result. Trimming and digital compensation are used in commercial multi-bit DS DACs to provide the required precision.
For given bandwidth and an L-order modulator, the SNR improves by (6L+3) dB for every doubling of the sampling rate, providing (L+0.5) extra bits resolution. A first-order modulator (L = 1) requires an OSR of about 2048 to achieve 16-bit performance (98 dB SNR), or about 90 MS/s. That is very high for an audio system! A 2nd-order modulator requires about 128x OSR (5.65 MS/s), a much more reasonable value though still high. A 4th-order modulator requires only about 16x OSR, 705.6 kS/s. Clearly, increasing the modulator order substantially reduces the required sampling rate. However, high-order loops are intrinsically unstable, requiring compensation loops that reduce their performance from ideal. In practice higher rates are required due to various non-ideal circuit effects, and multi-bit DACs are often used to provide greater performance (after compensation) without exorbitant sampling rates.
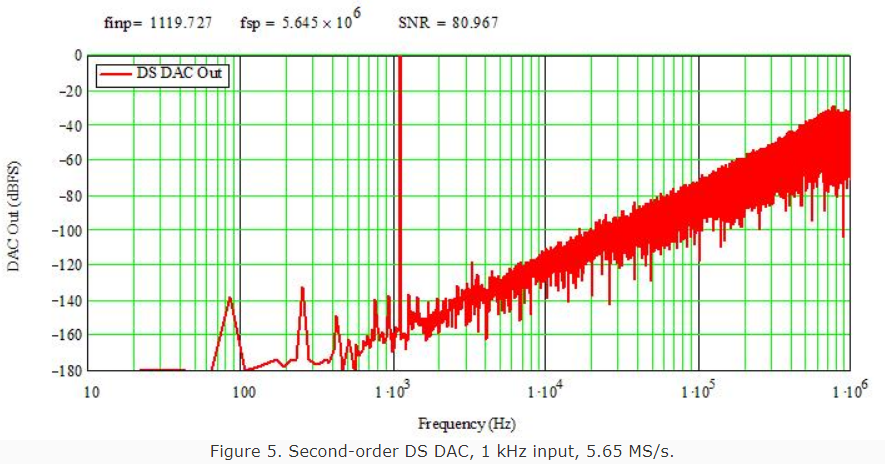
Figure 5 shows the simulated output from a second-order one-bit DS DAC running at 5.65 MS/s with a 1 kHz output. Unlike the linearized curves from the simpler model above, this is for a (model of a) "real" sampled-data system with a 16-bit (ideal) input signal such as your CD player might provide. Note that, while the SFDR is about 100 dB at 20 kHz, the SNR in the audio baseband is only 81 dB. The spurs at very low frequencies are artifacts of the simulation; more points would help reduce those somewhat. However, finite-length digital filters can also introduce low-frequency tones. These arise in part because, without infinite length, some of the digital values repeat periodically, leading to spurs in the frequency domain. However, this simulation clearly shows how a low in-band noise floor can be obtained with very low-resolution DACs by using a delta-sigma modulator to shape the quantization noise into the high-frequency region (out of the audio band). The (one, anyway) trade is a much higher sampling rate.
With sampling rates up in the MHz (millions of cycles per second) region, several decades above the audio band, much lower-order (and thus better-behaved) filters can be used at the output of DS DACs (or, input of DS ADCs). Higher-order modulators in particular have lower noise floor through and past the audio band, and though they rise more rapidly at higher frequencies, the filter corner can be moved to well above the audio band. This minimizes filter issues (phase shift, ringing, amplitude variation, etc.) within the audio band.
I have not yet delved into various error sources and other non-ideal effects, but hopefully this article provides a foundation for understanding how a basic delta-sigma DAC operates and why it is useful.
For further reading (bibliography):
1241-2000: IEEE Standard for Terminology and Test Methods for Analog-To-Digital Converters, IEEE Press, 2001.
J. C. Candy and G. C. Temes, Oversampling Delta-Sigma Data Converters, IEEE Press, 1992.
The previous thread on DAC fundamentals provided an overview of conventional (Nyquist) DACs. This thread will introduce oversampling and the delta-sigma architecture that dominates the DACs used in consumer audio gear today.
A few definitions:
Nyquist = fs/2 = 1/2 the sampling frequency. This is the highest frequency that a sampled system can correctly capture and reproduce. Any higher, and the frequency information is lost. Note that Nyquist applies to the highest frequency in the signal, so an audio system can reproduce a 20 kHz sine wave ( a single tone) but not a 20 kHz square wave (which has many higher harmonics). A system sampling at frequency fs, e.g. 40,000 cycles per second (40 kHz), can acquire up to (but not including) 20 kHz signals.
Oversampling refers to how much "extra" bandwidth, or sampling rate, we have relative to the Nyquist rate. For the example above, if we sampled at 80 kHz instead of 40 kHz and kept our desired bandwidth the same (20 kHz), we would be oversampling by two.
SNR = signal-to-noise ratio. The ratio from the signal level, typically at full-scale output, to the total noise level. The noise level is the "sum" (actually, the root-sum-squared, or RSS, value) of all the energy except the signal. While still widely iused, SINAD, signal-to-noise-and distortion, is the parameter of choice now. The problem with SNR is that some people included distrotion terms in the SNR, and some did not, leading to confusion. SINAD includes everything but signal in the "noise" measurement.
"Order" refers to the mathematical order of a system, or system of equations. Without going deeper, a single-pole filter with 6 dB/octave roll-off is a first-order system. A second-order filter has two poles and rolls off at 12 dB/octave. For equations, y = mx is first order in x; y = x^2 is second-order.
<Let me know if more should be added here; I don't want to clutter this too much.>
On to the article...
Recall that a 16-bit Nyquist DAC running at 44.1 kS/s and delivering a 1 kHz signal provided 98 dB signal-to-noise-and-distortion ratio (SINAD; identical to SNR for this ideal DAC since there is no other distortion) and 128 dB spurious-free dynamic range (SFDR, from signal peak to noise floor). These numbers are determined by quantization noise only (all other noise sources are assumed negligible). Now, if we double the sampling rate, the performance (SINAD and SFDR) stays the same (see Figure 1) although the Nyquist bandwidth (0 to Fs/2) has clearly doubled (note the x-axis now extends to 44.1 kHz instead of 22.05 kHz). This is because quantization noise is (theoretically) related only to resolution, not to sampling rate or signal frequency.
This represents an oversampling ratio of two, i.e. twice the rate needed to produce a 22 kHz maximum output signal. This has some interesting properties worth noting.
- The SFDR and SINAD are the same as for Nyquist rate (sometimes referred to as “1x oversampling”). However, the quantization noise is now spread over twice the bandwidth.
- Since we don’t need the extra bandwidth, we can filter out the noise over 22 kHz, and still provide the same 22 kHz output bandwidth we had before (with the Nyquist-rate DAC).
- Since noise energy goes as the square root of bandwidth, we’ll gain sqrt(2) improvement in SNR, or 3 dB (1/2-bit, recalling we gain 6 dB in SNR for each extra bit).
- Alternatively, we could reduce the resolution of the DAC by 1/2-bit and keep the same SNR we had before.
Thinking about that last point, if we oversampled by 4, we’d gain 6 dB in SNR and could reduce the resolution by a full bit, getting away with a 15-bit DAC instead of 16 bits for the same noise floor. We could continue to speed up the DAC, reducing its resolution by one bit each time we quadruple the sampling rate. Unfortunately, we don’t save power as doubling the rate also roughly doubles the power while halving the complexity, so power is a wash.
What was needed was a new DAC architecture, one that reduces the number of bits required by more efficiently getting rid of the out-of-band noise. Ideally, this new DAC would also work with modern processing trends that favor digital, not analog, circuits (if you can’t beat them, join them). The architecture that has won (for now, anyway) is based upon delta-sigma modulators, a concept originally developed in the 1930’s for analog communications. Figure 2 shows a simplified first-order delta-sigma (DS) modulator block diagram. An initial difference (delta) cell is followed by a summer (sigma) block and the result applied to a 1-bit DAC. The DAC’s output is fed back to the input. The feedback loop effectively passes the signal while suppressing quantization noise.
Figure 3 below shows the linearized signal and noise magnitude transfer functions for various delta-sigma loops. The first-order (1o) curves represent the modulator above. At low frequencies, the signal (solid red line) is unity-gain, while the DAC’s quantization noise (dashed red line) is essentially zero. This means the signal goes through the modulator unchanged, but quantization noise is suppressed (approximately zero) at the output. As frequency rises, the signal falls to zero and the noise increases to unity. Higher-order loops provide steeper curves (as evidenced by the other curves -- solid for signal, dashed for noise) that cross higher in frequency, allowing lower oversampling ratios (or wider signal bandwidth for a given sampling rate). Modern DS DACs may use 4th – 6th order modulators.
Figure 4 shows the same plot but with amplitude on a log (dB) scale. This better shows the SNR improvement obtained with higher-order loops. While the scale is normalized (and thus does not relate directly to a particular oversampling ratio, OSR), this graph highlights some of the key requirements for high performance. For example, to achieve about 16-bit performance requires a fourth-order modulator operating at ~100x the signal bandwidth (where f = 1 represents the sampling rate -- this is not an exact ratio, but serves to illustrate the point that very high oversampling ratios are needed).
Note that an ideal summer (integrator) has infinite gain at d.c., falling as frequency rises. Delving briefly into equations, if the forward loop gain is A then it is easy to show that the signal and noise transfer functions for the first-order modulator are:
Signal = A/(A+1) --> 1 when A is large
Noise = 1/(A+1) --> 0 when A is large
This accomplishes the desired transfer function, shaping and concentrating the noise into the higher frequencies while keeping the signal gain unity at lower frequencies. And, this performance is achieved with only a single-bit DAC! As a single bit is inherently matched to itself, theoretically perfect linearity is possible. Adding more bits will increase the SNR by 6 dB for each additional bit, but requires precision matching of levels. For example, using a four-bit DAC adds (3 extra bits * 6 dB/bit) = 18 dB additional SNR, but the levels within the 4-bit DAC must be accurate to 16 bits if we desire a 16-bit result. Trimming and digital compensation are used in commercial multi-bit DS DACs to provide the required precision.
For given bandwidth and an L-order modulator, the SNR improves by (6L+3) dB for every doubling of the sampling rate, providing (L+0.5) extra bits resolution. A first-order modulator (L = 1) requires an OSR of about 2048 to achieve 16-bit performance (98 dB SNR), or about 90 MS/s. That is very high for an audio system! A 2nd-order modulator requires about 128x OSR (5.65 MS/s), a much more reasonable value though still high. A 4th-order modulator requires only about 16x OSR, 705.6 kS/s. Clearly, increasing the modulator order substantially reduces the required sampling rate. However, high-order loops are intrinsically unstable, requiring compensation loops that reduce their performance from ideal. In practice higher rates are required due to various non-ideal circuit effects, and multi-bit DACs are often used to provide greater performance (after compensation) without exorbitant sampling rates.
Figure 5 shows the simulated output from a second-order one-bit DS DAC running at 5.65 MS/s with a 1 kHz output. Unlike the linearized curves from the simpler model above, this is for a (model of a) "real" sampled-data system with a 16-bit (ideal) input signal such as your CD player might provide. Note that, while the SFDR is about 100 dB at 20 kHz, the SNR in the audio baseband is only 81 dB. The spurs at very low frequencies are artifacts of the simulation; more points would help reduce those somewhat. However, finite-length digital filters can also introduce low-frequency tones. These arise in part because, without infinite length, some of the digital values repeat periodically, leading to spurs in the frequency domain. However, this simulation clearly shows how a low in-band noise floor can be obtained with very low-resolution DACs by using a delta-sigma modulator to shape the quantization noise into the high-frequency region (out of the audio band). The (one, anyway) trade is a much higher sampling rate.
With sampling rates up in the MHz (millions of cycles per second) region, several decades above the audio band, much lower-order (and thus better-behaved) filters can be used at the output of DS DACs (or, input of DS ADCs). Higher-order modulators in particular have lower noise floor through and past the audio band, and though they rise more rapidly at higher frequencies, the filter corner can be moved to well above the audio band. This minimizes filter issues (phase shift, ringing, amplitude variation, etc.) within the audio band.
I have not yet delved into various error sources and other non-ideal effects, but hopefully this article provides a foundation for understanding how a basic delta-sigma DAC operates and why it is useful.
For further reading (bibliography):
1241-2000: IEEE Standard for Terminology and Test Methods for Analog-To-Digital Converters, IEEE Press, 2001.
J. C. Candy and G. C. Temes, Oversampling Delta-Sigma Data Converters, IEEE Press, 1992.
Last edited:


