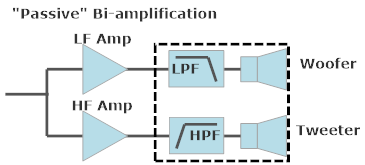
This article provides a quick look at how bi-amplification works. The conventional scheme is to split the signal into two frequency bands before the power amplifiers that drive the speakers. The bass (LF) amp sees only LF signals and drives only the LF driver (woofer). The treble (HF) amp sees only HF signals and drives only the HF driver. This reduces the signal for each amplifier, improving headroom and potentially allowing amplifiers to be chosen for their target frequency range without the burden of supplying the full-range audio signal.
Here is a regular single-amplifier system and passive speaker crossover. The crossover comprises a low-pass filter (LPF) for the woofer and high-pass filter (HPF) for the tweeter. The crossover is inside the speaker; the dashed outline shows there can be a single or split (high/low) set of speaker input terminals, but the connection is the same as far as the amplifier is concerned.
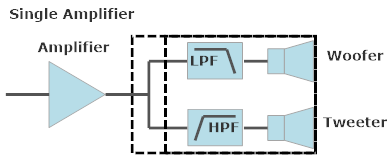
For this experiment both crossovers are second-order (12 dB/octave) Linkwitz-Riley designs and the same whether passive or active. The crossover frequency is 1 kHz. The speakers are represented by 8-ohm resistors in this simplified analysis. This is the transfer function (frequency response) of the crossover:
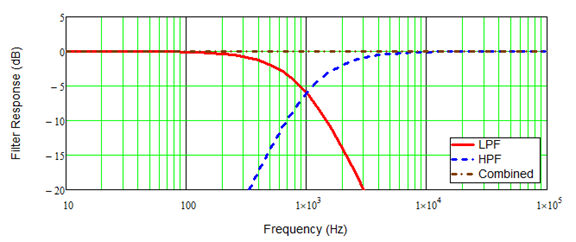
For analysis I am using two signals at 300 Hz (LF) and 3 kHz (HF) which on a log scale sit on either side of the crossover:
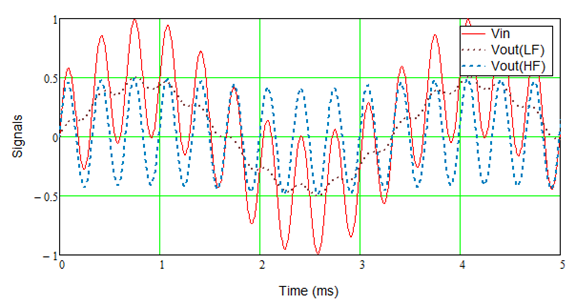
The output voltage from the amplifier includes both signals, of course:
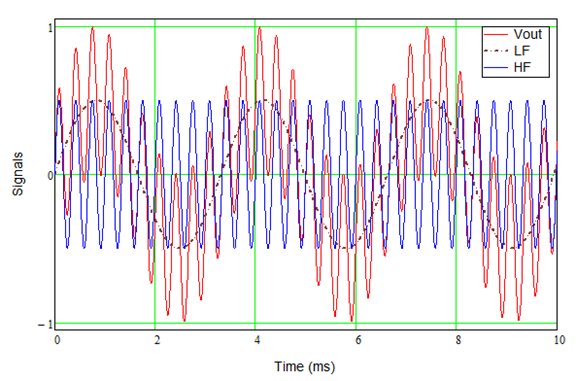
You can see how the low-frequency signal and high-frequency combine to create the modulated output signal. Since both signals have the same amplitude, the combined signal is twice the level of the individual signals. While this makes it easy to see, note in practice HF signals are typically much lower in amplitude than the LF signals (see Equal Loudness Curves in Wikipedia or wherever).
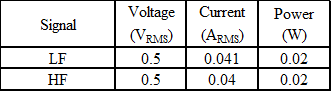
The relative voltage, current, and power is in the table below. The numbers are low since I am using a small signal; everything is relative. The combined RMS voltage for this case is simply sqrt(LF^2 + HF^2). The power is the average power, the product of RMS voltage and current (RMS power is a meaningless term though often used mistakenly).

Now repeat the experiment, but place a line-level crossover before the power amps. The crossover is typically active but could be passive; the usurpation of the term “passive bi-amplification” the way AVR marketing defines it is an on-going source of confusion.
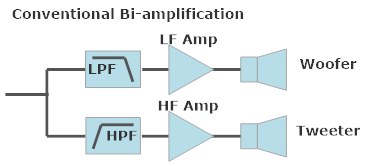
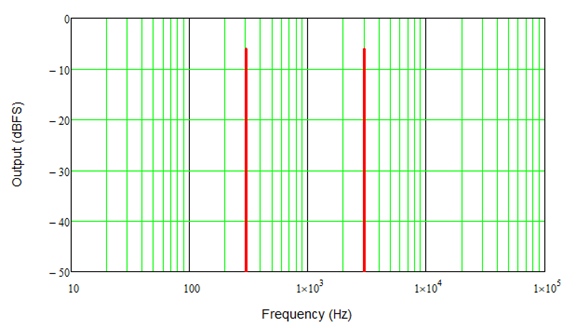
There are now two amplifiers but each only handles a portion of the signal divided into two (low and high) frequency bands. Since the crossover is not ideal, that is does not drop instantly to zero on either side of the crossover frequency, a little bit of the HF signal is still seen in the LF output and vice-versa. It is a little hard to see in the time-domain plot, but the frequency-domain plots clearly show this.
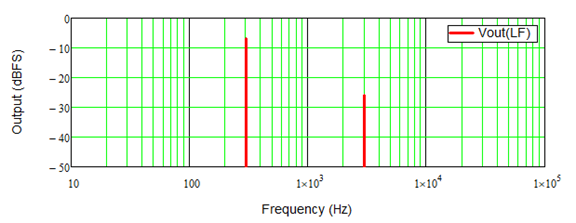
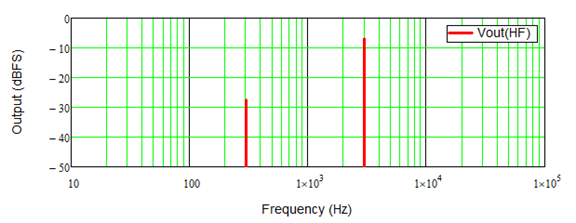
Now we can create a new table showing the parameters of each amplifier in the bi-amplified case:
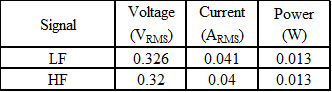
The voltages are similar to the previous table except now they are at the output of the amplifiers and, with the filters, the RMS value is a little lower. The RMS current is reduced more significantly since the load is split between the two amplifiers, and power is also significantly reduced (by about 60%). Note power is not a linear function, but rather the product of voltage and current (a nonlinear function), so splitting the signal this way does not reduce the power by exactly one-half (it is better than that). You could use two amplifiers each one-half the rated power if the single amplifier and deliver the same power to the speaker. The amplifiers also directly drive the speakers so there is no crossover loss, and no chance of the signal from one speaker modulating the other through the crossover circuit, potentially reducing distortion.
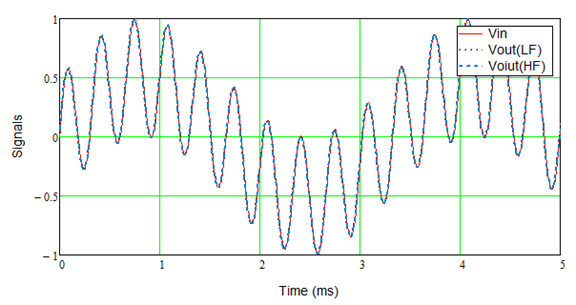
Now consider “passive” bi-amping as implanted by most AVRs and shown below. In this scenario both amplifiers are driven by the same signal, so their outputs have exactly the same voltage. There is no benefit in voltage and, since most amplifiers are essentially voltage-mode designs, no increase in system headroom. Current is reduced from each amplifier, since the passive crossover in the speaker “blocks” current that is out of band, and there is a corresponding reduction in power (not as much as when an active crossover is used, however).
The voltage output of each amplifier is the same:
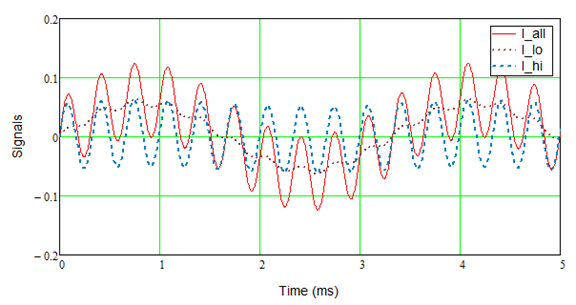
The current is lower since the load seen by each amplifier is only part of the speaker. The LF amp has almost no HF current in its output, and similarly the HF amp has little LF current, even though the voltage is the same.
Here is the parameter table for the “passive” bi-amping case:
And a comparison of all three examples:
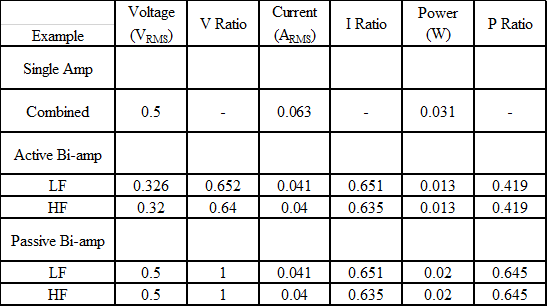
A ratio less than one represents an advantage (decrease) in the parameter the amplifier is delivering to the speaker. In a conventional active bi-amp system, each amplifier delivers only 65% of the voltage and current and only 42% the power of a single amplifier providing the same signal to the speakers. A “passive” bi-amp system the way an AVR does it has no voltage benefit but does require less current from each amplifier, resulting in the same 65% reduction in current, but due to the higher voltage must deliver 65% of the power. A reduction, true, but less dramatic than for an active bi-amp system, and since there is no reduction in the voltage that must be delivered there is no (voltage) headroom advantage. Where an active system would allow you to replace a 200 W amplifier with two 100 W amplifiers, the passive scheme requires two 200 W amplifiers to maintain the voltage headroom required.
One other significant consideration is how we hear as reflected in the equal-loudness curves (see e.g. https://en.wikipedia.org/wiki/Equal-loudness_contour). It take much higher levels of low-frequency signals to sound as loud as midrange signals. At 80 dB SPL, a 100 Hz signal must be about 10 dB louder (10x the power) to sound as loud as a 1 kHz signal, and must be about 20 dB louder (100x the power) by around 60 Hz. That is one reason bi-amplified systems (of the non-passive kind) often use a much larger bass amplifier than for the tweeter.
A few key points about “passive” bi-amping, from the original version of this roughly ten years ago:
FWIWFM - Don
Here is a regular single-amplifier system and passive speaker crossover. The crossover comprises a low-pass filter (LPF) for the woofer and high-pass filter (HPF) for the tweeter. The crossover is inside the speaker; the dashed outline shows there can be a single or split (high/low) set of speaker input terminals, but the connection is the same as far as the amplifier is concerned.
For this experiment both crossovers are second-order (12 dB/octave) Linkwitz-Riley designs and the same whether passive or active. The crossover frequency is 1 kHz. The speakers are represented by 8-ohm resistors in this simplified analysis. This is the transfer function (frequency response) of the crossover:
For analysis I am using two signals at 300 Hz (LF) and 3 kHz (HF) which on a log scale sit on either side of the crossover:
The output voltage from the amplifier includes both signals, of course:
You can see how the low-frequency signal and high-frequency combine to create the modulated output signal. Since both signals have the same amplitude, the combined signal is twice the level of the individual signals. While this makes it easy to see, note in practice HF signals are typically much lower in amplitude than the LF signals (see Equal Loudness Curves in Wikipedia or wherever).
The relative voltage, current, and power is in the table below. The numbers are low since I am using a small signal; everything is relative. The combined RMS voltage for this case is simply sqrt(LF^2 + HF^2). The power is the average power, the product of RMS voltage and current (RMS power is a meaningless term though often used mistakenly).
Now repeat the experiment, but place a line-level crossover before the power amps. The crossover is typically active but could be passive; the usurpation of the term “passive bi-amplification” the way AVR marketing defines it is an on-going source of confusion.
There are now two amplifiers but each only handles a portion of the signal divided into two (low and high) frequency bands. Since the crossover is not ideal, that is does not drop instantly to zero on either side of the crossover frequency, a little bit of the HF signal is still seen in the LF output and vice-versa. It is a little hard to see in the time-domain plot, but the frequency-domain plots clearly show this.
Now we can create a new table showing the parameters of each amplifier in the bi-amplified case:
The voltages are similar to the previous table except now they are at the output of the amplifiers and, with the filters, the RMS value is a little lower. The RMS current is reduced more significantly since the load is split between the two amplifiers, and power is also significantly reduced (by about 60%). Note power is not a linear function, but rather the product of voltage and current (a nonlinear function), so splitting the signal this way does not reduce the power by exactly one-half (it is better than that). You could use two amplifiers each one-half the rated power if the single amplifier and deliver the same power to the speaker. The amplifiers also directly drive the speakers so there is no crossover loss, and no chance of the signal from one speaker modulating the other through the crossover circuit, potentially reducing distortion.
Now consider “passive” bi-amping as implanted by most AVRs and shown below. In this scenario both amplifiers are driven by the same signal, so their outputs have exactly the same voltage. There is no benefit in voltage and, since most amplifiers are essentially voltage-mode designs, no increase in system headroom. Current is reduced from each amplifier, since the passive crossover in the speaker “blocks” current that is out of band, and there is a corresponding reduction in power (not as much as when an active crossover is used, however).
The voltage output of each amplifier is the same:
The current is lower since the load seen by each amplifier is only part of the speaker. The LF amp has almost no HF current in its output, and similarly the HF amp has little LF current, even though the voltage is the same.
Here is the parameter table for the “passive” bi-amping case:
And a comparison of all three examples:
A ratio less than one represents an advantage (decrease) in the parameter the amplifier is delivering to the speaker. In a conventional active bi-amp system, each amplifier delivers only 65% of the voltage and current and only 42% the power of a single amplifier providing the same signal to the speakers. A “passive” bi-amp system the way an AVR does it has no voltage benefit but does require less current from each amplifier, resulting in the same 65% reduction in current, but due to the higher voltage must deliver 65% of the power. A reduction, true, but less dramatic than for an active bi-amp system, and since there is no reduction in the voltage that must be delivered there is no (voltage) headroom advantage. Where an active system would allow you to replace a 200 W amplifier with two 100 W amplifiers, the passive scheme requires two 200 W amplifiers to maintain the voltage headroom required.
One other significant consideration is how we hear as reflected in the equal-loudness curves (see e.g. https://en.wikipedia.org/wiki/Equal-loudness_contour). It take much higher levels of low-frequency signals to sound as loud as midrange signals. At 80 dB SPL, a 100 Hz signal must be about 10 dB louder (10x the power) to sound as loud as a 1 kHz signal, and must be about 20 dB louder (100x the power) by around 60 Hz. That is one reason bi-amplified systems (of the non-passive kind) often use a much larger bass amplifier than for the tweeter.
A few key points about “passive” bi-amping, from the original version of this roughly ten years ago:
- Each amplifier requires the same voltage output as a single amplifier since they each have the same signal. There is no voltage headroom benefit.
- Because the speaker load is essentially an “open” in the unused frequency band, less current output is required from each amp.
- There is no net system power increase at the speakers assuming the amps have the same voltage rails (e.g. inside an AVR or multichannel amplifier with the same power voltage rails to all amps). If you had a 100 W amp before, and bi-amp with two 100 W amplifiers, passive bi-amping does not give you 200 W to the speaker. You have split the load into two frequency bands, but the maximum power is the same to the speaker. That is, 100 W to the lows and 100 W to the highs is the same as having a 100 W amp that covers the entire frequency range. It is not the same as driving the speaker with a 200 W amplifier; to increase the power, you need to increase the voltage rails. There is not an effective increase in power headroom as there is for an active approach.
- In fact, there is more power lost, since the amps are not 100% efficient. That is, it actually take more energy from the power supply to passively bi-amp than if you used a single amp. This is also true for active bi-amping, but in that case we can choose lower-power amps for the highs (which rarely need the same power as the lows) and realize net power savings. That does not happen with (typical) passive bi-amping.
- There is no damping factor improvement over a single amp since the speaker crossovers are still in-circuit. One of the benefits of active bi-amping is direct connection from amp to driver, providing better driver control; this is not true in passive bi-amping.
- There is no longer electrical interaction among drivers with passive (or active) bi-amping. (There may still be mechanical coupling if the drivers are not isolated from each other.) That is, if the woofer starts to distort the input signal through electromechanical forces, it no longer modulates the HF amp’s output. One plus for bi-amping, active or passive.
- If the amps share a power supply, as do most AVRs and many (most?) multichannel amps, then modulation between high and low amps can still occur through the power supply. This can also happen with active bi-amping, although separate amps are the norm in the pro world. At least when I have done it…
- There may be some distortion reduction since power output is lessened in the amps. I suspect this is not significant, but it should happen due to the lower current draw. The catch is that the voltage swing of each amp is unchanged, so any distortion related to voltage swing is not changed. Only distortion components depending on output current may be reduced. That is design-dependent, but since most amps are primarily voltage-mode amps, I suspect any distortion reduction is small.
- You have two amps now so presumably noise is a little higher since you have two uncorrelated noise sources. At the speaker outputs I suspect it’s a wash since only a reduced frequency band gets through the drivers to hear.
- Thermally it is a loss since no amp is 100% efficient. There is always a little “waste” power that gets turned into heat, both standing bias current (especially if not class D amps) and losses through the components in the amp. Thus passive bi-amping will cause your AVR/amp to run hotter than if using a single amp (assuming unused channels). It is worth noting that amplifiers are typically most efficient at maximum output; the HF amp is probably loafing most of the time and thus wasting power and generating heat.
FWIWFM - Don
Last edited:
