EDIT: Kind translation to Spanish by member @RamiroColasurdo here: https://www.audiosciencereview.com/...-audio-measurements.10523/page-8#post-1486638
A detailed tutorial on how one can characterize the true performance of DACs (whether stand-alone or part of your AVR or A/V processor).
Without any formal training, most of us understand basic analog measurements such as frequency response. The concepts there are intuitive: any deviation from flat amplitude at any frequency shows an anomaly. Step into digital audio such as Digital To Analog Converters (DAC) the game becomes much more complex, spanning many domains of audio from signal processing to psychoacoustics. Do you know what dBFS is? How about composition of a square wave?
You might think digital audio is “perfect” and hence there is no need to measure such devices. That is not the case. While digital data is there forever, the moment you convert it to sound, it is an analog voltage that is ideally accurate to 24 bits. Turns out this is impossible in real life but many DACs fall way short of what can be done. Some DACs even fail to get to 16 bits let alone 24 bits.
Many DAC manufacturers use off-the-shelf DAC chips from the same few silicon providers. Alas, two DAC implementations using identical DAC chips can have very different performance. Sadly, price, brand reputation, designer behind the product, glowing reviews and market adoption do not predict performance. I have tested over 120 DACs so far [now over 220] and the results are all over the place. Some no name low ost DACs have exceptional performance. Others from very well-respected companies retailing for thousands of dollars fail miserably when measured the same way.
To give you a sense of how varied the performance of DACs are, take a look at Figure 1. This is an ordered ranking of “SINAD” ratings for 118 DACs. SINAD is the ratio of signal over noise summed with distortion. The higher the SINAD, the lower the amount of noise and distortion. The range of SINADs in the test DACs in Figure 1 is an incredible 55 dB to 118! Remember, dB is a logarithmic scale so even small differences can be significant.

Figure 1: SINAD (distortion & noise) rating of a range of products tested at AudioScienceReview.com
Since there are product variations and test conditions that vary somewhat, I don’t suggest readers look too closely at the SINAD numbers. Instead, go by what “bucket” they fall in based on color-coding. For best performance you want products in the blue bucket and avoid those in red.
We are getting ahead of ourselves though. Let’s dig into what such measurements mean and how to evaluate them.
Instrumentation
Audio measurements are performed using specialized instruments for this purpose. While you can perform some of these measurements using a good audio interface/sound card (ADC) and appropriate software, I have yet to find a combination that replicates the same as what can be done with dedicated audio measurement hardware. These devices run in a “closed loop.” meaning they can change one or two parameters, measure the output of the DAC, and then iterate. This gives us data across a range of operating points which can uncover issues that are not visible with “static” measurements.
The leader in audio instrumentation is Audio Precision. Their analyzers transformed the audio measurement industry back in 1990s and they have continued to maintain their lead until today. Using them means that there is a good chance someone else has access to them and can replicate the measurements. Unfortunately these analyzers are not cheap. The APx555 model that I use has a retail price of $28,000.
There are lower cost models (from other manufacturers such as Prism Sound) but you give up performance. In the context of measuring state-of-the-art DACs, we need to make sure the analyzer’s own distortion and noise are negligible compared to what is being measured. To give you an idea, the APx555 will score above 120 in the SINAD test in Figure 1. It gets there using fancy signal processing and use of two Analog to Digital Converts (ADCs) in parallel. The APx555 is essentially distortionless.
A number of (good) manufactures include measurements from Audio Precision although some are from the older “2700” series system. So learning how the Audio Precision measurements work in this article, will help you understand those specifications too. Of note, the vast majority of companies who provide such detailed graphs perform well and get high praise from me in my reviews. Lack of measurements graphs usually means the company either never measured the device or don’t feel like the measurements provide a positive image of the product. Both are bad news if you are a consumer.
The Dashboard
The APx555 has a real-time mode where the analyzer is constantly measuring the performance of a device. I have configured that so that in a single snapshot, we get a good idea of how well a DAC is performing. I have coined this the “dashboard” and you can see a sample of it in Figure 2. This is a high-performance multi-channel DAC from a small European company called “Okto Research.”
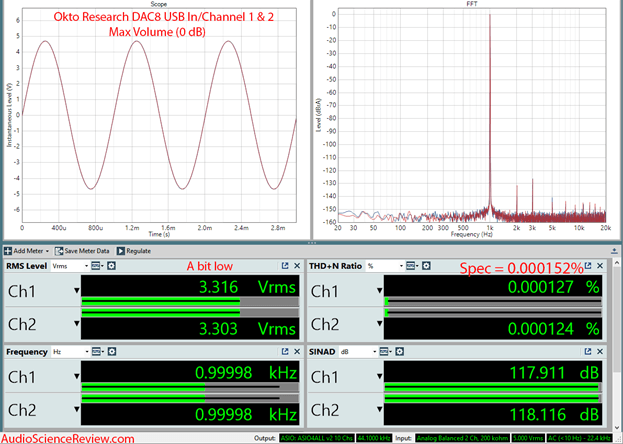
Figure 2: Dashboard view of Okto Research DAC8
This is a USB DAC and the APx555 Audio Precision analyzer is controlling it using that interface. You can tell this in the footnote in green with the term “ASIO.” ASIO is an audio driver interface that the APx555 uses to talk to the USB DAC (it unfortunately does not support any other interface as of this writing). If I were using S/PDIF or Optical interfaces to communicate with the DAC, those would show up instead.
Next to the output interface we see 44100 which is the sampling rate selected. 44100 is the sampling rate for CD and almost all streaming audio services. This can easily be changed and I do that for other tests (e.g. jitter). Since CD-based, 44.1 kHz sampling is so popular, it makes sense to focus on that in our dashboard.
The next text in green says the select input is Analog Balanced and that is exactly what it is. The Okto Research DAC8 only has XLR balanced outputs so that is what I am measuring. If I were testing RCA connections, it would say “unbalanced” there instead.
“200 Kohm” is the input impedance of the Audio Precision analyzer when testing XLR balanced connections. This is a very high impedance meaning the analyzer essentially puts no load on the output of the DAC and usually represents the best performance it can produce. If you have a pre-amp with very low input impedance, you may face issues not represented here although such devices tend to be very rare.
Next bit of text is not important (“5.000 Vrms”). That just says what the scale in the top left pane is. So ignore that.
The last text in the status line is very important as it shows the measurement bandwidth. Even though the APx555 analyzer is designed for audio, it can measure well outside of our hearing range to 1 Megahertz. I use such wide bandwidth when testing class D amplifiers as they create switching noise in hundreds of kilohertz. For DACs in the Dashboard view, I limit the bandwidth to 22.4 kHz, which is just above normal hearing range. And that is what you see in that text for the upper bound.
The lower band says “AC (< 10 Hz)” means that we are NOT measuring down to DC (0 Hz). A DC offset can upset the measurement system so unless there is a good reason for it (e.g. measuring frequency response), I use the “AC” measurement filter that ignores extremely low frequencies below 10 Hz.
The above are the test parameters. Everything else is analysis of what is coming out of the DAC. Let’s dig into those.
On top left we see a waveform. The digital generator in APx555 has been set to output a 1 kHz tone and that is what we see in that waveform display. The sample depth is 24 bits, so we have extreme accuracy here. The DAC takes these “perfect” digital samples and generates an analog waveform from it. That is what we are looking at in the top left. I call this the “time domain” display to contrast it from the FFT, which is the frequency domain of the same signal (explained later).
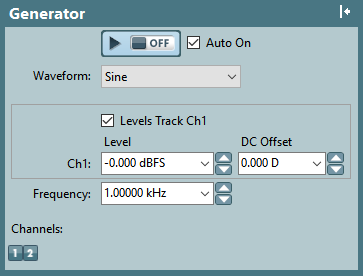
Figure 3: Audio Precision APx555 digital audio generator panel.
I have shown the digital frequency generator panel in APx555 in Figure 3. As you see, I can set the Frequency to whatever I want. 1 kHz is the industry norm for a lot of measurements so that is what I am using in this dashboard view.
The “level” or amplitude of the signal has a funny scale: dBFS. This stands for decibels (dB) from Full Scale. In digital domain, there is no concept of voltages. Everything is just a number. So we rely on a relative, logarithmic scale. 0 dBFS is full amplitude within the format we have set (24-bit PCM). Since this is a dB scale, every reduction of the dBFS by 6 dB represents halving the analog output voltage of the DAC.
You often read in my reviews that so and so dB value is so many bits. We can convert dB to equivalent number of bits (ENOB) by simply dividing the dB value by 6 (this is a bit of approximation). So if I set the digital generator to -120 dBFS (remember 0 dBFS is maximum so all allowable numbers are negative or less than max), it means I am telling the DAC to reproduce a voltage that is represented by 120/6 = 20 bits. If I set it to -96 dBFS then I am asking the DAC to output a level closest to what 16-bit audio samples would represent (16 * 6 = 96 dB).
For the dashboard as shown, the test is usually at 0 dBFS. I say usually because when measuring RCA/unbalanced output we like to see a nominal voltage output from DAC of around 2 volts. Anything less would mean that the DAC may not have enough output to drive your amplifier to max power levels depending on its sensitivity. For the balanced XLR output, this doubles to 4 volts. In our sample dashboard we see 3.1316 volts (RMS), which is too low. The company in question has taken this feedback and plans to release products at 4 volts.
If the DAC output voltage is higher than these nominal values, I often reduce the dBFS incrementally to get it down to where they should be. This sometimes reduces the distortion levels and improves SINAD. Sometimes it doesn’t make a difference.
The next “meter” is on the bottom left and represents the measured frequency from the output of the DAC. Recall that we told our DAC to produce a 1 kHz tone. What we see coming from the DAC is a bit off at 0.99998 kHz. The reason for this is that all DACs have a local clock that has some accuracy error. In this case, it is running a hair slow. This is why if you put two DACs playing side by side, they can drift away from each other over time. This field is informative and usually doesn’t show an issue.
Now let’s focus on the all-important “FFT” window on top right. That is a mathematical conversion of the waveform to the left (the sine wave) into its fundamental components in frequency domain. We think that we told the DAC to produce a 1 kHz tone and that is exactly what it has done. That assumes a perfect DAC that is perfectly linear meaning it produces outputs with infinite accuracy to what is being input. All DACs have conversion errors which create non-linearity. This means that a single sine wave going in, will result in that sine wave coming out plus harmonic distortion (multiples of the source frequency). In addition to harmonic distortion, we also have noise and often spurious tones mixed in that are unrelated to what we asked the DAC to do.
Because the non-linearities in audio are quite small relative to the main signal (a 1 kHz tone in this case), we cannot see them in the sine wave in top right (time domain signal). Conversion to frequency domain nicely takes apart the output of the DAC into subcomponents showing every distortion and spurious tone with ease.
The dashboard view shows that the DAC being measured has a second harmonic (2 kHz) at below -130 dB (1 kHz signal has been set to 0 dB). Translating this into bit depth, the second harmonic distortion is below 21 bits of resolution. This is well below an audible level as our best-case hearing has dynamic range of 116 dB. In that regard, even the taller third harmonic at -128 dB or so is by far below audibility levels. In other words, this DAC is objectively and provably transparent to our hearing when it comes to distortion.
When creating FFT displays, we tell the system how many audio samples to use. In the case of the dashboard, this is set to 32000, which gives very good resolution to see distortion spikes. We can increase this number to over 1 million in APx555. I use 256,000 when showing a dedicated 1 kHz FFT spectrum as seen in Figure 4. The DAC in this test has much so we see a “spray” (series) of distortion spikes, which are worse in the blue channel.
For this measurement, I have set the maximum frequency much higher allowing us to see what is above our hearing range of 20 kHz. We see a few “spurs” (spurious tones) between 45 kHz and 50 kHz. While not audible, good engineering means that the DAC would not spit out such unwanted frequencies.
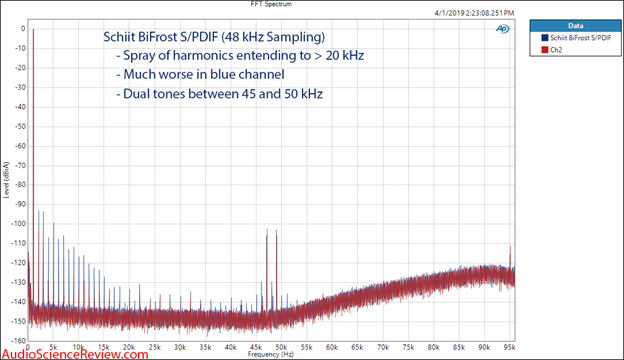
Figure 4: FFT spectrum of distortion and noise in a DAC.
Let’s go back to our dashboard and look at the THD+N Ratio meter. This is a single figure of merit for audio gear that has been around forever. The measurement was performed by playing a 1 kHz tone, capturing that output, and filtering out the 1 kHz with a very narrow notch filter. Anything that remains is either distortion or noise. Sum them all and you get THD+N. With our modern instrumentation we can choose any frequency for testing but since the tradition is 1 kHz, I have stayed with that in the dashboard.
Important note: you may be tempted to read the DAC noise level from the noisy part of the graph/floor in the FFT. DO NOT DO THIS! The true noise floor of a DAC is much higher. When we perform FFT, the more points we use, the lower the noise floor becomes. This is called “FFT gain” and is a good thing as it allows us to see distortion products that may be well buried inside the noise floor of the DAC (and ADC in the measurement gear). The gain can be as much as 30 dB to 40 dB lower than reality! Math can be used to back out this gain using the number of points.
Instead of doing that, we can measure the sum of distortions+noise in the form of THD+N (Total Harmonic Distortion + Noise). This is what is shown in our THD+N Ratio meter below the FFT. THD+N is a very common figure of merit quoted in many product specs.
Below THD+N is the SINAD figure I referenced earlier. SINAD is actually the same value as THD+N but expressed in dB relative to the signal amplitude. This is good because we can, at a glance, compare the SINAD to our hearing dynamic range of 116 dB and know if we are better or worse than it. This is a back of an envelope computation for audibility so don’t completely run with it. Use it as a first order approximation. If a DAC has better SINAD than 116 dB, then we have very high confidence of transparency. If the SINAD is below 116 dB, then the nature of the distortion spectrum will tell us if the distortion is audible or not (i.e. we have to look at the FFT).
THD+N Versus Frequency
Our dashboard view is a performance snapshot at 1 kHz. Performance of devices in general varies as source frequency changes. It is very easy to create such a “sweep” in APx555, having it vary the digital generator source frequency and measuring the THD+N at that point from the output of the DAC. You can see this in Figure 5.
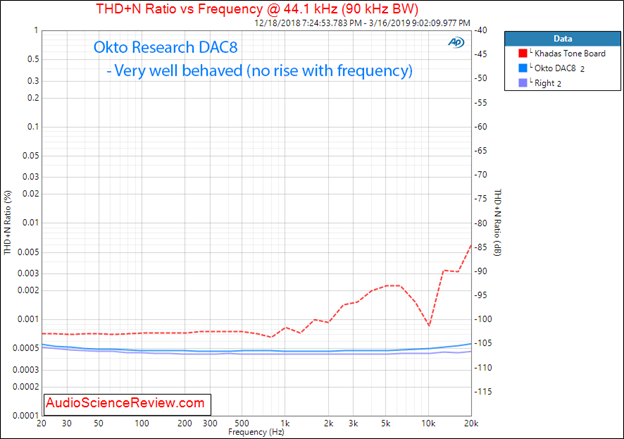
Figure 5: THD+N (distortion+noise) versus Source Frequency.
Note that the measurement in Figure 5 has a bandwidth of 90 kHz unlike the dashboard, which uses 22.4 kHz. Why so much higher? Harmonics are multiples of a frequency. In the dashboard, we use a 1 kHz tone so its multiples all the way to 22 kHz can be captured in 22.4 kHz of bandwidth. Here we are going up to 20 kHz in source frequency so if we stop at just 22.4 kHz, just as well, we won’t capture any harmonic distortion as the second harmonic is at 40 kHz. By using 90 kHz bandwidth we are able to capture up to a fourth harmonic of 20 kHz, which measures most of the distortion we are going to see.
Alas, the higher bandwidth of 90 kHz means that we not only capture harmonic distortion but also any ultrasonic noise and spurious tones. We can see this once again in Figure 6 if we measure the Schiit BiFrost DAC.
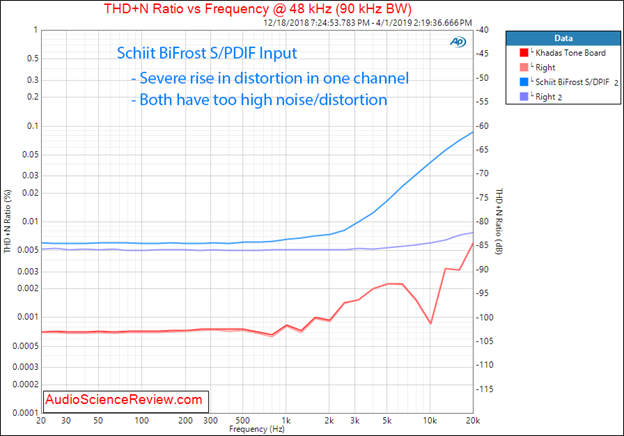
Figure 6: THD+N versus frequency for a lower performing DAC.
The rise in THD+N in one channel is most likely due to unwanted ultrasonic tones than actual harmonic distortion. Notice how much worse that graph in blue is compared to the DAC in red which is a low-cost ($99) bare board DAC (“Khadas Tone Board”).
The most important lesson is that every THD+N graph or specification must include the bandwidth used for measurement. Otherwise the data cannot be interpreted.
Note that some manufactures and reviewers use “a-weighting” when stating THD+N. This is a standardized filter that equalizes the output of the DAC to have less amplitude at low and high frequencies. This is said to better match our hearing. Alas the graph is a too simplistic view of our hearing so I don’t use it. In almost all cases, a-weighting reduces the THD+N so it is popular with manufacturers.
Jitter and Noise
Most audiophiles have heard of the term jitter as marketing material for DACs is peppered with it. Typical specs might be “10 picoseconds of jitter” or a statement that some “femtoclock” is used for the DAC oscillator. Please ignore all such talk! For one thing, we don’t care how accurate a DAC clock is. I can slow down or speed up music by 0.1 percent and you would have no idea. That picosecond number is worthless because jitter comes in all forms and it is the nature of it which determines audibility, not what its single value sum total is.
Note also that often manufacturers give jitter specs for the clock that drives the DAC. This is of no interest to us as we don’t listen to that clock. We listen to the analog output of the DAC. That analog output may or may not be influenced by some variations of the DAC clock. Importantly, jitter and noise can be induced into the output of the DAC that do not originate from the oscillator directly.
Using FFT analysis we can tease out all the unwanted jitter, noise and spurious tones from the analog output of the DAC. We could use any sine wave we want but since jitter increases proportionally with frequency, we would want to use a higher frequency than 1 kHz we have focused on until now.
The late Julian Dunn (one our luminaries in digital audio) proposed a test signal called the J-test (jitter-test) that has become the industry standard. I am going to explain what it is but if you don’t understand it, it is fine. I will teach you what the graph shows regardless.
The J-test signal is a square wave that runs at one quarter of our digital audio sampling rate. I use 48 kHz for my jitter test so one quarter of that would be 12 kHz. Notice that I said this is a square wave, not sine wave. If we feed an ideal DAC a 12 kHz digital square wave, we actually get a pure sine wave at 12 kHz! How can this be? A square wave can be decomposed into an infinite number of sine waves that are odd harmonics of each other. So if the primary frequency of square wave is 12 kHz, if we decompose it with FFT, we get 12 kHz, 36 kHz, 60 kHz and so on. A DAC running at 48 kHz sampling truncates everything above half its sampling rate or 24 kHz. This means that the third harmonic (36 kHz) and higher all get truncated leaving us with one sine wave: 12 kHz.
So yes, if we band limit a square wave, we turn it into a pure sine wave. To demonstrate this in a real system, we can ask the APx555 to generate a 1 kHz square wave and show its spectrum using FFT. As you see in Figure 7 we have our primary/fundamental frequency of at 1 kHz, followed by a sequence of odd harmonics at 3, 5, 7 kHz, etc.
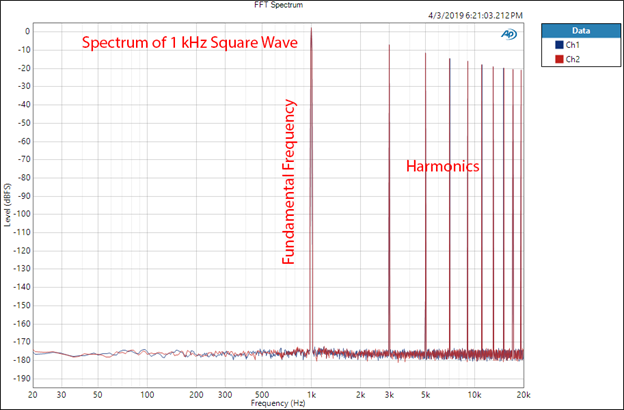
Figure 7: Spectrum of a 1 kHz Square Wave.
Why do we use a square wave if all we want is a sine wave? The reason is that by using a fixed digital value representing the top and bottom of a square wave, we have full control over the digital samples. We can use that knowledge by picking digital values that can be manipulated easily unlike fractional values representing a sine wave. To wit, a j-test signal embeds a second square wave inside the first one that causes all the PCM bits to flip every so many Hertz (250 Hz for 48 kHz).
For my testing, I use 24-bit j-test signal. This means that the 250 Hz square wave levels correspond to the rightmost bit of the 24-bit signal. Relative to full amplitude at 0 dBFS, the 250 Hz will be at -144 dB as shown in Figure 8.
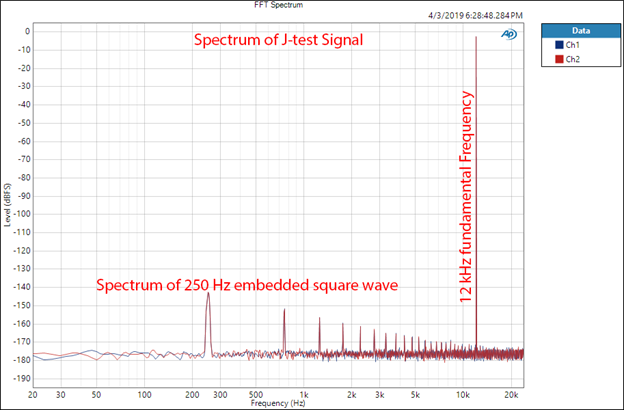
Figure 8: Spectrum of J-test jitter test signal.
Note that the vertical scale is dBFS which means we are analyzing digital samples here, not analog. This is why the noise floor is at a whopping -180 dBFS! A real DAC will struggle to do better than 20 bits so when measuring its analog output, we won’t be seeing any of the 250 Hz spikes.
Why put the 250 Hz square wave in there if we never see it in the output of the real DAC? When J-test was invented, it was designed to find jitter induced when long runs of AES or S/PDIF cables were used. The toggling would cause all the bits to shift from one value to another, exaggerating sources of jitter there.
Most of us use USB or HDMI for audio over short cables so the above cable sensitivity is not a concern for us. What is a concern for us is if toggling all those bits inside a DAC causes the analog output of the DAC to change to the same tune. In other words, it is possible for digital activity in a not-so-well-designed DAC to bleed into its sensitive analog stage. Figure 9 shows an example of such interference. We have our 12 kHz pure tone, as we should. But we also get a symmetrical set of spikes that are reduced in amplitude with odd multiples of 250 Hz, telling us it is the square wave in J-test causing it.
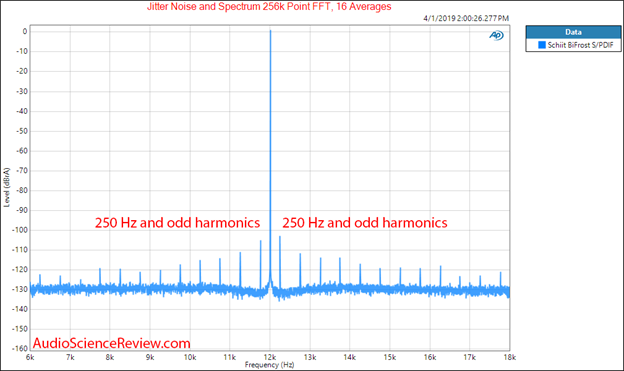
Figure 9: Spectrum of j-test signal from analog output of the DAC showing 250 Hz jitter.
If you couldn’t follow the previous explanation, that is fine. Whenever you see a j-test graph, focus on everything other than the main spike in the middle. These other tones, or noises are all unwanted.
Linearity
The job of every audio DAC is to convert a digital sample to corresponding analog value. This sounds easy but as levels get lower and lower, the DAC may have difficulty producing such analog voltages accuracy. The test for this is called linearity. A pure test tone is played and an analog voltage of the DAC captured. In order to exclude distortion and spurious responses, a very narrow filter excludes all but the test tone. To make the graph work, we sample a high output level (-20 dBFS in my testing) and compare everything to that (scaled of course). In an ideal case, we get a flat line as is the case for the Okto Research DAC8 in Figure 10.
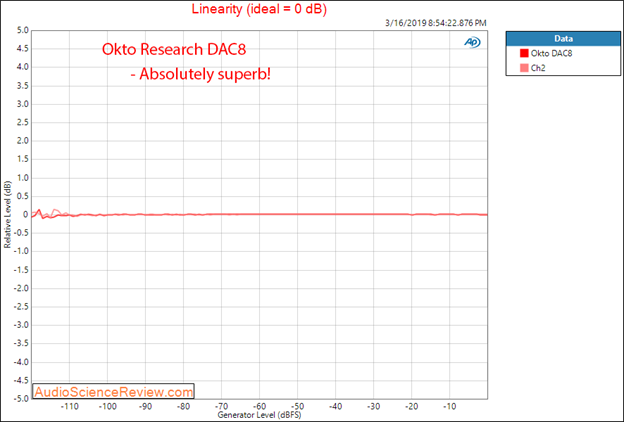
Figure 10: Linearity of DAC8 showing near perfect response down to 120 dBFS (20 bits).
Most DACs do well in Linearity test but there seems to have been a trend to go back to so called R2R DACs which tend to fail this test miserably if not exceptionally well implemented as we see in Figure 11:
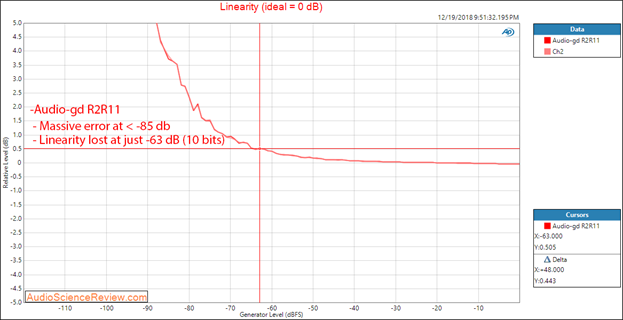
Figure 11: Example of a DAC showing very poor linearity, losing accuracy at just -63 dBFS or about 10 bits.
16-bit audio has a dynamic range of 96 dB so as a minimum we want to see a linearity that is ruler flat/0 dB up to at least that level.
Multitone Testing
An incorrect criticism against audio measurements is that we usually use a single tone and hence the result can’t possibly apply to music, which has countless tones. The argument misses the case that if a DAC distorts one tone, it will just as well distort one thousand. Anyway, to deal with the criticism, we can run more tones. In my case, I run 32 simultaneous tones at a sampling rate of 192 kHz. An ideal response would be just those 32 tones and nothing else. Nothing is perfect though so we get lots of extra spikes and raised noise floor when the DAC has a lot of distortion as seen in Figure 12.
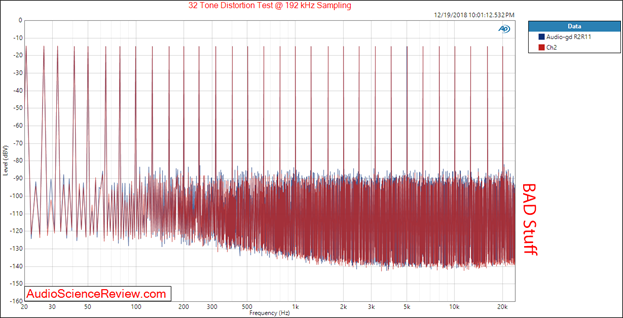
Figure 12: example of a DAC with high harmonic distortion.
We often call what is between the main tones “grass.” As such the less grass between the tones, the better. Figure 13 shows an example of a a very well performing DAC.
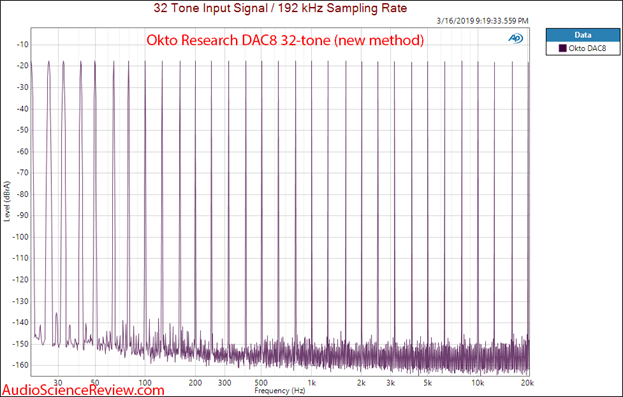
Figure 13: example of a DAC with very little harmonic/intermodulation distortion.
Intermodulation Distortion
Whenever we use more than one test tone, the resulting distortions shown are called intermodulation. The two tones interact with each other in a non-linear system and produce extra tones proportional to these tones. What is shown is not really different than harmonic distortion but has one key value: we can see all the distortions within the audible band. With harmonic distortion, we need to have wider bandwidth to capture the harmonics of anything above 11 kHz.
Over the years and decades, different sets of tones have been promoted to be used for measuring intermodulation. I use the SMPTE version, which is 60 Hz plus 7 kHz. The 60 Hz tone is useful because some devices have trouble reproducing lower frequencies (due to lack of a power supply current reservoir, for example). The 7 kHz is the opposite and tests the ability of the DAC to reproduce higher frequencies than 1 kHz we typically use for audio testing.
Figure 14 shows an example of a DAC (in red) that has very low intermodulation distortion. The graph is split into two domains: the declining and rising portion. The intermodulation test starts with our signal pairs at very low levels (-60 dBFS). As a result, noise dominates the measurement as indicated by the fact that when we increase the signal sources (less negative dBFS values), the measured “distortion” reduces. It is not the distortion that is reducing but the amount of noise captured in the intermodulation distortion detector. At some value, the level of noise becomes negligible and we hit the floor in intermodulation (noise +) distortion.
As we keep increasing the amplitude of our IMD tone pairs, some DACs start to produce increasingly more distortion and that shows up in the IMD curve reversing direction and going back up. In the case of the DAC in red, this occurs around -7 dBFS. Fortunately this is a very well behaved DAC and the rise is very slight until we get to the full value (0 dBFS).
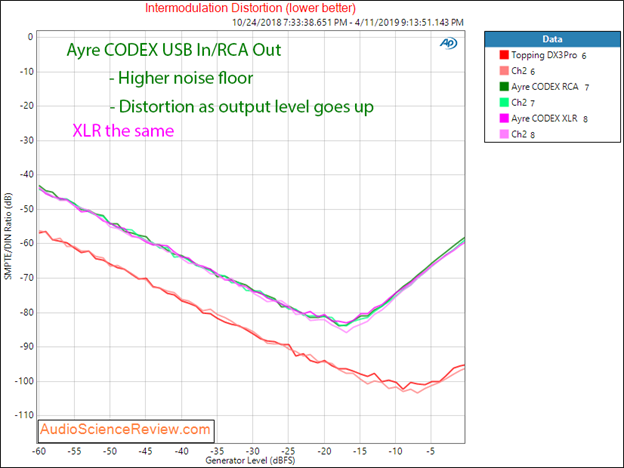
Figure 14: example of good intermodulation (red) and not so good (green/pink).
Contrast that with the DAC in green/pink where it not only has higher noise level (as seen by the higher position of the curve in its downward segment) but has distortion that sets in around -17 dBFS and keeps getting worse. This DAC uses an output amplifier (“buffer”) without feedback which usually translates into higher distortion levels.
After testing countless DACs an interesting pattern emerged with DAC products that use a DAC chip from ESS, which is one of the major silicon providers. Take a look at the intermodulation distortion of the DAC in green in Figure 15.
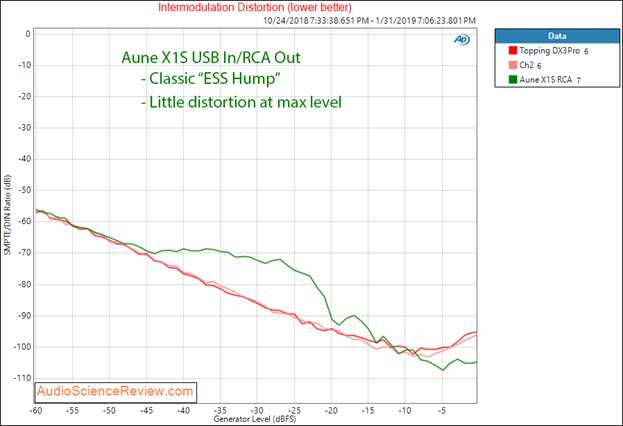
Figure 15: example of intermodulation distortion at mid-levels from ESS DACs.
Notice how the curve all of a sudden starts to rise around -45 dB but then returns back to normal around -10 dB. In other words, such DACs have unusually high intermodulation distortion when we have intermediate digital audio samples, not maximum as is usually the case. This occurs in so many ESS DAC chip-based designs that I have coined the term “ESS IMD hump.” The rising distortion shows up in vast majority of DACs using this series of ESS chips but interestingly a few notable designs manage to get it right such as Benchmark Design DAC3 and OPPO UDP-205.
Reconstruction Filter Response
Sampling theorem mandates a filter on the output of the DAC to get rid of “out of band” (high frequency) spurious response. DAC chip and system designers resort to different algorithms for this low-pass filter, as there are tradeoffs with respect to how fast the out of band data is filtered out and the flatness of the in-band spectrum. In addition, it is fashionable these days to design filters that have certain characteristics in the time domain (e.g. no ringing prior to an impulse).
To test for the filter response, we feed the DAC random white noise, which naturally has infinite bandwidth. The response of the low pass filter becomes obvious once we capture the output of the DAC and convert it to the frequency domain using FFT. Figure 16 shows an example of this as I change the filter settings in the DAC.
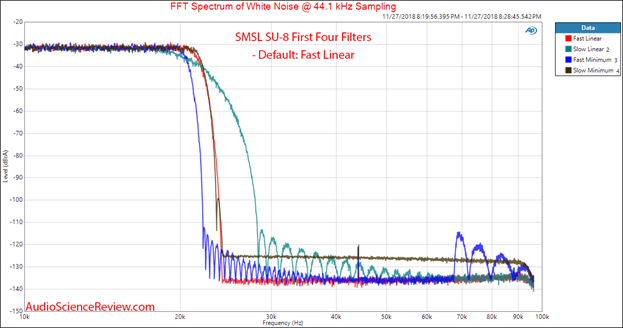
Figure 16: example of different DAC output filters.
The audibility impact of such filters is likely very low to non-existent so I don’t put a lot of value on this test.
Square Wave Testing
As I noted in the description of the low-pass filter in the DAC, there is interest in using filters that have certain time domain response. To detect this behavior, we use a square wave, which also has infinite bandwidth (odd harmonics to infinity). Classic filters used in DACs “ring” (oscillate) up and down before and after the sharp transitions in the square wave signal as seen in Figure 17. Note that a square wave (or impulse signal used as a substitute) does not exist in real life. Nothing in nature suddenly goes from 0 to a super high value in one sample. So be careful in buying into the marketing line of such and such time domain response is better.
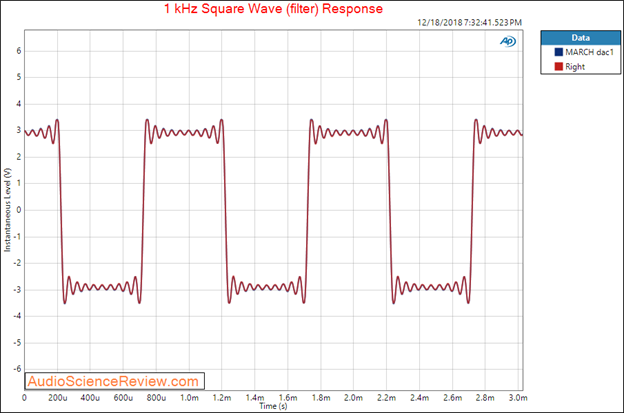
Figure 17: square wave response of a DAC showing classic ringing before and after the transition from low to high and vice versa.
Aside from the filter characteristic, square wave tones often show other problems such as clipping of the top of the signal. Figure 18 shows an example of this.
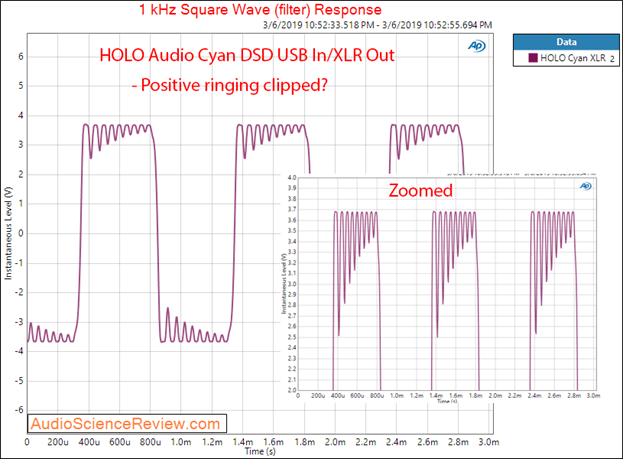
Figure 18: example of a DAC which clips the tops of the waveform.
This should not happen. The likely cause is internal math that doesn’t allow for an overflow above a maximum digital value.
Summary
I am hoping that by now you have a better understanding of how the performance of DACs (whether stand-alone or part of your AVR or A/V processor) can be characterized. As much as we like to assume DAC technology has matured, there are many subpar implementations. Price seems to be no predictor of performance. There are $99 DACs that outperform multi-thousand-dollar DACs by a wide margin. Seek out measurements of DACs so that you know how well engineered it is. Strive for performance that assures transparency with respect to audible noise and distortion.
Note: this article was published earlier this year in Widescreen Review Magazine.
Amir Majidimehr is the founder of audio/video/integration/automation company, Madrona Digital (madronadigital.com). Prior to that, he spent over 30 years in the computer and broadcast/consumer video industries at leading companies from Sony to Microsoft, always pushing to advance the state-of-the-art in delivery and consumption of digital media. Technologies developed in his teams are shipped in billions of devices from leading game consoles and phones to every PC in the world and are mandatory in such standards as Blu-ray Disc. He retired as Corporate Vice President at Microsoft in 2007 to pursue other interests, among which is a site dedicated to audio reviews and science called AudioScienceReview.com.
A detailed tutorial on how one can characterize the true performance of DACs (whether stand-alone or part of your AVR or A/V processor).
Without any formal training, most of us understand basic analog measurements such as frequency response. The concepts there are intuitive: any deviation from flat amplitude at any frequency shows an anomaly. Step into digital audio such as Digital To Analog Converters (DAC) the game becomes much more complex, spanning many domains of audio from signal processing to psychoacoustics. Do you know what dBFS is? How about composition of a square wave?
You might think digital audio is “perfect” and hence there is no need to measure such devices. That is not the case. While digital data is there forever, the moment you convert it to sound, it is an analog voltage that is ideally accurate to 24 bits. Turns out this is impossible in real life but many DACs fall way short of what can be done. Some DACs even fail to get to 16 bits let alone 24 bits.
Many DAC manufacturers use off-the-shelf DAC chips from the same few silicon providers. Alas, two DAC implementations using identical DAC chips can have very different performance. Sadly, price, brand reputation, designer behind the product, glowing reviews and market adoption do not predict performance. I have tested over 120 DACs so far [now over 220] and the results are all over the place. Some no name low ost DACs have exceptional performance. Others from very well-respected companies retailing for thousands of dollars fail miserably when measured the same way.
To give you a sense of how varied the performance of DACs are, take a look at Figure 1. This is an ordered ranking of “SINAD” ratings for 118 DACs. SINAD is the ratio of signal over noise summed with distortion. The higher the SINAD, the lower the amount of noise and distortion. The range of SINADs in the test DACs in Figure 1 is an incredible 55 dB to 118! Remember, dB is a logarithmic scale so even small differences can be significant.
Figure 1: SINAD (distortion & noise) rating of a range of products tested at AudioScienceReview.com
Since there are product variations and test conditions that vary somewhat, I don’t suggest readers look too closely at the SINAD numbers. Instead, go by what “bucket” they fall in based on color-coding. For best performance you want products in the blue bucket and avoid those in red.
We are getting ahead of ourselves though. Let’s dig into what such measurements mean and how to evaluate them.
Instrumentation
Audio measurements are performed using specialized instruments for this purpose. While you can perform some of these measurements using a good audio interface/sound card (ADC) and appropriate software, I have yet to find a combination that replicates the same as what can be done with dedicated audio measurement hardware. These devices run in a “closed loop.” meaning they can change one or two parameters, measure the output of the DAC, and then iterate. This gives us data across a range of operating points which can uncover issues that are not visible with “static” measurements.
The leader in audio instrumentation is Audio Precision. Their analyzers transformed the audio measurement industry back in 1990s and they have continued to maintain their lead until today. Using them means that there is a good chance someone else has access to them and can replicate the measurements. Unfortunately these analyzers are not cheap. The APx555 model that I use has a retail price of $28,000.
There are lower cost models (from other manufacturers such as Prism Sound) but you give up performance. In the context of measuring state-of-the-art DACs, we need to make sure the analyzer’s own distortion and noise are negligible compared to what is being measured. To give you an idea, the APx555 will score above 120 in the SINAD test in Figure 1. It gets there using fancy signal processing and use of two Analog to Digital Converts (ADCs) in parallel. The APx555 is essentially distortionless.
A number of (good) manufactures include measurements from Audio Precision although some are from the older “2700” series system. So learning how the Audio Precision measurements work in this article, will help you understand those specifications too. Of note, the vast majority of companies who provide such detailed graphs perform well and get high praise from me in my reviews. Lack of measurements graphs usually means the company either never measured the device or don’t feel like the measurements provide a positive image of the product. Both are bad news if you are a consumer.
The Dashboard
The APx555 has a real-time mode where the analyzer is constantly measuring the performance of a device. I have configured that so that in a single snapshot, we get a good idea of how well a DAC is performing. I have coined this the “dashboard” and you can see a sample of it in Figure 2. This is a high-performance multi-channel DAC from a small European company called “Okto Research.”
Figure 2: Dashboard view of Okto Research DAC8
This is a USB DAC and the APx555 Audio Precision analyzer is controlling it using that interface. You can tell this in the footnote in green with the term “ASIO.” ASIO is an audio driver interface that the APx555 uses to talk to the USB DAC (it unfortunately does not support any other interface as of this writing). If I were using S/PDIF or Optical interfaces to communicate with the DAC, those would show up instead.
Next to the output interface we see 44100 which is the sampling rate selected. 44100 is the sampling rate for CD and almost all streaming audio services. This can easily be changed and I do that for other tests (e.g. jitter). Since CD-based, 44.1 kHz sampling is so popular, it makes sense to focus on that in our dashboard.
The next text in green says the select input is Analog Balanced and that is exactly what it is. The Okto Research DAC8 only has XLR balanced outputs so that is what I am measuring. If I were testing RCA connections, it would say “unbalanced” there instead.
“200 Kohm” is the input impedance of the Audio Precision analyzer when testing XLR balanced connections. This is a very high impedance meaning the analyzer essentially puts no load on the output of the DAC and usually represents the best performance it can produce. If you have a pre-amp with very low input impedance, you may face issues not represented here although such devices tend to be very rare.
Next bit of text is not important (“5.000 Vrms”). That just says what the scale in the top left pane is. So ignore that.
The last text in the status line is very important as it shows the measurement bandwidth. Even though the APx555 analyzer is designed for audio, it can measure well outside of our hearing range to 1 Megahertz. I use such wide bandwidth when testing class D amplifiers as they create switching noise in hundreds of kilohertz. For DACs in the Dashboard view, I limit the bandwidth to 22.4 kHz, which is just above normal hearing range. And that is what you see in that text for the upper bound.
The lower band says “AC (< 10 Hz)” means that we are NOT measuring down to DC (0 Hz). A DC offset can upset the measurement system so unless there is a good reason for it (e.g. measuring frequency response), I use the “AC” measurement filter that ignores extremely low frequencies below 10 Hz.
The above are the test parameters. Everything else is analysis of what is coming out of the DAC. Let’s dig into those.
On top left we see a waveform. The digital generator in APx555 has been set to output a 1 kHz tone and that is what we see in that waveform display. The sample depth is 24 bits, so we have extreme accuracy here. The DAC takes these “perfect” digital samples and generates an analog waveform from it. That is what we are looking at in the top left. I call this the “time domain” display to contrast it from the FFT, which is the frequency domain of the same signal (explained later).
Figure 3: Audio Precision APx555 digital audio generator panel.
I have shown the digital frequency generator panel in APx555 in Figure 3. As you see, I can set the Frequency to whatever I want. 1 kHz is the industry norm for a lot of measurements so that is what I am using in this dashboard view.
The “level” or amplitude of the signal has a funny scale: dBFS. This stands for decibels (dB) from Full Scale. In digital domain, there is no concept of voltages. Everything is just a number. So we rely on a relative, logarithmic scale. 0 dBFS is full amplitude within the format we have set (24-bit PCM). Since this is a dB scale, every reduction of the dBFS by 6 dB represents halving the analog output voltage of the DAC.
You often read in my reviews that so and so dB value is so many bits. We can convert dB to equivalent number of bits (ENOB) by simply dividing the dB value by 6 (this is a bit of approximation). So if I set the digital generator to -120 dBFS (remember 0 dBFS is maximum so all allowable numbers are negative or less than max), it means I am telling the DAC to reproduce a voltage that is represented by 120/6 = 20 bits. If I set it to -96 dBFS then I am asking the DAC to output a level closest to what 16-bit audio samples would represent (16 * 6 = 96 dB).
For the dashboard as shown, the test is usually at 0 dBFS. I say usually because when measuring RCA/unbalanced output we like to see a nominal voltage output from DAC of around 2 volts. Anything less would mean that the DAC may not have enough output to drive your amplifier to max power levels depending on its sensitivity. For the balanced XLR output, this doubles to 4 volts. In our sample dashboard we see 3.1316 volts (RMS), which is too low. The company in question has taken this feedback and plans to release products at 4 volts.
If the DAC output voltage is higher than these nominal values, I often reduce the dBFS incrementally to get it down to where they should be. This sometimes reduces the distortion levels and improves SINAD. Sometimes it doesn’t make a difference.
The next “meter” is on the bottom left and represents the measured frequency from the output of the DAC. Recall that we told our DAC to produce a 1 kHz tone. What we see coming from the DAC is a bit off at 0.99998 kHz. The reason for this is that all DACs have a local clock that has some accuracy error. In this case, it is running a hair slow. This is why if you put two DACs playing side by side, they can drift away from each other over time. This field is informative and usually doesn’t show an issue.
Now let’s focus on the all-important “FFT” window on top right. That is a mathematical conversion of the waveform to the left (the sine wave) into its fundamental components in frequency domain. We think that we told the DAC to produce a 1 kHz tone and that is exactly what it has done. That assumes a perfect DAC that is perfectly linear meaning it produces outputs with infinite accuracy to what is being input. All DACs have conversion errors which create non-linearity. This means that a single sine wave going in, will result in that sine wave coming out plus harmonic distortion (multiples of the source frequency). In addition to harmonic distortion, we also have noise and often spurious tones mixed in that are unrelated to what we asked the DAC to do.
Because the non-linearities in audio are quite small relative to the main signal (a 1 kHz tone in this case), we cannot see them in the sine wave in top right (time domain signal). Conversion to frequency domain nicely takes apart the output of the DAC into subcomponents showing every distortion and spurious tone with ease.
The dashboard view shows that the DAC being measured has a second harmonic (2 kHz) at below -130 dB (1 kHz signal has been set to 0 dB). Translating this into bit depth, the second harmonic distortion is below 21 bits of resolution. This is well below an audible level as our best-case hearing has dynamic range of 116 dB. In that regard, even the taller third harmonic at -128 dB or so is by far below audibility levels. In other words, this DAC is objectively and provably transparent to our hearing when it comes to distortion.
When creating FFT displays, we tell the system how many audio samples to use. In the case of the dashboard, this is set to 32000, which gives very good resolution to see distortion spikes. We can increase this number to over 1 million in APx555. I use 256,000 when showing a dedicated 1 kHz FFT spectrum as seen in Figure 4. The DAC in this test has much so we see a “spray” (series) of distortion spikes, which are worse in the blue channel.
For this measurement, I have set the maximum frequency much higher allowing us to see what is above our hearing range of 20 kHz. We see a few “spurs” (spurious tones) between 45 kHz and 50 kHz. While not audible, good engineering means that the DAC would not spit out such unwanted frequencies.
Figure 4: FFT spectrum of distortion and noise in a DAC.
Let’s go back to our dashboard and look at the THD+N Ratio meter. This is a single figure of merit for audio gear that has been around forever. The measurement was performed by playing a 1 kHz tone, capturing that output, and filtering out the 1 kHz with a very narrow notch filter. Anything that remains is either distortion or noise. Sum them all and you get THD+N. With our modern instrumentation we can choose any frequency for testing but since the tradition is 1 kHz, I have stayed with that in the dashboard.
Important note: you may be tempted to read the DAC noise level from the noisy part of the graph/floor in the FFT. DO NOT DO THIS! The true noise floor of a DAC is much higher. When we perform FFT, the more points we use, the lower the noise floor becomes. This is called “FFT gain” and is a good thing as it allows us to see distortion products that may be well buried inside the noise floor of the DAC (and ADC in the measurement gear). The gain can be as much as 30 dB to 40 dB lower than reality! Math can be used to back out this gain using the number of points.
Instead of doing that, we can measure the sum of distortions+noise in the form of THD+N (Total Harmonic Distortion + Noise). This is what is shown in our THD+N Ratio meter below the FFT. THD+N is a very common figure of merit quoted in many product specs.
Below THD+N is the SINAD figure I referenced earlier. SINAD is actually the same value as THD+N but expressed in dB relative to the signal amplitude. This is good because we can, at a glance, compare the SINAD to our hearing dynamic range of 116 dB and know if we are better or worse than it. This is a back of an envelope computation for audibility so don’t completely run with it. Use it as a first order approximation. If a DAC has better SINAD than 116 dB, then we have very high confidence of transparency. If the SINAD is below 116 dB, then the nature of the distortion spectrum will tell us if the distortion is audible or not (i.e. we have to look at the FFT).
THD+N Versus Frequency
Our dashboard view is a performance snapshot at 1 kHz. Performance of devices in general varies as source frequency changes. It is very easy to create such a “sweep” in APx555, having it vary the digital generator source frequency and measuring the THD+N at that point from the output of the DAC. You can see this in Figure 5.
Figure 5: THD+N (distortion+noise) versus Source Frequency.
Note that the measurement in Figure 5 has a bandwidth of 90 kHz unlike the dashboard, which uses 22.4 kHz. Why so much higher? Harmonics are multiples of a frequency. In the dashboard, we use a 1 kHz tone so its multiples all the way to 22 kHz can be captured in 22.4 kHz of bandwidth. Here we are going up to 20 kHz in source frequency so if we stop at just 22.4 kHz, just as well, we won’t capture any harmonic distortion as the second harmonic is at 40 kHz. By using 90 kHz bandwidth we are able to capture up to a fourth harmonic of 20 kHz, which measures most of the distortion we are going to see.
Alas, the higher bandwidth of 90 kHz means that we not only capture harmonic distortion but also any ultrasonic noise and spurious tones. We can see this once again in Figure 6 if we measure the Schiit BiFrost DAC.
Figure 6: THD+N versus frequency for a lower performing DAC.
The rise in THD+N in one channel is most likely due to unwanted ultrasonic tones than actual harmonic distortion. Notice how much worse that graph in blue is compared to the DAC in red which is a low-cost ($99) bare board DAC (“Khadas Tone Board”).
The most important lesson is that every THD+N graph or specification must include the bandwidth used for measurement. Otherwise the data cannot be interpreted.
Note that some manufactures and reviewers use “a-weighting” when stating THD+N. This is a standardized filter that equalizes the output of the DAC to have less amplitude at low and high frequencies. This is said to better match our hearing. Alas the graph is a too simplistic view of our hearing so I don’t use it. In almost all cases, a-weighting reduces the THD+N so it is popular with manufacturers.
Jitter and Noise
Most audiophiles have heard of the term jitter as marketing material for DACs is peppered with it. Typical specs might be “10 picoseconds of jitter” or a statement that some “femtoclock” is used for the DAC oscillator. Please ignore all such talk! For one thing, we don’t care how accurate a DAC clock is. I can slow down or speed up music by 0.1 percent and you would have no idea. That picosecond number is worthless because jitter comes in all forms and it is the nature of it which determines audibility, not what its single value sum total is.
Note also that often manufacturers give jitter specs for the clock that drives the DAC. This is of no interest to us as we don’t listen to that clock. We listen to the analog output of the DAC. That analog output may or may not be influenced by some variations of the DAC clock. Importantly, jitter and noise can be induced into the output of the DAC that do not originate from the oscillator directly.
Using FFT analysis we can tease out all the unwanted jitter, noise and spurious tones from the analog output of the DAC. We could use any sine wave we want but since jitter increases proportionally with frequency, we would want to use a higher frequency than 1 kHz we have focused on until now.
The late Julian Dunn (one our luminaries in digital audio) proposed a test signal called the J-test (jitter-test) that has become the industry standard. I am going to explain what it is but if you don’t understand it, it is fine. I will teach you what the graph shows regardless.
The J-test signal is a square wave that runs at one quarter of our digital audio sampling rate. I use 48 kHz for my jitter test so one quarter of that would be 12 kHz. Notice that I said this is a square wave, not sine wave. If we feed an ideal DAC a 12 kHz digital square wave, we actually get a pure sine wave at 12 kHz! How can this be? A square wave can be decomposed into an infinite number of sine waves that are odd harmonics of each other. So if the primary frequency of square wave is 12 kHz, if we decompose it with FFT, we get 12 kHz, 36 kHz, 60 kHz and so on. A DAC running at 48 kHz sampling truncates everything above half its sampling rate or 24 kHz. This means that the third harmonic (36 kHz) and higher all get truncated leaving us with one sine wave: 12 kHz.
So yes, if we band limit a square wave, we turn it into a pure sine wave. To demonstrate this in a real system, we can ask the APx555 to generate a 1 kHz square wave and show its spectrum using FFT. As you see in Figure 7 we have our primary/fundamental frequency of at 1 kHz, followed by a sequence of odd harmonics at 3, 5, 7 kHz, etc.
Figure 7: Spectrum of a 1 kHz Square Wave.
Why do we use a square wave if all we want is a sine wave? The reason is that by using a fixed digital value representing the top and bottom of a square wave, we have full control over the digital samples. We can use that knowledge by picking digital values that can be manipulated easily unlike fractional values representing a sine wave. To wit, a j-test signal embeds a second square wave inside the first one that causes all the PCM bits to flip every so many Hertz (250 Hz for 48 kHz).
For my testing, I use 24-bit j-test signal. This means that the 250 Hz square wave levels correspond to the rightmost bit of the 24-bit signal. Relative to full amplitude at 0 dBFS, the 250 Hz will be at -144 dB as shown in Figure 8.
Figure 8: Spectrum of J-test jitter test signal.
Note that the vertical scale is dBFS which means we are analyzing digital samples here, not analog. This is why the noise floor is at a whopping -180 dBFS! A real DAC will struggle to do better than 20 bits so when measuring its analog output, we won’t be seeing any of the 250 Hz spikes.
Why put the 250 Hz square wave in there if we never see it in the output of the real DAC? When J-test was invented, it was designed to find jitter induced when long runs of AES or S/PDIF cables were used. The toggling would cause all the bits to shift from one value to another, exaggerating sources of jitter there.
Most of us use USB or HDMI for audio over short cables so the above cable sensitivity is not a concern for us. What is a concern for us is if toggling all those bits inside a DAC causes the analog output of the DAC to change to the same tune. In other words, it is possible for digital activity in a not-so-well-designed DAC to bleed into its sensitive analog stage. Figure 9 shows an example of such interference. We have our 12 kHz pure tone, as we should. But we also get a symmetrical set of spikes that are reduced in amplitude with odd multiples of 250 Hz, telling us it is the square wave in J-test causing it.
Figure 9: Spectrum of j-test signal from analog output of the DAC showing 250 Hz jitter.
If you couldn’t follow the previous explanation, that is fine. Whenever you see a j-test graph, focus on everything other than the main spike in the middle. These other tones, or noises are all unwanted.
Linearity
The job of every audio DAC is to convert a digital sample to corresponding analog value. This sounds easy but as levels get lower and lower, the DAC may have difficulty producing such analog voltages accuracy. The test for this is called linearity. A pure test tone is played and an analog voltage of the DAC captured. In order to exclude distortion and spurious responses, a very narrow filter excludes all but the test tone. To make the graph work, we sample a high output level (-20 dBFS in my testing) and compare everything to that (scaled of course). In an ideal case, we get a flat line as is the case for the Okto Research DAC8 in Figure 10.
Figure 10: Linearity of DAC8 showing near perfect response down to 120 dBFS (20 bits).
Most DACs do well in Linearity test but there seems to have been a trend to go back to so called R2R DACs which tend to fail this test miserably if not exceptionally well implemented as we see in Figure 11:
Figure 11: Example of a DAC showing very poor linearity, losing accuracy at just -63 dBFS or about 10 bits.
16-bit audio has a dynamic range of 96 dB so as a minimum we want to see a linearity that is ruler flat/0 dB up to at least that level.
Multitone Testing
An incorrect criticism against audio measurements is that we usually use a single tone and hence the result can’t possibly apply to music, which has countless tones. The argument misses the case that if a DAC distorts one tone, it will just as well distort one thousand. Anyway, to deal with the criticism, we can run more tones. In my case, I run 32 simultaneous tones at a sampling rate of 192 kHz. An ideal response would be just those 32 tones and nothing else. Nothing is perfect though so we get lots of extra spikes and raised noise floor when the DAC has a lot of distortion as seen in Figure 12.
Figure 12: example of a DAC with high harmonic distortion.
We often call what is between the main tones “grass.” As such the less grass between the tones, the better. Figure 13 shows an example of a a very well performing DAC.
Figure 13: example of a DAC with very little harmonic/intermodulation distortion.
Intermodulation Distortion
Whenever we use more than one test tone, the resulting distortions shown are called intermodulation. The two tones interact with each other in a non-linear system and produce extra tones proportional to these tones. What is shown is not really different than harmonic distortion but has one key value: we can see all the distortions within the audible band. With harmonic distortion, we need to have wider bandwidth to capture the harmonics of anything above 11 kHz.
Over the years and decades, different sets of tones have been promoted to be used for measuring intermodulation. I use the SMPTE version, which is 60 Hz plus 7 kHz. The 60 Hz tone is useful because some devices have trouble reproducing lower frequencies (due to lack of a power supply current reservoir, for example). The 7 kHz is the opposite and tests the ability of the DAC to reproduce higher frequencies than 1 kHz we typically use for audio testing.
Figure 14 shows an example of a DAC (in red) that has very low intermodulation distortion. The graph is split into two domains: the declining and rising portion. The intermodulation test starts with our signal pairs at very low levels (-60 dBFS). As a result, noise dominates the measurement as indicated by the fact that when we increase the signal sources (less negative dBFS values), the measured “distortion” reduces. It is not the distortion that is reducing but the amount of noise captured in the intermodulation distortion detector. At some value, the level of noise becomes negligible and we hit the floor in intermodulation (noise +) distortion.
As we keep increasing the amplitude of our IMD tone pairs, some DACs start to produce increasingly more distortion and that shows up in the IMD curve reversing direction and going back up. In the case of the DAC in red, this occurs around -7 dBFS. Fortunately this is a very well behaved DAC and the rise is very slight until we get to the full value (0 dBFS).
Figure 14: example of good intermodulation (red) and not so good (green/pink).
Contrast that with the DAC in green/pink where it not only has higher noise level (as seen by the higher position of the curve in its downward segment) but has distortion that sets in around -17 dBFS and keeps getting worse. This DAC uses an output amplifier (“buffer”) without feedback which usually translates into higher distortion levels.
After testing countless DACs an interesting pattern emerged with DAC products that use a DAC chip from ESS, which is one of the major silicon providers. Take a look at the intermodulation distortion of the DAC in green in Figure 15.
Figure 15: example of intermodulation distortion at mid-levels from ESS DACs.
Notice how the curve all of a sudden starts to rise around -45 dB but then returns back to normal around -10 dB. In other words, such DACs have unusually high intermodulation distortion when we have intermediate digital audio samples, not maximum as is usually the case. This occurs in so many ESS DAC chip-based designs that I have coined the term “ESS IMD hump.” The rising distortion shows up in vast majority of DACs using this series of ESS chips but interestingly a few notable designs manage to get it right such as Benchmark Design DAC3 and OPPO UDP-205.
Reconstruction Filter Response
Sampling theorem mandates a filter on the output of the DAC to get rid of “out of band” (high frequency) spurious response. DAC chip and system designers resort to different algorithms for this low-pass filter, as there are tradeoffs with respect to how fast the out of band data is filtered out and the flatness of the in-band spectrum. In addition, it is fashionable these days to design filters that have certain characteristics in the time domain (e.g. no ringing prior to an impulse).
To test for the filter response, we feed the DAC random white noise, which naturally has infinite bandwidth. The response of the low pass filter becomes obvious once we capture the output of the DAC and convert it to the frequency domain using FFT. Figure 16 shows an example of this as I change the filter settings in the DAC.
Figure 16: example of different DAC output filters.
The audibility impact of such filters is likely very low to non-existent so I don’t put a lot of value on this test.
Square Wave Testing
As I noted in the description of the low-pass filter in the DAC, there is interest in using filters that have certain time domain response. To detect this behavior, we use a square wave, which also has infinite bandwidth (odd harmonics to infinity). Classic filters used in DACs “ring” (oscillate) up and down before and after the sharp transitions in the square wave signal as seen in Figure 17. Note that a square wave (or impulse signal used as a substitute) does not exist in real life. Nothing in nature suddenly goes from 0 to a super high value in one sample. So be careful in buying into the marketing line of such and such time domain response is better.
Figure 17: square wave response of a DAC showing classic ringing before and after the transition from low to high and vice versa.
Aside from the filter characteristic, square wave tones often show other problems such as clipping of the top of the signal. Figure 18 shows an example of this.
Figure 18: example of a DAC which clips the tops of the waveform.
This should not happen. The likely cause is internal math that doesn’t allow for an overflow above a maximum digital value.
Summary
I am hoping that by now you have a better understanding of how the performance of DACs (whether stand-alone or part of your AVR or A/V processor) can be characterized. As much as we like to assume DAC technology has matured, there are many subpar implementations. Price seems to be no predictor of performance. There are $99 DACs that outperform multi-thousand-dollar DACs by a wide margin. Seek out measurements of DACs so that you know how well engineered it is. Strive for performance that assures transparency with respect to audible noise and distortion.
Note: this article was published earlier this year in Widescreen Review Magazine.
Amir Majidimehr is the founder of audio/video/integration/automation company, Madrona Digital (madronadigital.com). Prior to that, he spent over 30 years in the computer and broadcast/consumer video industries at leading companies from Sony to Microsoft, always pushing to advance the state-of-the-art in delivery and consumption of digital media. Technologies developed in his teams are shipped in billions of devices from leading game consoles and phones to every PC in the world and are mandatory in such standards as Blu-ray Disc. He retired as Corporate Vice President at Microsoft in 2007 to pursue other interests, among which is a site dedicated to audio reviews and science called AudioScienceReview.com.
Attachments
Last edited: