Where does quantization noise come from.

[dasdoing]

on a sidenote https://www.audiocheck.net/blindtests_16vs8bit.php

 

[dasdoing]

and this

Dynamic Range, Dithering and Noise Shaping

Dithering, explained and demonstrated.

www.audiocheck.net

 

[torgeirs]

Going back in the patents history we can se the original PCM patent

US2272070A - Electric signaling system - Google Patents

The inventor only use the term noise. So to him, noise was noise

 

[Chromatischism]

All the engineering societies and references I know use "noise" for quantization noise.

Interesting. And I have only seen it referred to as an error, not noise, in the photo community (digitizing photons as they hit image sensors). Even in audio I'm seeing a lot of references to quantization error, which makes sense because it's not introduced from outside.

 

[DonH56]

Interesting. And I have only seen it referred to as an error, not noise, in the photo community (digitizing photons as they hit image sensors). Even in audio I'm seeing a lot of references to quantization error, which makes sense because it's not introduced from outside.

I am only vaguely familiar with it in the photo world so maybe they use different definitions? I am sure they use different standards for reference.

Quantization error leads to quantization noise, but also distortion; those IEEE Standards list a bunch of error sources. Not as bad as jitter; the last jitter testing I did for high-speed systems referenced something like 27 different types of jitter in the spec. Blah.

 

[wwenze]

Hearing people talk about lossy compression reminded me that video encode quality is often measured in PSNR (Peak Signal to Noise Ratio) Since the lower the bitrate the bigger the blocks.

At this point the result is clearly based on mathematical functions and highly reproducible (no ADC or time or analogue shzz), but it's still called noise.

 

[Tell]

Interesting. And I have only seen it referred to as an error, not noise, in the photo community (digitizing photons as they hit image sensors). Even in audio I'm seeing a lot of references to quantization error, which makes sense because it's not introduced from outside.

In audio it sounds like noise and is therefor called noise, in photography it doesn't look like noise though but instead looks more like bands if you look in gradients like a sky for example, so it's called banding instead, or posterization will do as well.
But yeah in both audio and image it is an error, just that it can be called other things as well depending how we experience it

 

[sq225917]

Its functionally Correlated error, and when compared to the original signal it's noise. Poor semantics.

 

[danadam]

Let's stick with not using the term "noise" because it leads to confusion.

https://www.ni.com/docs/en-US/bundle/daqhelp/page/quanterror.html

I also like the term "error". And then "distortion" if the error is correlated to the signal and "noise" if the error is not correlated to the signal.

Then you can say: "Quantization produces an error. This error could be a distortion. You can use dither to turn distortion into noise." and everything is clear and unambiguous.

But I guess that ship has sailed and "noise" seems to be the most popular replacement, sometimes with added correlated/uncorrelated.

 

[antcollinet]

I also like the term "error". And then "distortion" if the error is correlated to the signal and "noise" if the error is not correlated to the signal.

Then you can say: "Quantization produces an error. This error could be a distortion. You can use dither to turn distortion into noise." and everything is clear and unambiguous.

But I guess that ship has sailed and "noise" seems to be the most popular replacement, sometimes with added correlated/uncorrelated.

For me at the end of the day, potayto potahto.

16 bits and it is (except in extreme/unrealistic circumstances) inaudible. 24 bit and it is so far beyond inaudible it might as well not exist.

 

[DonH56]

I also like the term "error". And then "distortion" if the error is correlated to the signal and "noise" if the error is not correlated to the signal.

Then you can say: "Quantization produces an error. This error could be a distortion. You can use dither to turn distortion into noise." and everything is clear and unambiguous.

But I guess that ship has sailed and "noise" seems to be the most popular replacement, sometimes with added correlated/uncorrelated.

The references I cited (IEEE Standards) distinguish quantization noise from other error sources that cause distortion (e.g. harmonic, intermodulation, INL/DNL, and so forth). If you perfectly quantize the signal there will still be quantization noise, but no other errors (distortion).

Dither (noise decorrelation) is another (large) topic and, while it can spread correlated distortion spurs, does not in general "turn distortion into noise", at least per my standards.

In any event I'm out, I'll stick with defined industry standards rather than argue and make up my own.

 

[danadam]

I appreciate the red line is the difference between the original and the quantized signal

You can rearrange that equation as: the quantized signal (yellow) is the sum of the original (green) and the error (red). So what the DAC outputs (yellow) is a mix of the original and the error.

I just don't understand why quantizing is creating "noise" when in my head it's just modifying the original signal.

If not "noise", then what do (or did) you think this "just modifying" should do to the signal?

Which I guess then begs the question, how do we know if the signal contains noise or is in fact what it was supposed to sound like in the first place?!

If all we are left with is the quantized signal then we can't. If we have the original lying around then we can subtract one from the other and see what's left.

---

I don't know if it helps but I tried answering similar question here:

Quantization Noise 101: Where does SNR about 6N dB come from?

This post attempts to explain where the SNR = 6N dB approximation comes from. ASR does not have the symbol font available, and after an hour or so of trying to fix things, I ended up just pasting the whole thing as an image. Sorry about that! I did attach a PDF of the original.

www.audiosciencereview.com

Quantization Noise 101: Where does SNR about 6N dB come from?

Thanks for the pdf file. The equations are a bit too low res on the forum post. We really need a build in LaTeX editor on the forum :) There is a MathJax plugin for XenForo. Seems to be unmaintained, but may still be worth a try.

www.audiosciencereview.com

 

[tmtomh]

You can rearrange that equation as: the quantized signal (yellow) is the sum of the original (green) and the error (red). So what the DAC outputs (yellow) is a mix of the original and the error.


If not "noise", then what do (or did) you think this "just modifying" should do to the signal?


If all we are left with is the quantized signal then we can't. If we have the original lying around then we can subtract one from the other and see what's left.

---

I don't know if it helps but I tried answering similar question here:

Quantization Noise 101: Where does SNR about 6N dB come from?

This post attempts to explain where the SNR = 6N dB approximation comes from. ASR does not have the symbol font available, and after an hour or so of trying to fix things, I ended up just pasting the whole thing as an image. Sorry about that! I did attach a PDF of the original.

www.audiosciencereview.com

Quantization Noise 101: Where does SNR about 6N dB come from?

Thanks for the pdf file. The equations are a bit too low res on the forum post. We really need a build in LaTeX editor on the forum :) There is a MathJax plugin for XenForo. Seems to be unmaintained, but may still be worth a try.

www.audiosciencereview.com

Thanks (as always!) for the clear explanation. I'm thinking the one final piece of information that might make @teapea feel like this all fully makes sense would be a very mundane and practical piece of information: How does one capture the data necessary to plot a signal such that it can be shown at the moment when it's sampled but not yet quantized, as you have shown in the links you posted above (here's a screenshot)?

 

[danadam]

How does one capture the data necessary to plot a signal such that it can be shown at the moment when it's sampled but not yet quantized, as you have shown in the links you posted above (here's a screenshot)?

Well, I should have put "not yet quantized" in quotes. It was a digital file, so of course it was quantized. But I used high enough bit-depth to pretend (or simulate) that it was not quantized.

Here's how the files can be generated (files in attachment). For our pretend-not-quantized signal I'll use 16-bit (-b16). To have a bit more interesting waveform I'll generate 1 kHz sine with modulated amplitude:

sox -r44.1k -n -b16 A_not_quantized.wav synth 3 sin 1k synth sin amod 20 20 norm -4

Convert (without dither) to 8-bit (-b8) and reduce volume x0.03125 (that's 1/32 and 32 = 2^5). This will reduce bit-depth to 3 bits (8-5=3). Then increase the volume back x32.

sox -D A_not_quantized.wav -b8 tmp.wav vol .03125
sox -D tmp.wav -b16 B1_quantized_no_dither.wav vol 32

Subtract one from the other to isolate the quantization error:

sox -D -m -v1 B1_quantized_no_dither.wav -v -1 A_not_quantized.wav B2_error_no_dither.wav

The files look like this:


The same with dither (remove -D when reducing volume):

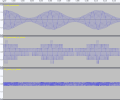
sox A_not_quantized.wav -b8 tmp.wav vol .03125
sox -D tmp.wav -b16 C1_quantized_with_dither.wav vol 32
sox -D -m -v1 C1_quantized_with_dither.wav -v -1 A_not_quantized.wav C2_error_with_dither.wav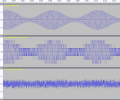

And just to confirm that B1 and C1 use only 3 bits:

]$ sox B1_quantized_no_dither.wav -n stats
...
Bit-depth       3/3

]$ sox C1_quantized_with_dither.wav -n stats
...
Bit-depth       3/3

 

[tmtomh]

Well, I should have put "not yet quantized" in quotes. It was a digital file, so of course it was quantized. But I used high enough bit-depth to pretend (or simulate) that it was not quantized.

Here's how the files can be generated (files in attachment). For our pretend-not-quantized signal I'll use 16-bit (-b16). To have a bit more interesting waveform I'll generate 1 kHz sine with modulated amplitude:

sox -r44.1k -n -b16 A_not_quantized.wav synth 3 sin 1k synth sin amod 20 20 norm -4

Convert (without dither) to 8-bit (-b8) and reduce volume x0.03125 (that's 1/32 and 32 = 2^5). This will reduce bit-depth to 3 bits (8-5=3). Then increase the volume back x32.

sox -D A_not_quantized.wav -b8 tmp.wav vol .03125
sox -D tmp.wav -b16 B1_quantized_no_dither.wav vol 32

Subtract one from the other to isolate the quantization error:

sox -D -m -v1 B1_quantized_no_dither.wav -v -1 A_not_quantized.wav B2_error_no_dither.wav

The files look like this:
View attachment 365522View attachment 365523

The same with dither (remove -D when reducing volume):

sox A_not_quantized.wav -b8 tmp.wav vol .03125
sox -D tmp.wav -b16 C1_quantized_with_dither.wav vol 32
sox -D -m -v1 C1_quantized_with_dither.wav -v -1 A_not_quantized.wav C2_error_with_dither.wav

View attachment 365524View attachment 365525

And just to confirm that B1 and C1 use only 3 bits:

]$ sox B1_quantized_no_dither.wav -n stats
...
Bit-depth       3/3

]$ sox C1_quantized_with_dither.wav -n stats
...
Bit-depth       3/3

That’s very clever and really cool - thanks!

 

[danadam]

Dither (noise decorrelation) is another (large) topic and, while it can spread correlated distortion spurs, does not in general "turn distortion into noise", at least per my standards.

I won't argue that I interpreted it correctly, but I took that phrase from: JAES vol 52 no 3 / "Pulse-Code Modulation - An Overview" - Lipshitz, Vanderkooy

Jaes V52 3 All PDF - PDFCOFFEE.COM

The Audio Engineering Society recognizes with gratitude the financial support given by its sustaining members, which ena...

pdfcoffee.com

p.208,209
The correlated distortion lines of Fig. 5(d) have been
turned into an innocuous white-noise floor by the TPDF-
dithered quantization.

p.209,210
It should thus be clear, and it is important to
realize, that the distortion has actually been converted into
a benign noise. It is not a question of noise masking or
“covering up” the distortion.

 

[DonH56]

I won't argue that I interpreted it correctly, but I took that phrase from: JAES vol 52 no 3 / "Pulse-Code Modulation - An Overview" - Lipshitz, Vanderkooy

Jaes V52 3 All PDF - PDFCOFFEE.COM

The Audio Engineering Society recognizes with gratitude the financial support given by its sustaining members, which ena...

pdfcoffee.com

View attachment 365530

IMO this is not the place to debate how Lipshitz and Vanderkooy differ in their definitions from the IEEE. They treat the quantization error as highly-correlated to the signal, which is true to the extent that the signal and sampling frequency are correlated, but in general the signal frequency and sampling frequency are independent and thus the quantization error "looks like" noise. The spurs are also related to the sample (FFT) size, of course. You can choose frequencies that are highly correlated and put all the error/noise into just a few FFT bins (theoretically one or two, I forget the limiting case), but I (and the IEEE) consider that a degenerate (not general) case. When sampling and signal frequencies are not locked, the samples "walk through" the signal, and the error signal looks (more) random. Locking frequencies, and choosing relatively prime relations that fit perfectly into the FFT size, are incredibly useful for testing and generate exactly the plots shown in that paper. I am certainly not going to say they are wrong, but our base definitions differ.

In any event I feel this discussion has wandered far beyond what the OP and most ASR readers will follow, nor do I think either of us is likely to change our fundamental definitions acquired over decades of use. I have a very vague memory of Temes or Candy (forget which one) stating they chose to define quantization "noise" partly to distinguish it from typical ("conventional") sources of distortion -- but I could be misremembering an ancient conversation (ca. 1980's). I should also note that, except for my own interest, I have not kept up with the AES since shortly after college (1980's) as my career took me into higher frequencies and the IEEE arena (for several years my boss led the IEEE committee that wrote the standards). I do know other organizations, let alone industry, do not always follow the IEEE.

 

[teapea]

If not "noise", then what do (or did) you think this "just modifying" should do to the signal?

This is a good question - I think I intuitively thought it would somehow change the tonality slightly.

 

[theREALdotnet]

16 bits and it is (except in extreme/unrealistic circumstances) inaudible. 24 bit and it is so far beyond inaudible it might as well not exist.

We should add: for practical intents and purposes. The above is being stated so often, it’s becoming a mantra. I think it’s worthwhile remembering under which circumstances it is true – when listening to music recorded within -40 to 0dbFS, in a listening chair 2-3m from the speakers.

Because if you’re looking for it, the loss of resolution is clearly audible, as are the differences between DACs. Play, for example, a mellow sine tone (200 or 400Hz) at -100dB, using the REW generator. This can only be done in 24bit, obviously. Put your ear next to the mid-woofer and be surprised by how differently DACs handle this task. Or, by how drastically adding dither (also in REW) will improve the result in virtually all cases.

So yes, quantisation can be heard, just not when playing a normal music recording.

 

[Tell]

So yes, quantisation can be heard, just not when playing a normal music recording.

Quantisation noise can perhaps maybe be heard in some extreme cases if dither isn't used, but only a fool would skip dithering so I wouldn't say that that is a problem anyways.