which remembers Shannon's theorem which is the basis fsampling=fmax*2.The argument is wrong anyway since sampling rate does not determine temporal resolution but bandwidth.
As I said, this comes from a complete ignorance of digital audio and signal processing fundamentals. These people think that digital audio is about connecting dots in straight lines, that samples have a temporal extent, that there are gaps between samples where information is lost, that there is an error if the sampling process doesn't match the signal peaks, and so on..
-
Welcome to ASR. There are many reviews of audio hardware and expert members to help answer your questions. Click here to have your audio equipment measured for free!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Updated Digital Audio Sampling vs. Perceived Quality OCT 15, 2022
- Thread starter Jim Shaw
- Start date
Actually you need more than twice the maximum frequency you want to encode. So fsampling > fmax*2fsampling=fmax*2.
i quote the Shannon theorem. nothing else.Actually you need more than twice the maximum frequency you want to encode. So fsampling > fmax*2
your quote is pedantic.
to perfect your education, fsample=fmax*2 is the frequency of nyquist 44.1 Shannon wrote: to perfectly reconstruct a digital signal, it must be sampled at twice the maximum frequency content, i.e. 22.05 kHz.
Last edited:
Your the one who keeps repeating how important math and science is… if you thinking is, details matter! Your theorem is just wrong, as can clearly be seen on Wikipedia:i quote the Shannon theorem. nothing else.
your quote is pedantic.
Specifically, you cannot for example sample a 22.05 kHz sine with 44.1 kHz sample rate for all phase configurations. Some will result in total silence. You can with 44.2 kHz though. Obviously there are other practical implications due to the need for reconstruction filters, but the theorem ignores these.
JayGilb
Major Contributor
Looks like he added some equipment to the stack behind him and he may have also dusted the knobs, so that a plus...
Really? Now that is a problem? It never is with all the other nonsense he spouts.
He thinks bit depth is only about dynamic range. He also thinks CD masters are recorded at 44.1 kHz?
Once again a load of nonsense, no proof, no controlled test, not even an explanation of the core “issue”.
- Thread Starter
- #26
I couldn't read the whole Paper as I'm not a member of the ASA, but I found the abstract interesting (and as you say, not altogether applicable). I continue to be interested in research findings as to human hearing sensitivities and timing resolution outside the conventional thought of 20 kHz limits (especially, in the time domain, regions of less than 50 micro sec., and due also to vagaries in the basilar membrane, meatus, tympanum, etc.).Often this study is cited:
It is however not exactly the right thing. It’s about timing differences between two ears. You can’t just extrapolate this to other use cases.
xnor
Active Member
- Joined
- Jan 12, 2022
- Messages
- 193
- Likes
- 209
Regarding pedantry, an interesting (or not) thing to know about sampling theory is that it supports both positive and negative frequencies through complex sinusoids.
In the complex plane (real from left to right, imaginary from bottom to top):
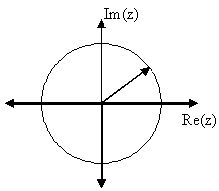
a positive-frequency complex sinusoid would rotate CCW in a circle, a negative one CW. Each positive and negative frequency from 0 up to Fs/2 Hz gets its own distinct point on the circle ... except for +/- Fs/2.
Both +Fs/2 and -Fs/2 get the same point (at 180° or z = -1), which can be viewed as aliasing. So you have to pick and agree on either using + or -Fs/2, but then you're fine.
Phase shift is simply rotation along that circle. So Fs/2 (180°, the leftmost point on the circle at z = -1 + 0i) with a phase shift of -90° would be rotated CW to 90° (topmost point on the circle) at z = 0 + 1i. Notice how the real part is then zero.
Real signals (like music) can be defined the same way except that they are a sum of two points mirrored over the real axis such that the imaginary parts cancel, leaving only the real part. So real signals rotate both in part CCW and CW and sum to points along the real number line.
This destroys the possibility to distinguish between positive and negative frequencies, or calculate magnitude or angle.
That means that reconstruction of a real sinusoid with a frequency of Fs/2 becomes limited to the case with 0° phase shift:
In the worst case (90° out of phase), the real part becomes zero so the sampling process would produce only zeroes and the reconstruction would result in silence.
In the best case (0° in phase), the real part matches the input signal.
In any intermediate case, the real part will be lower than the input's amplitude, cos(phase) to be precise, and the phase will be off by the input's phase shift.

In the complex plane (real from left to right, imaginary from bottom to top):
a positive-frequency complex sinusoid would rotate CCW in a circle, a negative one CW. Each positive and negative frequency from 0 up to Fs/2 Hz gets its own distinct point on the circle ... except for +/- Fs/2.
Both +Fs/2 and -Fs/2 get the same point (at 180° or z = -1), which can be viewed as aliasing. So you have to pick and agree on either using + or -Fs/2, but then you're fine.
Phase shift is simply rotation along that circle. So Fs/2 (180°, the leftmost point on the circle at z = -1 + 0i) with a phase shift of -90° would be rotated CW to 90° (topmost point on the circle) at z = 0 + 1i. Notice how the real part is then zero.
Real signals (like music) can be defined the same way except that they are a sum of two points mirrored over the real axis such that the imaginary parts cancel, leaving only the real part. So real signals rotate both in part CCW and CW and sum to points along the real number line.
This destroys the possibility to distinguish between positive and negative frequencies, or calculate magnitude or angle.
That means that reconstruction of a real sinusoid with a frequency of Fs/2 becomes limited to the case with 0° phase shift:
In the worst case (90° out of phase), the real part becomes zero so the sampling process would produce only zeroes and the reconstruction would result in silence.
In the best case (0° in phase), the real part matches the input signal.
In any intermediate case, the real part will be lower than the input's amplitude, cos(phase) to be precise, and the phase will be off by the input's phase shift.
Last edited:
Hi! Could you tell me please where I can learn about these open source alternatives?Oh, so you never get a thumbs up or replies? I had that happen on Oluv's gadgets. He didn't like me cutting into his revenue stream by suggesting free and open source alternatives to his patreon top-tier paywalled EQ presets for his earfun buds.
fieldcar
Addicted to Fun and Learning
Wavelet on Android or hesuvi with equalizer apo on windows. Though, a lot has happened since my post. It's best to just grab something that measures well according to asr, crinacle, or super reviews like one of the truthear or moondrop iems.Hi! Could you tell me please where I can learn about these open source alternatives?
GitHub - jaakkopasanen/AutoEq: Automatic headphone equalization from frequency responses
Automatic headphone equalization from frequency responses - jaakkopasanen/AutoEq
HeSuVi
Download HeSuVi for free. Headphone Surround Virtualizations for Equalizer APO. This tool imitates the 7.1 to binaural sound effect of many surround virtualizations by making use of Equalizer APO's convolution filter. Available are impulse response that were recorded with activated...
 sourceforge.net
sourceforge.net
Last edited:
Similar threads
- Replies
- 7
- Views
- 898
- Replies
- 14
- Views
- 1K
- Replies
- 8
- Views
- 1K

