INPUT WANTED: music tracks and methodology for testing audibility of group delay

[charlielaub]

As part of an effort of mine to develop and characterize some new crossover filters, I am looking for input on music tracks that I can use to test for the audibility of group delays that arise from the crossover filters.

Once I gather up a few test tracks (these should be limited to 10-20 seconds) I will do the following:
1. apply a range of filters that can be used in loudspeaker crossovers. The audio is split into 2 identical copies. One is passed through the LP filter and another is passed through the HP filter. These two are then summed, to mimic the summation "in air" of a loudspeaker's 2 drivers using this crossover. This will be saved as the processed version of the test track for crossover XYZ.
2. I will post audio files on my web site and then ask people to listen to them and rate them. I am not exactly sure of the best way to present the choice, but perhaps like this:
Three tracks: unprocessed original audio, audio processed with crossover A having low group delay, audio processed with crossover B that has high(er) group delay.
The tester first listens to the unprocessed track as many times as they would like, then they listen to the two processed tracks and are asked to rate which sounds better/cleaner/whatever.
I collect these poll results and after some time (a month?) present the results.

If this testing format is not ideal, please suggest a better one.

The problem that I see is that the overachiever out there who wants to score 100% could download the audio and then do some analysis of the group delay profile, therefore "cheating" by obtaining the correct answer to the "test". I'm not sure this could be done with a music file or not, but if you know of a way to thwart this sort of cheating please let me know. It would be nice to get some honest results back.

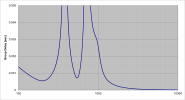
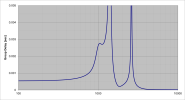
One motivator for this sort of testing is that I have developed a new "family" of crossover filters that have a very steep transition band but limited maximum attenuation, which I created from elliptical filters via optimization to reduce group delay, improve LP+HP summation to reduce ripple, etc. These steeper filters do have group delay that is elevated, but I consulted the published literature in psycho-acoustics to see where the threshold of audibility lies, and made sure that the crossovers remained below those levels for all audio frequencies. Since there is a camp that elevates linear phase type filters, I would like to throw down this challenge to see if, with music signals, people can actually detect group delay peaking, etc. (phase distortion) and at what level. It can't be 100% scientific via this sort of approach, but would be at least some real data.

Please share your thoughts on this experiment and its deisgn. If someone has experience with these sorts of polls and how to set them up, I would love to hear about it.

Also, please suggest some tracks that might highlight group delay non-linearities. Supposedly our hearing is most sensitive to strong transients like click sounds and when using headphones. I want to focus more on music and not synthetic signals, nor something like only two drumsticks or woodblocks being hit together. At the other extreme, no mostly-continuous tones like organ music either. I could possibly present a few (3 or 4) different tracks for each test. Your input is appreciated.

 

[charlielaub]

Here is a link to the published review paper from Liski et al that I used as a basis for limiting the maximum allowed group delay. See Figure 1, second page:

https://acris.aalto.fi/ws/portalfiles/portal/66449704/Audibility_of_Group_Delay_Equalization.pdf

In addition to the lit review they also present some research and their test signals. Two signals were synthetic in nature and the other two were "Castanets" and "High Hat". The "real world" sounds have a higher threshold of group delay audibility (e.g. see Figure 11).

 

[Roland68]

The tester must not know what he is listening to, i.e. edited or unedited.
You must reshuffle each round and provide answers to choose from.
Ideally, there would be three rounds of 3 tracks each, with no repetitions, where the only possible answer is better or worse than the previous one.
So you have the 3 tracks rated 3 times in different orders.

 

[somebodyelse]

It seems similar to Archimago's recent DAC blind ranking if you allow that people may prefer the filtered signal to the original. The results cover the analysis. With only a single ranking per person it doesn't demonstrate that an individual could consistently give the same ranking. Your use of multiple sample tracks counters that somewhat. The simple test procedure probably helps with the number of participants though - some probably wouldn't have bothered if it involved rounds of ABX tests or similar. The simple ranking also means participants don't need specific testing software which may not be available for all platforms.

 

[voodooless]

Three tracks: unprocessed original audio, audio processed with crossover A having low group delay, audio processed with crossover B that has high(er) group delay.

So how do you know that you're actually testing for group delay differences, and not any difference resulting from the frequency response change?

You'll need to separate the two things, which can be done by using FIR filters. You can add group delay without changing the frequency response.

 

[charlielaub]

So how do you know that you're actually testing for group delay differences, and not any difference resulting from the frequency response change?

You'll need to separate the two things, which can be done by using FIR filters. You can add group delay without changing the frequency response.

The highpass and lowpass filter crossover outputs are recombined to generate the test signal, so it should be like the input signal plus the addition of a group delay (all-pass) response. The frequency response is unchanged (not exactly for the DFE filters, but close). So the change can be attributed to the addition of non-uniform, frequency-dependent group delay. I am testing for the ability of people to detect whether the crossover changes the signal compared to the original, so if there is some influence of small frequency response deviations that would also be useful to know.

BTW I was considering using a 1kHz crossover frequency. The ear is sensitive in this frequency region and peaking in the group delay happens close to Fc.

 

[voodooless]

The highpass and lowpass filter crossover outputs are recombined to generate the test signal, so it should be like the input signal plus the addition of a group delay (all-pass) response.

Note that part of the group delay effect will be canceled out by this due to the roughly mirrored phase responses of the filters when you combine them again. You can use asymmetric filters or delay one of them to make the effect bigger, but you'll need to be careful that the summed spectrum is flat enough.

 

[charlielaub]

Note that part of the group delay effect will be canceled out by this due to the roughly mirrored phase responses of the filters when you combine them again. You can use asymmetric filters or delay one of them to make the effect bigger, but you'll need to be careful that the summed spectrum is flat enough.

There is a group delay of the crossover summation. It has finite DC delay, possibly some peaking at Fc, and decays to zero at high frequencies. It is the same for all "analog style" (e.g. also IIR digital) crossover realizations that are all-pass in nature. The GD of the crossover sum looks like this:

There is no need to do anything except pass the audio through the HP and LP filters and then recombine them via summation. The all-pass like response means the FR is flat but you get some GD added due to the phase response of the filters.

 

[voodooless]

The GD of the crossover sum looks like this:

This is not the group delay of the sum, this is the group delay of the low pass only, see the source of the image:

https://www.eeweb.com/filter-topology-chebyshev-butterworth-and-bessel/

 

[charlielaub]

This is not the group delay of the sum, this is the group delay of the low pass only, see the source of the image:

https://www.eeweb.com/filter-topology-chebyshev-butterworth-and-bessel/

True, but trust me the group delay of the sum looks just like that too. I had to grab a representative image and on the web no one is showing that for the crossover, just for LP filters because that is often the primary use.

Here is an image of group delay of the crossover sum taken from my very own modeling tools. It's an LR4 crossover. All the features I described are there.

 

[voodooless]

Here is an image of group delay of the crossover sum taken from my very own modeling tools. It's an LR4 crossover. All the features I described are there.

Can you plot the group delays of the LP and HP in here as well? Would like to see how they combine.

 

[charlielaub]

Here is one of my DFE filters. The FR of the LP filter and the GD of the crossover sum are shown below.

 

[charlielaub]

Can you plot the group delays of the LP and HP in here as well? Would like to see how they combine.

Sure. For the same filter above and not weighted by amplitude, here are the individual LP and HP group delays vs frequency. Note different y-axis scale because the peaking is higher.

 

[voodooless]

Note different y-axis scale because the peaking is higher.

Yeah, exactly. That was my whole point. The sum has a vastly smaller group delay than each half. As long as the resulting GD is in the range that you want for your test, you should be fine. Note though that that 7th order filter isn't symmetrical with those deep nulls, and the stopband is poor. I'm not sure if you can discount this from having any audible influence.

 

[charlielaub]

Yeah, exactly. That was my whole point. The sum has a vastly smaller group delay than each half. As long as the resulting GD is in the range that you want for your test, you should be fine. Note though that that 7th order filter isn't symmetrical with those deep nulls, and the stopband is poor. I'm not sure if you can discount this from having any audible influence.

Well, not exactly. What I plotted is the group delay of the response regardless of the magnitude of the response. In the crossover sum, the group delay of the sum is made up of the "weighted" (by the amplitude) contribution from each LP or HP response. So to compare apples to apples I would need to calculate the "amplitude weighted" group delay for each individual response. Unfortunately I do not have those plots at hand, but you probably get the idea. Specifically, the first GD peak above Fc for e.g. the LP filter corresponds to the lowest frequency notch in the response, so the amplitude there is very low.

I'm not sure what you mean when you say "the 7th order filter isn't symmetrical". Also, what is so "poor" about the stopband? This is for loudspeaker crossovers. Attenuation of 45dB (in this case) is excellent and enough to keep the stopband from causing problems with the passband of the other filter. Can you expand on those comments?

 

[voodooless]

I'm not sure what you mean when you say "the 7th order filter isn't symmetrical".

Well, it's isn't symetrical in the sense that the nulls are indeed present in both LP and HP, but not at the same spots. They will not even out.

Also, what is so "poor" about the stopband? This is for loudspeaker crossovers. Attenuation of 45dB (in this case) is excellent and enough to keep the stopband from causing problems with the passband of the other filter. Can you expand on those comments?

The Butterworth filter achieves much better attenuation eventually 45 dB attenuation is relatively low in general. It may be okay for a speaker filter but as a semi-brick wall digital filter, it's not very impressive The Butterworth filter will also have better group delay because of the smooth transition. Either way, a 7th-order filter isn't super realistic for a speaker crossover either. Most passive ones will be 2nd to 4th order. Active ones may be of higher order, but that's not always a good idea.

 

[charlielaub]

Well, it's isn't symetrical in the sense that the nulls are indeed present in both LP and HP, but not at the same spots. They will not even out.

I still have no idea what you are concerned about. The HP filter is just the LP filter "flipped" about Fc. The nulls are in the stopband, they do not "cancel" anything nor are they intended to. What you are saying makes no sense at all.

The Butterworth filter achieves much better attenuation eventually 45 dB attenuation is relatively low in general. It may be okay for a speaker filter but as a semi-brick wall digital filter, it's not very impressive The Butterworth filter will also have better group delay because of the smooth transition. Either way, a 7th-order filter isn't super realistic for a speaker crossover either. Most passive ones will be 2nd to 4th order. Active ones may be of higher order, but that's not always a good idea.

Sorry that I was not more clear, since I did not post a link to my paper (in the September issue of AudioXpress). These filters are meant for loudspeaker crossovers, not for brick wall filtering like elliptical and FIR filters. Please keep that in mind when you comment on the responses. And it is not really feasibly to implement it as a passive crossover, it is for line-level applications or IIR DSP. I don't find your concerns valid, honestly.

We are taking this thread way off course. Maybe you could PM me if you want to continue to discuss these issues.

IN the meantime I am looking for input on tracks to use for testing, and testing methodologies for testing the audibility of group delay in loudspeaker crossovers. Thanks.

 

[Tranquility Bass]

Well, it's isn't symetrical in the sense that the nulls are indeed present in both LP and HP, but not at the same spots. They will not even out.

The Butterworth filter achieves much better attenuation eventually 45 dB attenuation is relatively low in general. It may be okay for a speaker filter but as a semi-brick wall digital filter, it's not very impressive The Butterworth filter will also have better group delay because of the smooth transition. Either way, a 7th-order filter isn't super realistic for a speaker crossover either. Most passive ones will be 2nd to 4th order. Active ones may be of higher order, but that's not always a good idea.

He's designing crossover filters, not reconstruction filters for DAC's or anti-aliasing filters for ADC's

 

[Tranquility Bass]

Here is one of my DFE filters. The FR of the LP filter and the GD of the crossover sum are shown below.

So we are on the same page which filter is this from your AE article ??

 

[617]

Charlie, first of all it's good to see you posting here and still meddling with speakers. I've been following you for a long time now.

My expectation, which I suspect you share, is that listeners will probably not be able to detect, and certainly won't be able to articulate a preference between samples. It will be interesting if I am wrong.

However, won't real world speakers demonstrate different off axis behavior with differing crossovers? It seems as if this would be a much more significant difference than what we are scrutinizing here.