This is an article I wrote for Widescreen Review Magazine which came out a couple of years ago. This is a revised and updated version.
----
Audibility of Small Distortions
By Amir Majidimehr
Spend five minutes in any audio forum and you immediately run into food fights over audibility of small distortions. Debates rage on forever on differences between amplifiers, cables, DACs, etc. I do not have high hopes of settling those debates. But maybe I can chart a fresh way through the maze that partially answers the question.
The challenge here is that in some of these cases we can show measurable distortion in the audio band. Therefore we cannot rule out easily that there are no differences. Yes, we can resort to listening tests but who wants to go and perform a rigorous listening test just to buy a new AVR or DAC? It is not like there are people who routinely perform these tests for us. Shouldn’t we have a way to evaluate the performance of these systems just from their specifications? There may be.
Let’s look at a trivial example. If I filter out the audio spectrum above 10 KHz, just about everyone can detect that I have changed the sound. Even the most staunch advocates of “give me a blind listening test or else” would accept that we don’t need to perform a blind test to accept that such a system has audible problems. So there can be specifications which trump the need to perform listening tests.
Given the advances in our audio systems, such easy way outs don’t exist for the most part. In digital systems for example the distortion can be dependent on what the system is doing, or what content is being played. Imagine having a distortion that pops up if the rightmost digits in your audio sample are alternating 0 and 1s but not any other sequence. For such a distortion to be audible we would have to hit on this specific sequence or we would be testing the wrong thing. This is not hard if you know what I just told you. But without that knowledge which is the typical case, you would be lost in the wind trying to find source material that would trigger these sequences.
Let’s take a short detour into acoustics and examine small distortions there and see if they lend us some insight here, namely, the case of resonances in speakers and rooms.
Audibility of Resonances
A resonance is an attribute of a system where it contributes to the amplitude of the source signal, causing the frequency response to have peaks in it. Take a look at the following three resonances:
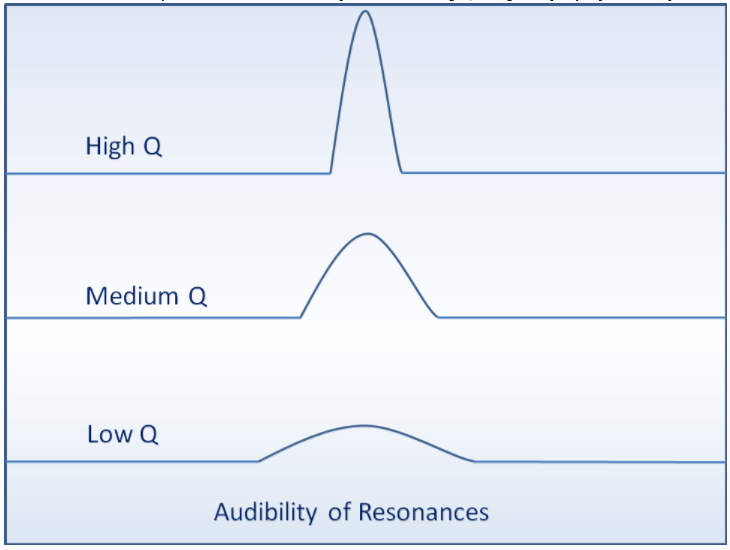
The “Q” indicates how steep the resonance is in frequency domain. In time domain, the higher the Q, the more “ringing” the system has. Ringing means that a transient signal (think of a spike) will create ripples that go on after it disappears. An ideal system would reproduce that transient with zero ringing. The higher the Q of a resonance, the more ringing the system has.
Reading what I just wrote, if I asked which one of the above resonances is more audible, you will likely say High Q. It seems natural that it has the highest amplitude change and more time domain impact. Yet listening tests show the opposite to be true! The Low Q is more audible.
How can that be? Well, it has to do with statistics. A Low Q resonance spans a wider set of frequencies. That increases the chances that some tone in our source content hits it and therefore will be reproduced at the wrong level. The narrow resonance can do more damage but the probability of us catching it in the act is lower because fewer tones energize it.
Listening tests conducted by Toole and Olive show that we hear variations as low as 0.5 decibels in Low Q resonances. This makes a mockery of the typical industry specification of +-3 dB being good enough for speakers. Clearly if 0.5 dB is audible, +-3 dB represents a huge amount of audible variation from our target neutral reproduction of our source material.
With that background now let’s look at a more challenging situation, namely jitter in digital systems.
Audibility of Jitter
Readers of my past articles are probably familiar with the concept of jitter distortion in digital systems. As a quick review, jitter is a variation in the speed with which we output our digital samples (so called DAC clock). The deviations from the ideal timing generate spikes on either side of our source frequencies. Here is an example of jitter at a frequency of 2.5 KHz acting on a 10 KHz source signal:
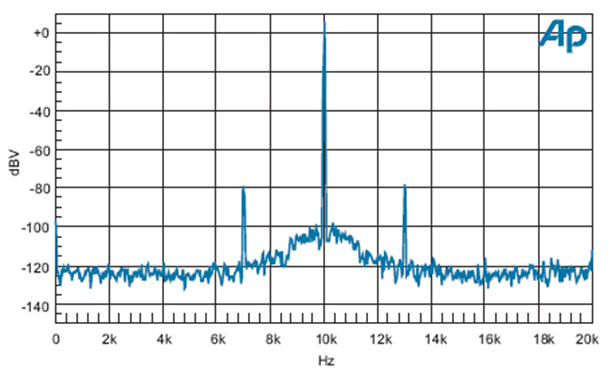
Jitter “amplitude” is specified in units of nanoseconds or picoseconds as appropriate. Nanosecond is a billionth of a second. Picosecond is a trillionth of a second or 10 to the power of -12. The above graph shows a jitter level of 7.6 nanoseconds with a profile of a sine wave creating those distortion spikes on either side of our source frequency.
So how do we determine if those spikes are audible? The first step in that is to review listening tests by Bell Labs researchers Fletcher and Munson who investigated our hearing sensitivity as a function of level and frequency as represented in this graph:
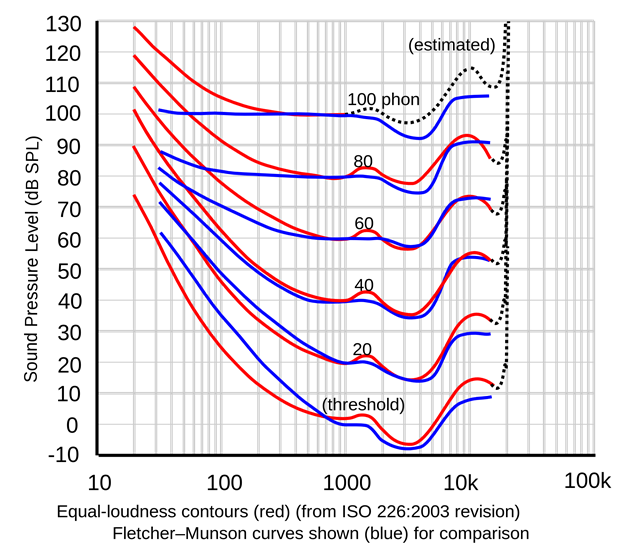
For the purposes of this article, we only care about the bottom one labeled “threshold.” This is the lowest audible level (for the average population) of a tone plotted on a per frequency basis. It becomes very clear from this research that our hearing system is far more sensitive in the mid-range frequencies of roughly 2 to 4 KHz. If there is going to be an audible distortion that is where it is going to be.
Pictorially, this is what our distortion needs to do to reach the level of audibility:
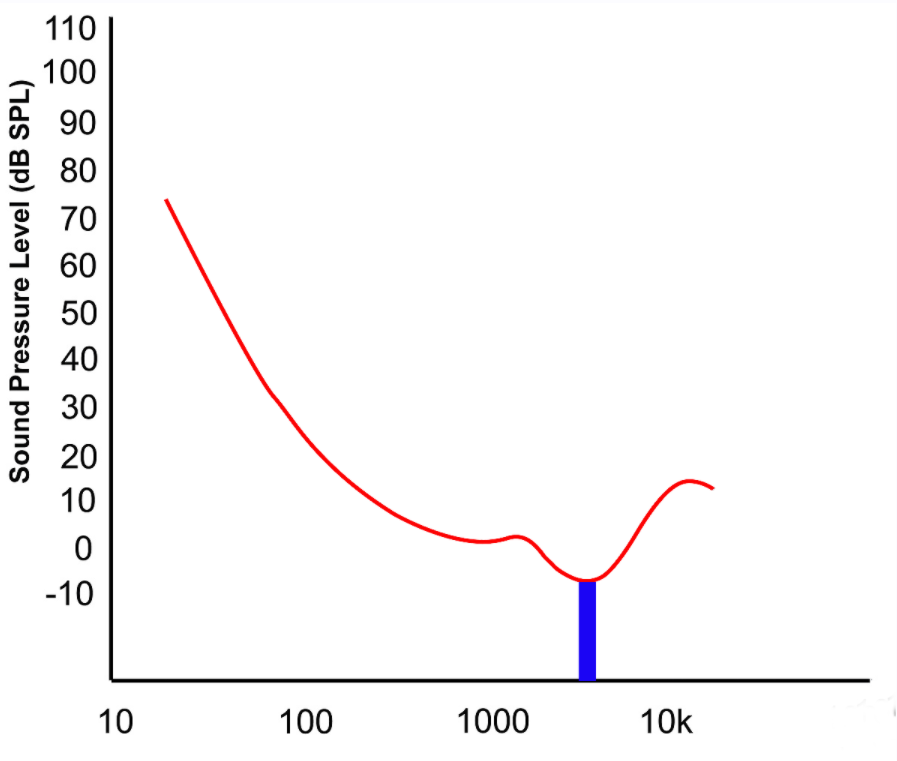
The trick with jitter is that the higher the frequency, the higher the distortion products created for identical amount of jitter! This should make intuitive sense in that the higher our music frequency, the higher ratio the timing error will represent. Assuming a worst case scenario of a full amplitude 20 KHz signal, it takes about 30 picoseconds or 30E-12 of timing error for the distortion to exceed threshold of hearing if it lands in that most sensitive hearing range.
Fortunately, we don’t have full amplitude 20 KHz signals in our music or we would have lots of blown tweeters, amplifiers that may oscillate/shut down, etc. The biggest help we have here is something called Perceptual Masking in psychoacoustics science. So let’s get into that.
Effect of Masking
Masking is a rather simple concept: it says that if something loud is playing, frequencies near it may be less or not audible at all. Take a look at these two distortion products in red and blue with equal amplitude relative to our source signal:
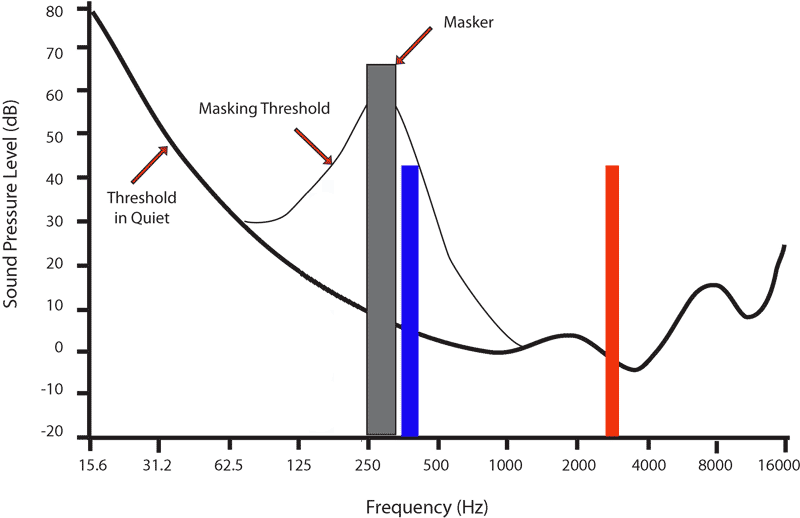
The blue distortion is masked by the shadow of the gray source signal (called “masker” above). In that sense it is likely inaudible despite its high amplitude. The red distortion spike on the other is extremely audible since it not only is outside of the masking area of our source signal but also happens to land where our hearing system is most sensitive.
Since we have no control over our source content, i.e. music we play, it is impossible to assert that across all source material masking would help make the distortion inaudible. The equipment distortion could very well become audible in the right circumstances.
Put another way, just like our resonance situation, whether these distortions are audible is a matter of statistics. This means that we could run a number of blind tests and get negative outcomes for audibility not because the distortion is not audible in the absolute, but because we didn’t find the right source material to excite it the right way.
A proper listening test for jitter then starts with using the right material where masking is not constantly covering the distortion. We do this in audio compression where the clips we select reduce the impact of masking as to make it easier to hear codec distortion. Unfortunately in the few jitter listening tests that have gone on, the selection of music has not been made this way.
Of note, picking “audiophile music” is the wrong approach here. There is no telling if audiophile music is more revealing this way. None of the codec test music for example falls in this category.
There is something we can learn here though by inverting this equation and arriving at something more absolute: if our distortion is below the threshold of hearing then we can sleep easy knowing that it is inaudible across all content. Using Hawksford and Dunn research for example, a DAC that generates less than 20 picoseconds would be transparent to its source assuming jitter is the only distortion we are worried about.
This gets us to where we wanted to be, i.e. a specification that tells us that we have achieved the right target fidelity level. Yes, this likely sets too high a bar relative to our ability to hear such non-linear distortions, or hear it in our content. So if you like, you can target higher values. But don’t go too far. There is no way to build a credible case that thousands of picoseconds of jitter as we usually get over HDMI for example is inaudible. The analysis I just provided shoots way too many holes in that line of reasoning. My personal target is a few hundred picoseconds.
References
"Sound Reproduction: The Acoustics and Psychoacoustics of Loudspeakers and Rooms," Dr. Floyd Toole, 2008 [book]
“Is the AESEBU / SPDIF Digital Audio Interface Flawed? Chris Dunn and Malcom Hawksford, Audio Research Group, Department of Electronic Systems Engineering, University of Essex, AES convention paper, 1992.
Amir Majidimehr is the founder of audio/video/integration/automation company, Madrona Digital (madronadigital.com). Prior to that, he spent over 30 years in the computer and broadcast/consumer video industries at leading companies from Sony to Microsoft, always pushing to advance the state-of-the-art in delivery and consumption of digital media. Technologies developed in his teams are shipped in billions of devices from leading game consoles and phones to every PC in the world and are mandatory in such standards as Blu-ray. He retired as Corporate VP at Microsoft in 2007 to pursue other interests, including advancing the way we interconnect devices in our homes for better enjoyment of audio/video content.
----
Audibility of Small Distortions
By Amir Majidimehr
Spend five minutes in any audio forum and you immediately run into food fights over audibility of small distortions. Debates rage on forever on differences between amplifiers, cables, DACs, etc. I do not have high hopes of settling those debates. But maybe I can chart a fresh way through the maze that partially answers the question.
The challenge here is that in some of these cases we can show measurable distortion in the audio band. Therefore we cannot rule out easily that there are no differences. Yes, we can resort to listening tests but who wants to go and perform a rigorous listening test just to buy a new AVR or DAC? It is not like there are people who routinely perform these tests for us. Shouldn’t we have a way to evaluate the performance of these systems just from their specifications? There may be.
Let’s look at a trivial example. If I filter out the audio spectrum above 10 KHz, just about everyone can detect that I have changed the sound. Even the most staunch advocates of “give me a blind listening test or else” would accept that we don’t need to perform a blind test to accept that such a system has audible problems. So there can be specifications which trump the need to perform listening tests.
Given the advances in our audio systems, such easy way outs don’t exist for the most part. In digital systems for example the distortion can be dependent on what the system is doing, or what content is being played. Imagine having a distortion that pops up if the rightmost digits in your audio sample are alternating 0 and 1s but not any other sequence. For such a distortion to be audible we would have to hit on this specific sequence or we would be testing the wrong thing. This is not hard if you know what I just told you. But without that knowledge which is the typical case, you would be lost in the wind trying to find source material that would trigger these sequences.
Let’s take a short detour into acoustics and examine small distortions there and see if they lend us some insight here, namely, the case of resonances in speakers and rooms.
Audibility of Resonances
A resonance is an attribute of a system where it contributes to the amplitude of the source signal, causing the frequency response to have peaks in it. Take a look at the following three resonances:
The “Q” indicates how steep the resonance is in frequency domain. In time domain, the higher the Q, the more “ringing” the system has. Ringing means that a transient signal (think of a spike) will create ripples that go on after it disappears. An ideal system would reproduce that transient with zero ringing. The higher the Q of a resonance, the more ringing the system has.
Reading what I just wrote, if I asked which one of the above resonances is more audible, you will likely say High Q. It seems natural that it has the highest amplitude change and more time domain impact. Yet listening tests show the opposite to be true! The Low Q is more audible.
How can that be? Well, it has to do with statistics. A Low Q resonance spans a wider set of frequencies. That increases the chances that some tone in our source content hits it and therefore will be reproduced at the wrong level. The narrow resonance can do more damage but the probability of us catching it in the act is lower because fewer tones energize it.
Listening tests conducted by Toole and Olive show that we hear variations as low as 0.5 decibels in Low Q resonances. This makes a mockery of the typical industry specification of +-3 dB being good enough for speakers. Clearly if 0.5 dB is audible, +-3 dB represents a huge amount of audible variation from our target neutral reproduction of our source material.
With that background now let’s look at a more challenging situation, namely jitter in digital systems.
Audibility of Jitter
Readers of my past articles are probably familiar with the concept of jitter distortion in digital systems. As a quick review, jitter is a variation in the speed with which we output our digital samples (so called DAC clock). The deviations from the ideal timing generate spikes on either side of our source frequencies. Here is an example of jitter at a frequency of 2.5 KHz acting on a 10 KHz source signal:
Jitter “amplitude” is specified in units of nanoseconds or picoseconds as appropriate. Nanosecond is a billionth of a second. Picosecond is a trillionth of a second or 10 to the power of -12. The above graph shows a jitter level of 7.6 nanoseconds with a profile of a sine wave creating those distortion spikes on either side of our source frequency.
So how do we determine if those spikes are audible? The first step in that is to review listening tests by Bell Labs researchers Fletcher and Munson who investigated our hearing sensitivity as a function of level and frequency as represented in this graph:
For the purposes of this article, we only care about the bottom one labeled “threshold.” This is the lowest audible level (for the average population) of a tone plotted on a per frequency basis. It becomes very clear from this research that our hearing system is far more sensitive in the mid-range frequencies of roughly 2 to 4 KHz. If there is going to be an audible distortion that is where it is going to be.
Pictorially, this is what our distortion needs to do to reach the level of audibility:
The trick with jitter is that the higher the frequency, the higher the distortion products created for identical amount of jitter! This should make intuitive sense in that the higher our music frequency, the higher ratio the timing error will represent. Assuming a worst case scenario of a full amplitude 20 KHz signal, it takes about 30 picoseconds or 30E-12 of timing error for the distortion to exceed threshold of hearing if it lands in that most sensitive hearing range.
Fortunately, we don’t have full amplitude 20 KHz signals in our music or we would have lots of blown tweeters, amplifiers that may oscillate/shut down, etc. The biggest help we have here is something called Perceptual Masking in psychoacoustics science. So let’s get into that.
Effect of Masking
Masking is a rather simple concept: it says that if something loud is playing, frequencies near it may be less or not audible at all. Take a look at these two distortion products in red and blue with equal amplitude relative to our source signal:
The blue distortion is masked by the shadow of the gray source signal (called “masker” above). In that sense it is likely inaudible despite its high amplitude. The red distortion spike on the other is extremely audible since it not only is outside of the masking area of our source signal but also happens to land where our hearing system is most sensitive.
Since we have no control over our source content, i.e. music we play, it is impossible to assert that across all source material masking would help make the distortion inaudible. The equipment distortion could very well become audible in the right circumstances.
Put another way, just like our resonance situation, whether these distortions are audible is a matter of statistics. This means that we could run a number of blind tests and get negative outcomes for audibility not because the distortion is not audible in the absolute, but because we didn’t find the right source material to excite it the right way.
A proper listening test for jitter then starts with using the right material where masking is not constantly covering the distortion. We do this in audio compression where the clips we select reduce the impact of masking as to make it easier to hear codec distortion. Unfortunately in the few jitter listening tests that have gone on, the selection of music has not been made this way.
Of note, picking “audiophile music” is the wrong approach here. There is no telling if audiophile music is more revealing this way. None of the codec test music for example falls in this category.
There is something we can learn here though by inverting this equation and arriving at something more absolute: if our distortion is below the threshold of hearing then we can sleep easy knowing that it is inaudible across all content. Using Hawksford and Dunn research for example, a DAC that generates less than 20 picoseconds would be transparent to its source assuming jitter is the only distortion we are worried about.
This gets us to where we wanted to be, i.e. a specification that tells us that we have achieved the right target fidelity level. Yes, this likely sets too high a bar relative to our ability to hear such non-linear distortions, or hear it in our content. So if you like, you can target higher values. But don’t go too far. There is no way to build a credible case that thousands of picoseconds of jitter as we usually get over HDMI for example is inaudible. The analysis I just provided shoots way too many holes in that line of reasoning. My personal target is a few hundred picoseconds.
References
"Sound Reproduction: The Acoustics and Psychoacoustics of Loudspeakers and Rooms," Dr. Floyd Toole, 2008 [book]
“Is the AESEBU / SPDIF Digital Audio Interface Flawed? Chris Dunn and Malcom Hawksford, Audio Research Group, Department of Electronic Systems Engineering, University of Essex, AES convention paper, 1992.
Amir Majidimehr is the founder of audio/video/integration/automation company, Madrona Digital (madronadigital.com). Prior to that, he spent over 30 years in the computer and broadcast/consumer video industries at leading companies from Sony to Microsoft, always pushing to advance the state-of-the-art in delivery and consumption of digital media. Technologies developed in his teams are shipped in billions of devices from leading game consoles and phones to every PC in the world and are mandatory in such standards as Blu-ray. He retired as Corporate VP at Microsoft in 2007 to pursue other interests, including advancing the way we interconnect devices in our homes for better enjoyment of audio/video content.
Last edited:
