Visualizing 8x oversampling of 4 bit DAC + 5 bit

[mike7877]

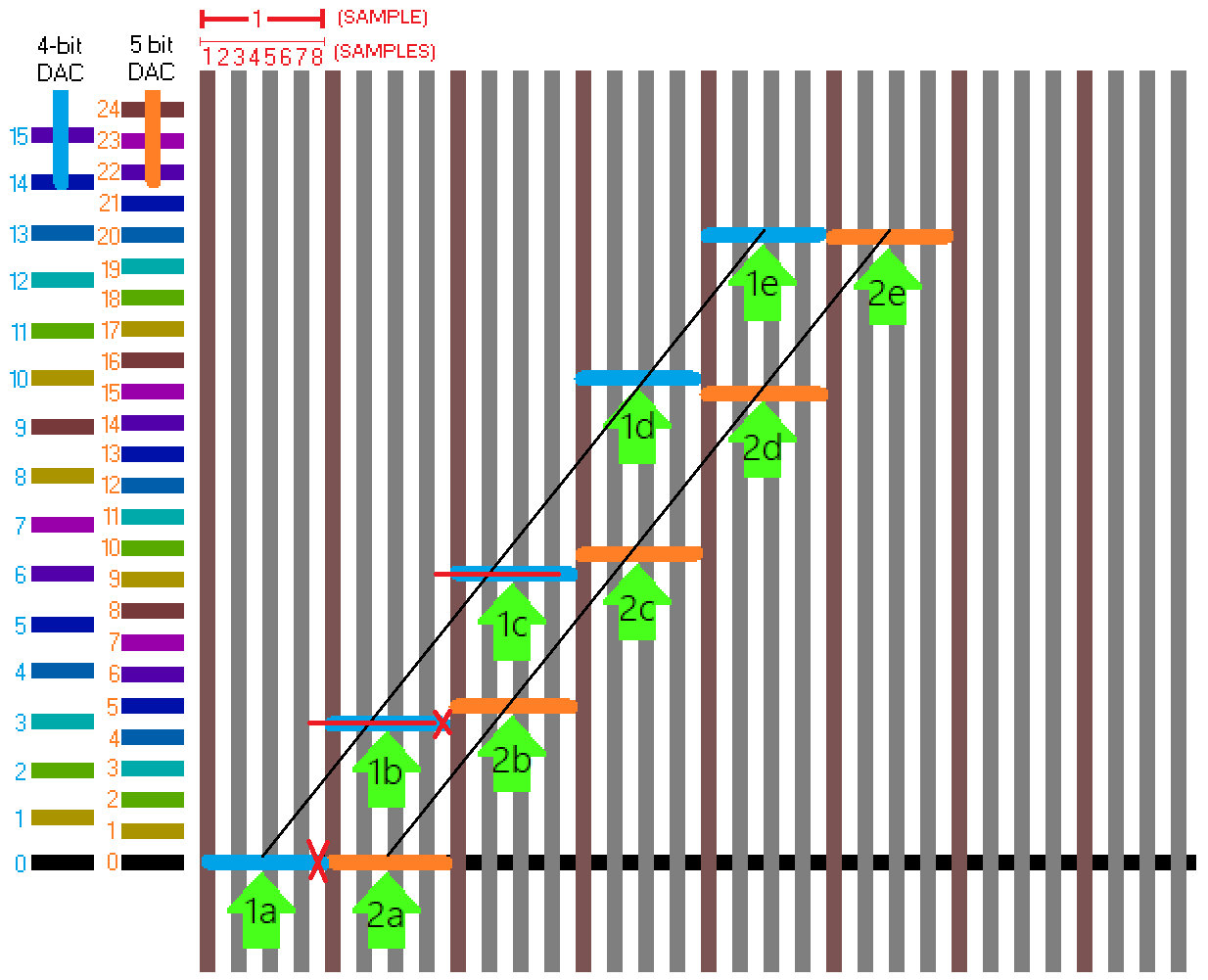
I spent some time in paint to contrast a 4 and 5 bit DAC doing the same thing, then the 4 bit DAC with 8x oversampling (increasing its resolution by 1.5 bits, woo!)

Did I do it right?

(yes, it's all+ lol... this ain't music! Just a rising voltage...)

It took me a little while to think over how I was going to do this, then arranging it, counting the pixels for proper spacing so it actually made a bit of sense... (the 5 bit DAC was the perfect device to capture the rising voltage, and perfectly in phase, too! If my brain didn't let me down I probably would've done 5 and 6 bit and just not shown the bottom half... NEXT TIME! lol)

I labelled things so that it's easier to discuss, get clarification, or point out problems

In case it's not obvious, the red-brown vertical lines are the 1x sample rate, and the brown, white, grey, white, grey, white, grey, white are 1, 2, 3, 4, 5, 6, 7, 8 samples for the 8x.
The blue lines are the 4 bit DAC originally, and the thin red lines over the blue lines are the 8x oversample (corrected) position. When there are no red lines, the blue lines are the red lines, and when the red x is over blue line, it's because the red line has taken its place.
(BTW the black lines are exact to the pixel precision - starting in the same spot (top center) in 1a/2a, and finishing in the top center of 2e, but not 1e, because the 4 bit DAC's 13th step is slightly higher than the 5 bit DAC's 20th)


Is this also how delta-sigma DACs work? Just running at many many many MHz?
Or is this a horrible failing - go back to grade 1 and stay there for 2 years Michael. No recess, no lunch, and 2 hours of homework for every hour you were in school during the day!

 

[voodooless]

If you didn’t use any math for the new samples, you didn’t do it right

Also, where are the original samples, where is the original waveform? I don’t see them…

 

[mike7877]

If you didn’t use any math for the new samples, you didn’t do it right

Also, where are the original samples, where is the original waveform? I don’t see them…

The original is the black lines. It's not meant to be mathematically exact, just to look generally like the process which occurs. I did space everything properly, so best fit should be correct

edit: I should've drawn the red lines at the top of the blue lines, not in the middle to show how it's centered more accurately. Just pretend it's higher!

(and whatever else mgiht be wrong with it lol)

 

[voodooless]

The original is the black lines

Well, then the samples at the brown lines should be measured there, but clearly they are not.

Also, remember that a multibit DS DAC will output PWM, not a PCM signal. The oversampling stage will probably use 32 or 64 bits.

 

[mike7877]

Well, then the samples at the brown lines should be measured there, but clearly they are not.

Also, remember that a multibit DS DAC will output PWM, not a PCM signal. The oversampling stage will probably use 32 or 64 bits.

I guess I titled this wrong - I'm not after what the output from the DAC looks like on a 'scope, but what's happening to the information as it's being 8x oversampled. Basically how it would be stored as PCM as it was resampled

 

[voodooless]

Well, my first paragraph still holds.

It's not meant to be mathematically exact, just to look generally like the process which occurs.

The process is pure math. Doing it without math is counterproductive.

 

[AnalogSteph]

There is no oversampling without a digital filter. Take a look at the datasheets of, say, some classic NPC jobs like the SM5803 (or the OG, the Philips SAA7030). At their core they consist of a cascade of zero insertion and half-band filter stages, doubling fs every time. You could technically insert 7 zeroes at once and do the filtering in one go, it would just increase filter complexity a lot. You save half the coefficients with half-band filters, plus the higher you go, the less steep the filter needs to be to keep the aliases at bay. Oh yeah, and during final requantization they apply shaped dither as well. That's a whole lotta math.

BTW, 4 and 5 bits is still too much for illustration. Why not 3 and 4 bits, or even 2 and 3?

 

[solderdude]

The advantage of 5 bits over 4 bits in an DS DAC is just that the quantization noise is a bit lower in level (before it goes into the analog post filter)
When this is combined with higher switching frequencies you can lower the noise floor a little and increase the theoretical resolution.
I say theoretical as the real world noise floor is already higher than the resolution of DS DACs (has nothing to do with the amount of bits)
That noise is pushed above the audible band anyway.

 

[mike7877]

There is no oversampling without a digital filter. Take a look at the datasheets of, say, some classic NPC jobs like the SM5803 (or the OG, the Philips SAA7030). At their core they consist of a cascade of zero insertion and half-band filter stages, doubling fs every time. You could technically insert 7 zeroes at once and do the filtering in one go, it would just increase filter complexity a lot. You save half the coefficients with half-band filters, plus the higher you go, the less steep the filter needs to be to keep the aliases at bay. Oh yeah, and during final requantization they apply shaped dither as well. That's a whole lotta math.

BTW, 4 and 5 bits is still too much for illustration. Why not 3 and 4 bits, or even 2 and 3?

The advantage of 5 bits over 4 bits in an DS DAC is just that the quantization noise is a bit lower in level (before it goes into the analog post filter)
When this is combined with higher switching frequencies you can lower the noise floor a little and increase the theoretical resolution.
I say theoretical as the real world noise floor is already higher than the resolution of DS DACs (has nothing to do with the amount of bits)
That noise is pushed above the audible band anyway.

Say the black line is the original representation of the voltage increasing.
The 2a/b/c/d/e samples ars the perfect representation of it (ie. when the 5 bit DAC is run with its filter, the black line is reconstructed perfectly)

The 1a/b/c/d/e samples are the 4 bit DAC doing its best to follow the black line with 8x oversampling.

In the case of the 4 bit samples, they are not perfectly representative of the original waveform, but the closest approximation with 8x oversampling

I didn't do enough 'splainin lol.

You see, the 4 bit 8x oversample example is essentially trying to replicate the black line running through it, but when the samples are finally put through the optimal freconstruction filter for the task, it will still not be exactly the same as the 5 bit DAC (at the very least I assume there would be phase differences, even if frequency and amplitude are represented accurately with the oversampling and filtering.

Oh, and I just realised.....
I screwed up the vertical axis because in the beginning I made each DAC's peak +1 its actual value, and I didn't stretch the 4 bit DAC's 15 to the same position as 24 (I forgot... it would've been a lot of moving by x pixels in paint if I didn't!) Anyway, with this error it makes my best fit and samples incorrect.


The number of samples and their rough position is what I was trying to represent when a bit is lost and samples are added. The example I chose to make is losing 1 bit and 8x oversampling.

Pretend I didn't forget to line up 15 with 24: is this be a good way of mentally visualizing the process that's done in DACs when best fit/averaging is used for oversampling with less bits? I know there's math and different filtering techniques to get more from less and optimize efficiency and and and and. But for the most basic picture to stick all that shite to and around from wherever it comes/has come from, whenever it comes (or doesn't).

 

[mike7877]

Oh, they're also supposed to be resistor switched 4 and 5 bit DACs, like AK4499EX

 

[DonH56]

Oversampling without delta-sigma modulation yields about 0.5 bit for each doubling of the sampling rate. Add 1 bit for each order in the modulator, e.g. a 4th-order modulator yields about 5.5 bits in SNR for each doubling of the sampling rate.

Adding bits to the DAC adds ~6 dB/bit in SNR regardless of the sampling rate.

 

[AnalogSteph]

Oversampling without delta-sigma modulation yields about 0.5 bit for each doubling of the sampling rate. Add 1 bit for each order in the modulator, e.g. a 4th-order modulator yields about 5.5 bits in SNR for each doubling of the sampling rate.

That's handy and makes sense (noise shaping of order N gives a rising slope of N*6 dB per decade). But wouldn't your example amount to 4.5 bits then? It's quite a lot either way.

 

[DonH56]

That's handy and makes sense (noise shaping of order N gives a rising slope of N*6 dB per decade). But wouldn't your example amount to 4.5 bits then? It's quite a lot either way.

The equation is actually (L+0.5) bits for each doubling of the sampling rate where L is the modulator order; SNR improves as (6L+3) dB for each doubling. I stated it in the DS article I linked, but should have restated it here to make that clear, sorry. When looking the other day I found my most current DS reference book was gone, with a sticky to remind me that I had loaned to a guy several years ago, and I have no idea where he or it is now. Multilevel, multistage topologies can get pretty complicated to analyze (and design) and may deviate from the simple equations. It gets deep fast...

It is also true that, without delta-sigma noise modulation (L = 0), you can gain 0.5 bit per doubling of sampling rate with a conventional DAC (or ADC) - assuming you maintain the same bandwidth and filter the out-of-band noise.