sphere shaped speakers

[flowolf]

Beautiful! Can you do any measurments?

How does it sound?

 

[rokr]

This is really cool, LOVE IT!!!
Congratulations @rokr !

I have ordered four CHN110 drivers, I am planning to do the same sometime next year
May I ask what you put under the speakers? That little wooden thingy

This is actually the smallest sister of the same blanda bowls line. I just cut the bottom.
It's not ready yet as i want smooth it and to add some silicone damping pads to the bottom and to where to speaker touches the stand.
Try to cut a bigger hole then in the image for better stability of the speaker.

 

[rokr]

Beautiful! Can you do any measurments?

I don't have any good measuring equipment. Will get some soon.
I'll try to run it through the Audyssey mic and app to maybe get some info.

 

[René - Acculution.com]

If I check Table I in the above PDF the first resonance they captured was at 963Hz - I guess it would be more interesting to see the resonances below 200Hz
But then if I check Fig. 1 it does show response from 0Hz and apparently there is only one resonance between 0 and 500Hz (around 400Hz)
Does this mean that (at least in the experiment mentioned in the PDF) there was no resonance below 400Hz?

Also it would be great if anybody here with experience in COMSOL could actually simulate the standing waves in a sphere.....

I have done this both analytically and numerically (COMSOL). Haven't read the thread, but if still relevant, I can perhaps put something together.

 

[ppataki]

I have done this both analytically and numerically (COMSOL). Haven't read the thread, but if still relevant, I can perhaps put something together.

Thank you @René - Acculution.com much appreciated, if you have the time
But I guess if the above idea is correct - like if let's say the inner diameter of a sphere is 26cm then the first standing wave will be at around 660Hz - then I am personally fine, no need for a simulation

 

[René - Acculution.com]

Thank you @René - Acculution.com much appreciated, if you have the time
But I guess if the above idea is correct - like if let's say the inner diameter of a sphere is 26cm then the first standing wave will be at around 660Hz - then I am personally fine, no need for a simulation

There is no mode at 660 Hz, but at 877 Hz there is. This modal approach has been tested up against this paper and fits (https://www.acs.psu.edu/drussell/Publications/Basketball.pdf). If you see a resonance at 660 Hz, there must be something more going on when the response is driven.

 

[rokr]

There is no mode at 660 Hz, but at 877 Hz there is. This modal approach has been tested up against this paper and fits (https://www.acs.psu.edu/drussell/Publications/Basketball.pdf). If you see a resonance at 660 Hz, there must be something more going on when the response is driven.
View attachment 334418

I don’t know how important it is for standing waves but the way I built it, it’s not a perfect sphere, the Y diameter is 28cm while the X diameter is 26cm( the internal dimensions are about 2 cm less in each direction).

 

[Flaesh]

Ancient Ellipsons. Back then they were made of plaster\gypsum, but I don’t know about today. Sealed, one FR driver.

 

[tktran303]

Spheroidal cabinets are excellent in terms of diffraction management.

Exhibit A:

raw response of a 6" midrange driver, in a 8" spheroidal cabinet, measured at 10 degrees intervals, at 1m. 5ms gate.
1/24 octave smoothing.

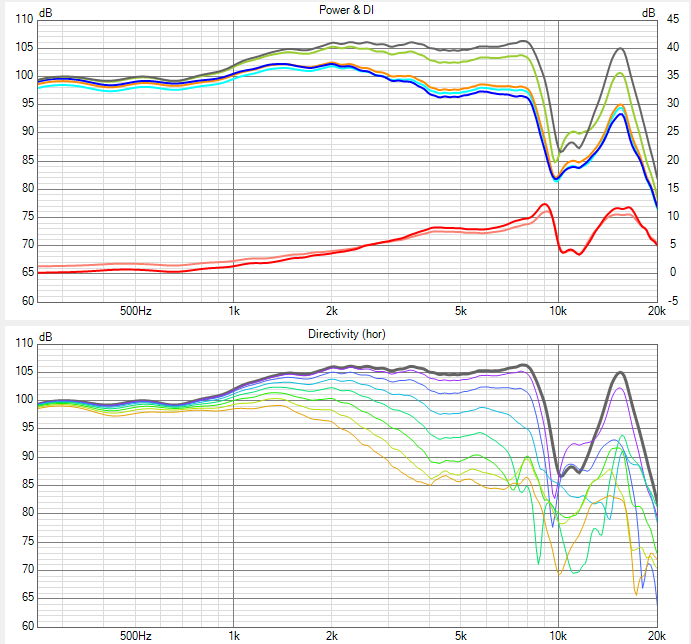
Tuning applied:

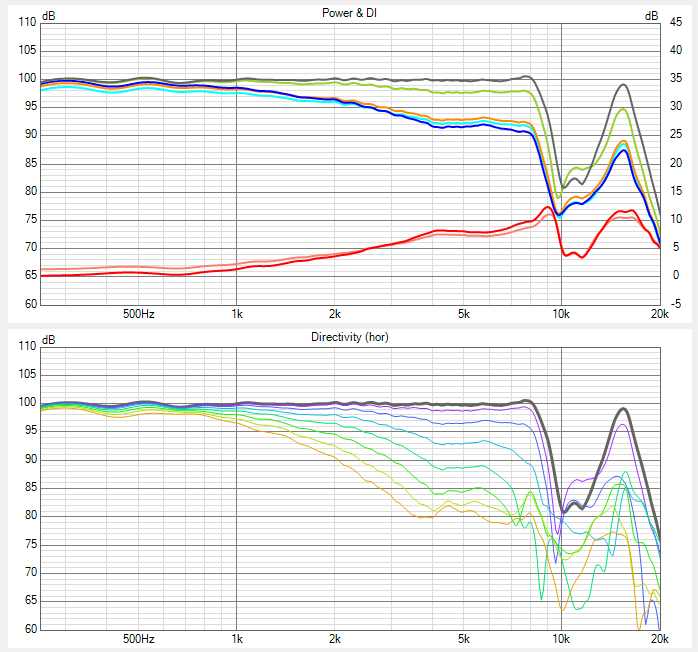
@René - Acculution.com

State of the art, don't you think?

 

[René - Acculution.com]

Spheroidal cabinets are excellent in terms of diffraction management.

Exhibit A:

raw response of a 6" midrange driver, in a 8" spheroidal cabinet, measured at 10 degrees intervals, at 1m. 5ms gate.
1/24 octave smoothing.

View attachment 334704


Tuning applied:

View attachment 334708


@René - Acculution.com

State of the art, don't you think?

Look good.

 

[ppataki]

This I believe is one more reason to go for this concept
My four CHN110 drivers arrived yesterday - I might only start the project in 6 months , but when I start I will definitely create a new thread where I will document it end-to-end with measurements

 

[highender]

Raw response, 4" midwoofer in a 22cm spherical cabinet.

 

[ernestcarl]

SE Electronics Munro Egg 150​

Excerpt from the review:

The physics of the situation is essentially that the sound wave generated by a loudspeaker driver radiates outwards in a hemispherical wave, travelling sideways across the baffle surface and out into the room. However, when the sound waves reach the baffle edge of a cuboid cabinet, they encounter a pressure discontinuity. There is nothing for the sound waves to press against any more, and that step change causes severe diffraction. In effect, the sharp cabinet edge forms a secondary source of sound-wave radiation, and sound waves from that 'virtual' source interfere with those from the loudspeaker driver itself, resulting in comb filtering, directional beaming and an uneven response. The precise frequencies affected and the strength of the interference effects depend on the relative distances between the driver and the various baffle edges.


Not surprisingly, Olson's work revealed that chamfering or rounding the front baffle edges helps to reduce these interference effects by softening the transition and severity of the pressure discontinuity at the cabinet edge — and that's why most modern loudspeaker cabinets have rounded edges to varying degrees. But the best performance was obtained with a spherical cabinet, since there are obviously absolutely no hard edges, and thus no step-change discontinuities.


However, a spherical cabinet presents other practical problems, not least being how to stop the speaker from rolling off the console meter-bridge! On a more serious note, a sphere has only one dimension and thus has a very strong resonant frequency. A better compromise, combining the soft baffle edges of a sphere but with a broad spread of internal resonant frequencies, is the ovoid or egg shape.

*The internal bracing ribs help to control cabinet resonances, while adding to the speaker's strength without significantly increasing its weight.

--------

Hmmmn... Don't know why more designers use an ovoid shape instead of a sphere.

 

[Flaesh]

https://en.elipson.com/product-page/bs50

 

[Killingbeans]

Cool, it seems to have the Helmholtz absorber, I was talking about in post #30.

Would love a spinorama, just to see the dispersion pattern. Probably pretty funky.

 

[Kal Rubinson]

https://en.elipson.com/product-page/bs50

I see these all the time locally but only in Forest Green:

 

[Flaesh]

I see these

I think it's different. Elipson has three wheels (see #68), but here there are four.

 

[Killingbeans]

The Elipson also doesn't have those anti-drag dimples that makes a turbulent boundary layer on the surface when going fast. Very important on a grill

 

[Flaesh]

doesn't have

Any owner of Elipson is free to cover it with dimples using a drilling machine or chisel and paint it ever Forest green.
BTW Elipson unique colours are Mercury ice, Saturn Dust and Neptune stone