- Joined
- May 1, 2021
- Messages
- 427
- Likes
- 1,309
As I see this being illustrated incorrectly very often, I will post here an example of how the phase delay and the group delay of a system affect the output of a system in each their own way.
What I see done most often is a reference/input signal is being 'shifted in phase' along a time axis, and then a delay (oftentimes denoted the group delay, because people think that is the 'proper' delay, in some sense) is associated with that resulting output signal; basically deducing the system from the signal. That is the wrong way around. For those steady-state signals, all you can see is the phase delay, which gives you no information about the group delay. If you DO know the phase and group delay of system, it means you know the phase of the system, and you can then (with also knowing the amplitude response), find the transfer function. When you have that, you can now find for example transient behavior, which will be affected by both phase delay and group delay of the system.
Knowing the phase delay at one singular frequency only, leaves you in the dark about the group delay, i.e. how is the phase changing and unwrapping 'around' that frequency; how is a GROUP of frequencies in the vicinity of this frequency each being affected by the phase changing and what does their envelope look like. The group delay could be zero, as for a polarity flip (that is another thing that people get wrong: Yes, a polarity flip is 180 degrees phase shift, AT ALL FREQUENCIES. Spread the word. That is how we assign a sign change to a transfer function, since magnitude has no sign). The phase delay, as well as the group delay, are both apparant delays. So looking at phase delay at a particular frequency, does not tell you that the apparent delay ACTUALLY came from the whole system being a pure delay, or that the group delay is equal to this observed delay: It tells you that for this frequency, you would NEED/GUESS AT this delay value for a pure delay system (linear phase at infinite bandwith -> phase delay=group delay=any latency), to have a STEADY-STATE output of the same phase and magnitude. But you do not KNOW at all that your system and that delay system are the same, even at that one frequency, and typically they are of course not the same at any frequency, and so they will have different transient behavior (but the same steady-state at this particular frequency, and perhaps at other frequencies).
The next part is repeated from another blog post on this site:
_________________________________________________________________________
So, here is the issue with using these steady-state signals:
Group delay is correctly defined so far; -d(phase(omega))/d(omega)
Phase delay is correctly defined as -phase(omega)/omega.
Here, omega is the angular frequency; 2 times pi times frequency.
We now define a 2nd order allpass filter via the transfer function H(s)=(s^2-omega0*s/Q+omega^2)/ (s^2+omega0*s/Q+omega^2).
We set the Q to some value; here 0.707. And the characteristic angular frequency to 1,000 rad/s, which is 159 Hz in frequency terms.
We plot the phase, here in wrapped version, as a function of frequency:
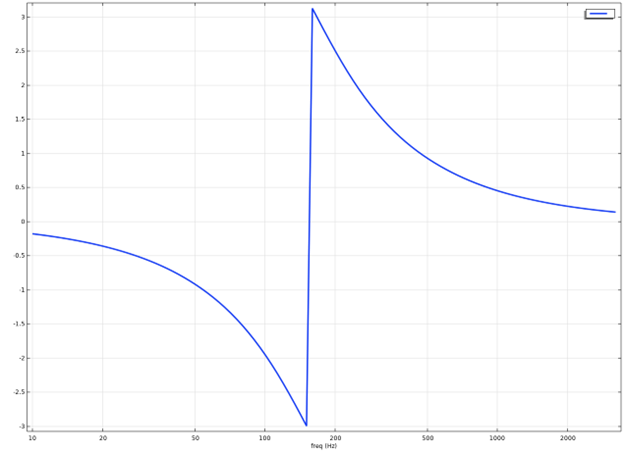
We calculate the phase delay and group delay associated with the system, taking care to note that the derivatives are defined via angular frequencies not frequency, and taking unwrapping of the phase into account to avoid discontinuities that would be unphysical.
We plot them as function of frequency, including their differential:
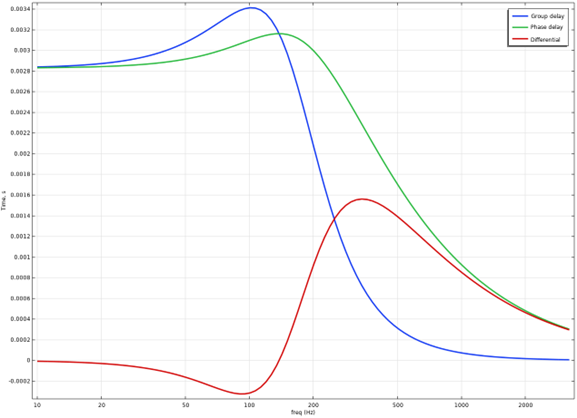
We zoom in on the frequency 159 Hz as an example:
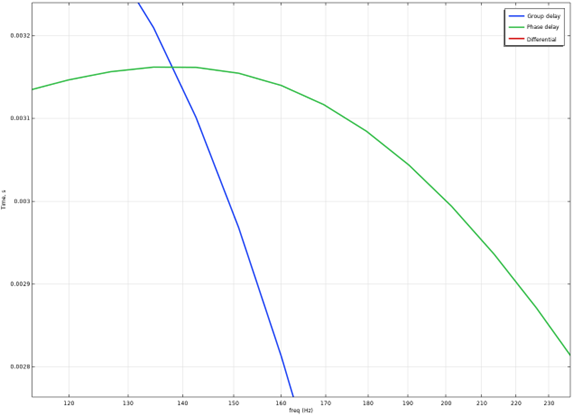
We note that at this frequency the phase delay is around 0.0313-ish s and the group delay is 0.028-ish s.
We now calculate the full response of this system, including transient behavior(!), for an input sinusoidal signal with a frequency of 159 Hz, and plot from t=t0=0 s.
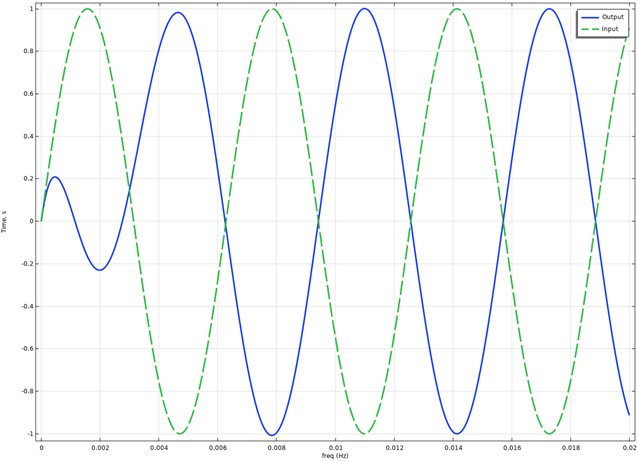
We now zoom in at the response as it has reached steady-state conditions.
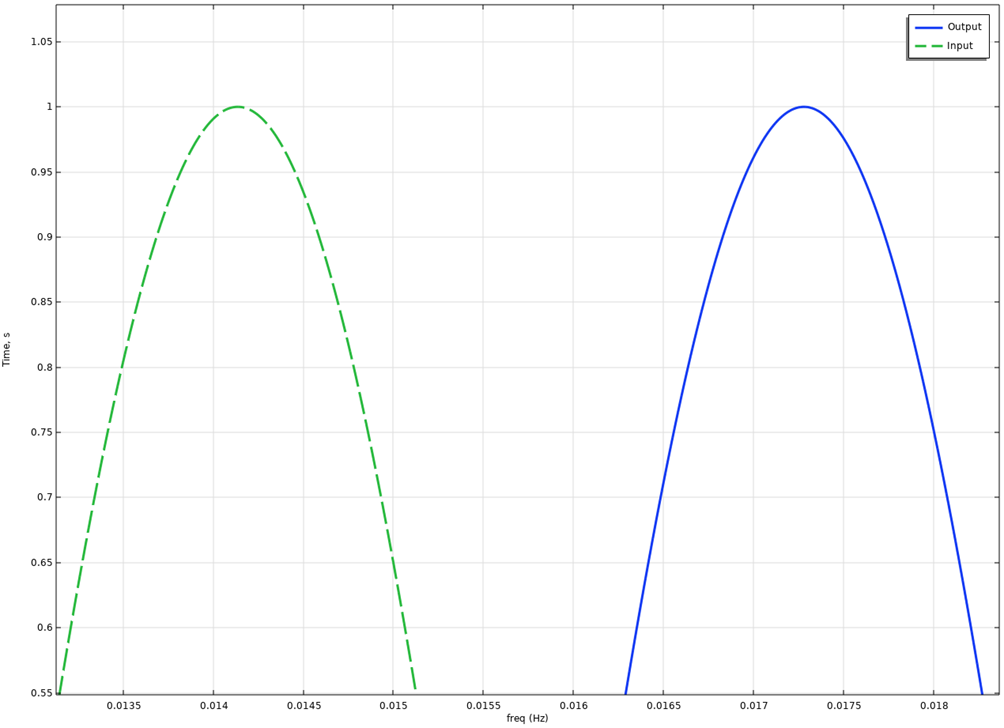
We note the “apparent delay”, when looking at the delta between a peak in input vs peak in output is 0.0313-ish seconds; the PHASE DELAY.
Ergo: Looking at how these discrete frequency signals are “shifted in phase/time” under steady-state conditions tells us absolutely nothing about the topic; group delay. It gives us their associated phase delay. There are infinitely many systems that could give us this steady-state output for this given frequency; showing the steady-state output does not give us any information about the group delay, as any slope of the phase will not be seen, only the phase value itself (you cannot calculate the derivative in a point without knowledge about adjacent points). (Of course, with this phase delay information for enough frequencies, we could derive a smooth phase via interpolation, and calculate the group delay from there.)
An example of one such system giving us the same steady-state at this frequency is a polarity flip; a 180 degrees phase shift; which is a transfer function of H(s)=-1. Note how when steady-state conditions are reached for our allpass system, the output looks exactly like a flipped version of the input, because the phase is, for both systems, 180 degrees at this particular frequency. What is different, however, is their transient behavior, as we can clearly see from my more elaborate calculation using Inverse Laplace transformation: Our original allpass filter takes time to settle, while a polarity flip-system would immediately output an inverted version of the input. Same steady-state. Same phase delay. Different group delay. At this particular frequency.
So, even looking at a multitude of frequencies, for example the Fourier components of a square signal, each of these will be shifted by their phase delay, as all of the above has to hold for any frequency (the phase will of course not be that of a polarity flip at all of them, but that was just to make a strong point for the chosen frequency). We do not have any ‘group’ of frequencies around one particular frequency, and we cannot deduce transient behavior of the system. All we know from those plots are the phase values for each frequency, but any phase line drawn that goes through these discrete frequency points will satisfy the shown steady-state outputs, and we don’t know the slope (group delay), even if there of course is one associated with the process that created the signals in the first place.
So, the title of post should be ‘phase delay’, not ‘group delay’
Edit: A final note should be that at no frequency will the allpass system acts a pure latency/transport delay. As we go to lower and lower frequencies, the differential between phase delay and group delay will tend to 0, but never reach it. So a very low frequency sinusoidal input will look as if its transient output is first a delay, and then the output will be a phase shifted version of the input, but zoom in enough at that first part, and you will see it slightly deviate from a pure zero. At 159 Hz there is a significant differential delay, and so the transient output has a much more clear non-zero immediate output.
What I see done most often is a reference/input signal is being 'shifted in phase' along a time axis, and then a delay (oftentimes denoted the group delay, because people think that is the 'proper' delay, in some sense) is associated with that resulting output signal; basically deducing the system from the signal. That is the wrong way around. For those steady-state signals, all you can see is the phase delay, which gives you no information about the group delay. If you DO know the phase and group delay of system, it means you know the phase of the system, and you can then (with also knowing the amplitude response), find the transfer function. When you have that, you can now find for example transient behavior, which will be affected by both phase delay and group delay of the system.
Knowing the phase delay at one singular frequency only, leaves you in the dark about the group delay, i.e. how is the phase changing and unwrapping 'around' that frequency; how is a GROUP of frequencies in the vicinity of this frequency each being affected by the phase changing and what does their envelope look like. The group delay could be zero, as for a polarity flip (that is another thing that people get wrong: Yes, a polarity flip is 180 degrees phase shift, AT ALL FREQUENCIES. Spread the word. That is how we assign a sign change to a transfer function, since magnitude has no sign). The phase delay, as well as the group delay, are both apparant delays. So looking at phase delay at a particular frequency, does not tell you that the apparent delay ACTUALLY came from the whole system being a pure delay, or that the group delay is equal to this observed delay: It tells you that for this frequency, you would NEED/GUESS AT this delay value for a pure delay system (linear phase at infinite bandwith -> phase delay=group delay=any latency), to have a STEADY-STATE output of the same phase and magnitude. But you do not KNOW at all that your system and that delay system are the same, even at that one frequency, and typically they are of course not the same at any frequency, and so they will have different transient behavior (but the same steady-state at this particular frequency, and perhaps at other frequencies).
The next part is repeated from another blog post on this site:
_________________________________________________________________________
So, here is the issue with using these steady-state signals:
Group delay is correctly defined so far; -d(phase(omega))/d(omega)
Phase delay is correctly defined as -phase(omega)/omega.
Here, omega is the angular frequency; 2 times pi times frequency.
We now define a 2nd order allpass filter via the transfer function H(s)=(s^2-omega0*s/Q+omega^2)/ (s^2+omega0*s/Q+omega^2).
We set the Q to some value; here 0.707. And the characteristic angular frequency to 1,000 rad/s, which is 159 Hz in frequency terms.
We plot the phase, here in wrapped version, as a function of frequency:
We calculate the phase delay and group delay associated with the system, taking care to note that the derivatives are defined via angular frequencies not frequency, and taking unwrapping of the phase into account to avoid discontinuities that would be unphysical.
We plot them as function of frequency, including their differential:
We zoom in on the frequency 159 Hz as an example:
We note that at this frequency the phase delay is around 0.0313-ish s and the group delay is 0.028-ish s.
We now calculate the full response of this system, including transient behavior(!), for an input sinusoidal signal with a frequency of 159 Hz, and plot from t=t0=0 s.
We now zoom in at the response as it has reached steady-state conditions.
We note the “apparent delay”, when looking at the delta between a peak in input vs peak in output is 0.0313-ish seconds; the PHASE DELAY.
Ergo: Looking at how these discrete frequency signals are “shifted in phase/time” under steady-state conditions tells us absolutely nothing about the topic; group delay. It gives us their associated phase delay. There are infinitely many systems that could give us this steady-state output for this given frequency; showing the steady-state output does not give us any information about the group delay, as any slope of the phase will not be seen, only the phase value itself (you cannot calculate the derivative in a point without knowledge about adjacent points). (Of course, with this phase delay information for enough frequencies, we could derive a smooth phase via interpolation, and calculate the group delay from there.)
An example of one such system giving us the same steady-state at this frequency is a polarity flip; a 180 degrees phase shift; which is a transfer function of H(s)=-1. Note how when steady-state conditions are reached for our allpass system, the output looks exactly like a flipped version of the input, because the phase is, for both systems, 180 degrees at this particular frequency. What is different, however, is their transient behavior, as we can clearly see from my more elaborate calculation using Inverse Laplace transformation: Our original allpass filter takes time to settle, while a polarity flip-system would immediately output an inverted version of the input. Same steady-state. Same phase delay. Different group delay. At this particular frequency.
So, even looking at a multitude of frequencies, for example the Fourier components of a square signal, each of these will be shifted by their phase delay, as all of the above has to hold for any frequency (the phase will of course not be that of a polarity flip at all of them, but that was just to make a strong point for the chosen frequency). We do not have any ‘group’ of frequencies around one particular frequency, and we cannot deduce transient behavior of the system. All we know from those plots are the phase values for each frequency, but any phase line drawn that goes through these discrete frequency points will satisfy the shown steady-state outputs, and we don’t know the slope (group delay), even if there of course is one associated with the process that created the signals in the first place.
So, the title of post should be ‘phase delay’, not ‘group delay’
Edit: A final note should be that at no frequency will the allpass system acts a pure latency/transport delay. As we go to lower and lower frequencies, the differential between phase delay and group delay will tend to 0, but never reach it. So a very low frequency sinusoidal input will look as if its transient output is first a delay, and then the output will be a phase shifted version of the input, but zoom in enough at that first part, and you will see it slightly deviate from a pure zero. At 159 Hz there is a significant differential delay, and so the transient output has a much more clear non-zero immediate output.
Last edited:
