In-room quasi-anechoic measurement using beamforming MMM

[Keith_W]

Dear mods: I looked for another thread describing Krol's method but I was surprised that I could not find one. If there is an existing thread, would you be kind enough to merge it?

Krol et al published a paper in 2013 describing this method. This paper is available for download from ASR here.

Krol notes that Maximum Length Sequence measurements (commonly known as logarithmic sweeps) have a lower frequency limit imposed by reflecting boundaries. He proposed an alternative method via delay-sum beamforming. Essentially, the microphone is shifted in a straight line towards the loudspeaker and the measurement is repeated multiple times. The idea is that the direct sound from the speaker remains correlated, but the reflections are not. If the responses are summed, the influence of reflections is reduced.

As the microphone gets closer to the speaker, the time of flight delay will be reduced. The measurements will need to be adjusted for delays. The delay can be calculated with t = d/c where t is time in seconds (multiply by 1000 for milliseconds), d is the distance between microphone and speaker in meters or feet, and c is the speed of sound (343m/s, or 1125 ft/s). Rotate each measurement by the calculated delay.

Krol's paper includes a comparison between his described method and the anechoic response, shown above.

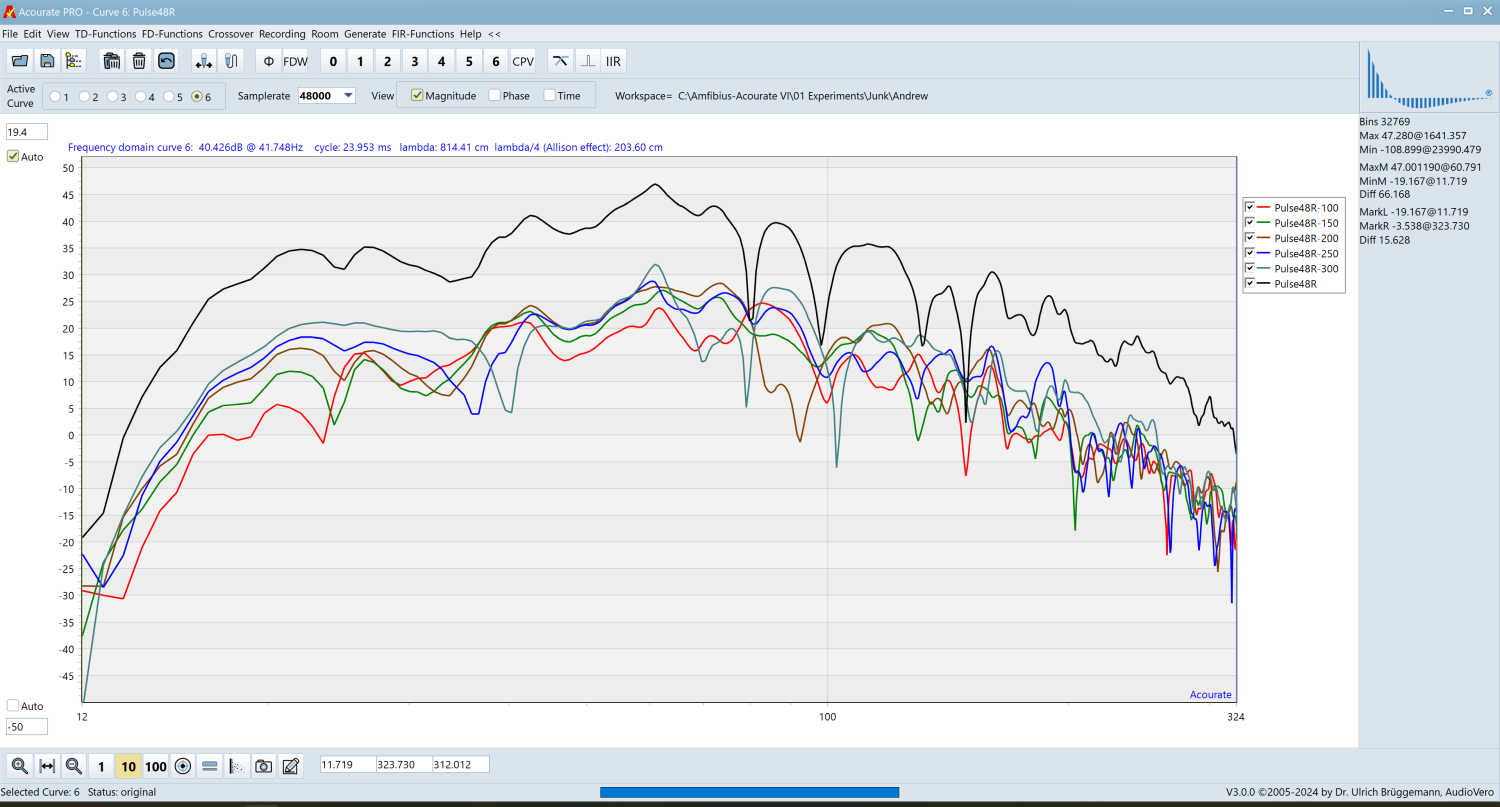
I tried this method at home. A tape measure was placed on the floor on the axis of the speaker. I wanted to avoid capturing the nearfield response, so I stopped measuring 1m from the speaker. Sweeps were taken at 25cm intervals. I then adjusted the delay of all measurements and summed them. I should theoretically adjust the gain, but I did not do so. The above illustration shows the sum (black curve) of multiple measurements (all the curves below) taken 25cm apart. Only the woofer was swept.

I thought that it would be even faster to perform an MMM instead of multiple logarithmic sweeps. The disadvantage of the MMM is that it captures the amplitude response only with no phase or timing information. This was not described by Krol in his paper. To my knowledge, there is no published documentation of this method comparing it to an anechoic response. So be warned - the method I am about to describe is unpublished and not peer reviewed. I am submitting this method to ASR for "peer review" so please be as savage as you like.

I started my software's MMM recorder and swept along a straight line on axis to the speaker.

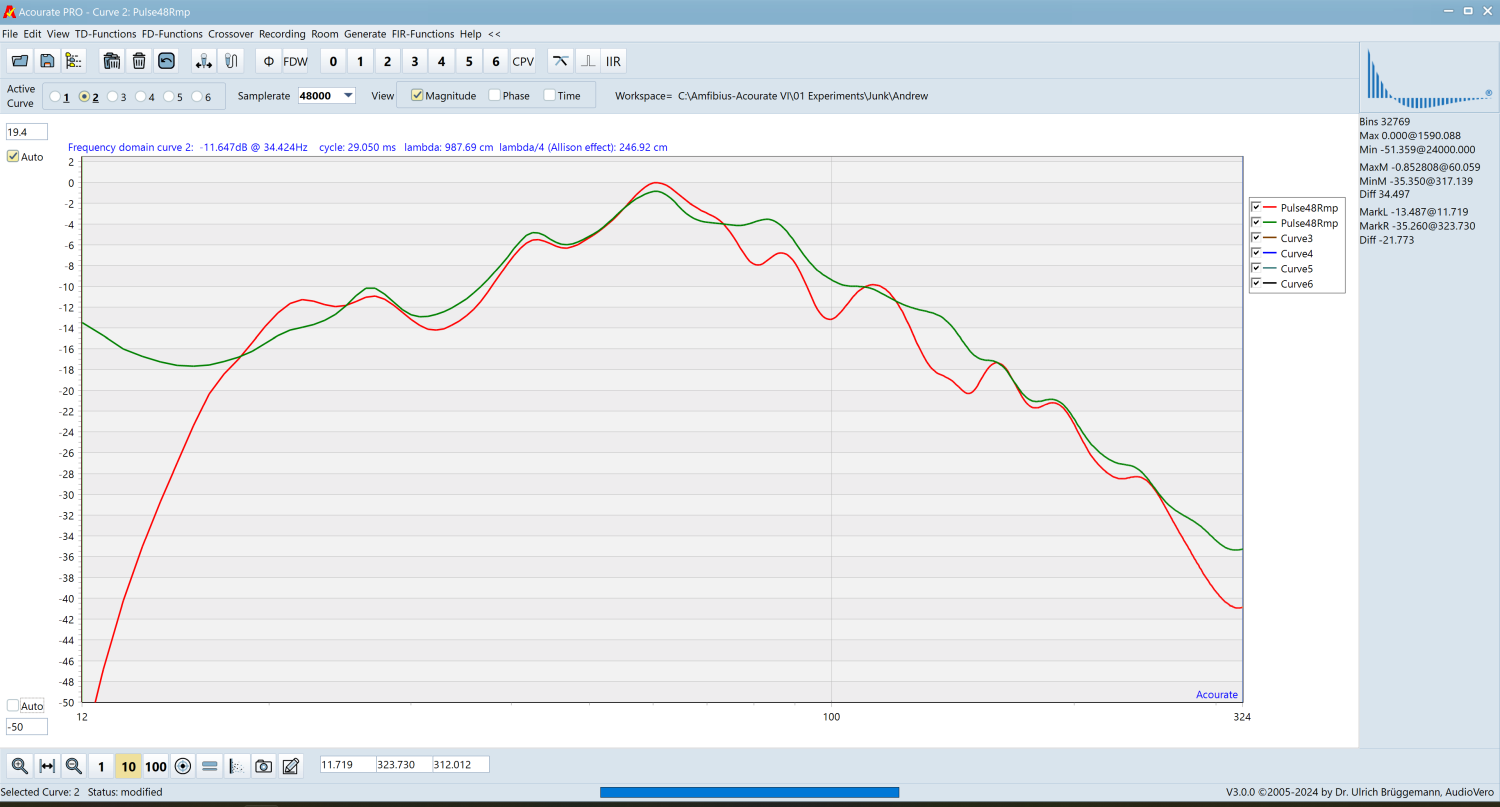
The above shows a comparison between Krol’s delay-sum method (red) and my proposed method using an MMM (green). There is acceptable correlation between the two methods. The rising bass response <20Hz is probably due to an artefact from microphone movement. I do not have an anechoic measurement for comparison.

My logic: if Krol's method compares favourably with the anechoic response, and the MMM method compares favourably with Krol's, then it should be a good approximation of the anechoic response.

Comments and criticism appreciated.

 

[3ll3d00d]

It's a woofer being measured? The ripples and variations + large differences looks pretty much nothing like anechoic to me for a woofer.

 

[LionIT]

Interesting thread.
I seems to understand the beamforming principle is based on the fact that the level of indirect sound is lower than direct one and especially it varies in delay changing mic position, so by adding n times the IR of different positions the direct sound prevails (so the anechoic response). So I suppose more measurements lead to a more accurate result.
The MMM technique, on the other hand, seems to me to make an average of FR rather than a sum of IR, so the similarity to the anechoic response is more dependent on room reflection.
In your comparison I suppose you need way more sample with the beamforming technique to have a valid result, otherwise you risk comparing the same reflections in some case.
Note: obviously the sum of all samples will have to be divided by the number of samples in the end.

 

[RandomEar]

Interesting thread.
I seems to understand the beamforming principle is based on the fact that the level of indirect sound is lower than direct one and varies with mic position, so by adding n times the IR of different positions the direct sound prevails (so the anechoic response). So I suppose more measurements lead to a more accurate result.
The MMM technique, on the other hand, seems to me to make an average rather than a sum, so the similarity to the anechoic response is more dependent on room reflection.
In your comparison I suppose you need way more sample with the beamforming technique to have a valid result, otherwise you risk comparing the same reflections in some case.
Note: obviously the sum of all samples will have to be divided by the number of samples in the end.

@LionIT I'm pretty sure it's the same thing. The MMM technique should yield the exact same result as the summed (actually averaged, because otherwise you'd approach insane summed SPLs) individual stationary measurements for n stationary measurements with n->infinity.

In pratice, the methods won't deliver exactly the same results, as MMM tends to inject handling noise into the measurement and you tend to have less total measurement time with MMM if you only use one sweep. That decreases the SNR. I would also assume that you will be more likely to see artifacts of room modes in MMM results, as you might accidentally move through one interference node at the exact point in time the sweep hits that node's frequency. It's not super likely, but it can happen.

@Keith_W Very interesting idea! Maybe you could further improve it by making two MMM passes: One moving towards the speaker and one moving away from it. These could then be averaged. I assume this would further reduce the influence of "accidentally" captured reflections in a single pass and would also eliminate the doppler shift you technically baked into the MMM by moving towards the speaker (although it's probably irrelevant anyway, considering the magnitude of other sources of error).

 

[LionIT]

@LionIT I'm pretty sure it's the same thing. The MMM technique should yield the exact same result as the summed (actually averaged, because otherwise you'd approach insane summed SPLs) individual stationary measurements for n stationary measurements with n->infinity.

In pratice, the methods won't deliver exactly the same results, as MMM tends to inject handling noise into the measurement and you tend to have less total measurement time with MMM if you only use one sweep. That decreases the SNR. I would also assume that you will be more likely to see artifacts of room modes in MMM results, as you might accidentally move through one interference node at the exact point in time the sweep hits that node's frequency. It's not super likely, but it can happen.

@Keith_W Very interesting idea! Maybe you could further improve it by making two MMM passes: One moving towards the speaker and one moving away from it. These could then be averaged. I assume this would further reduce the influence of "accidentally" captured reflections in a single pass and would also eliminate the doppler shift you technically baked into the MMM by moving towards the speaker (although it's probably irrelevant anyway, considering the magnitude of other sources of error).

As far as I understand it is not the same because MMM does not sum time aligned IR. It does the simple average of the frequency response. Therefore indirect sound is added up each time like direct sound. While with beamforming the indirect sound occurs at several delays from the direct one and therefore the sum is uncorrelated. For this reason it improves the ratio between direct and indirect sound, proportionally to the number of samples.
I also believe that the microphone translation scheme is relevant in reducing the correlation between direct and indirect sounds, but I can't find any info about it.

But maybe I'm wrong about IR alignment and sum with MMM?
In fact, I don't think there is a definition ... it is more a question of method perhaps.

PS. Does anyone know how the Direct Sound Separation Module of the Klippel NFS works?
I believe that knowing the exact position of the microphone (being robotic) can make differential calculations to effectively isolate the direct sound, without working proportionally on the ratio between it and indirect sound.

 

[RandomEar]

As far as I understand it is not the same because MMM does not sum time aligned IR. It does the simple average of the frequency response. Therefore indirect sound is added up each time like direct sound. While with beamforming the indirect sound occurs at several delays from the direct one and therefore the sum is uncorrelated. For this reason it improves the ratio between direct and indirect sound, proportionally to the number of samples.
I also believe that the microphone translation scheme is relevant in reducing the correlation between direct and indirect sounds, but I can't find any info about it.

But maybe I'm wrong about IR alignment and sum with MMM?
In fact, I don't think there is a definition ... it is more a question of method perhaps.

I'm not 100% sure either, especially about the impact of reflections/indirect sound. But to reiterate the point: If you take a sum and divide by the number of samples or points (which is what's happening as far as I understand), you get the average. There's nothing to differentiate, there. You're right, though, that the SNR (and direct sound to reflection ratio) of individual stationary measurements will be higher.

If the direct and indirect sound are correlated when using MMM should depend on how you set up the sweep, I think: If you sweep only once and finish all movements during that sweep, there will be correlation. But it will likely be low and non-reproducible, unless you move the microphone in a highly reproducible way using rails and a motor or something. If a person moves the microphone, no two MMM's will be identical and any correlation will depend on how fast and consistent you move and when exactly the sweep reaches the mic during your movement. That's pretty random. So you could potentially mitigate most of those reflection artifacts by simply running the MMM twice, as suggested above. Still faster than running ten or so stationary measurements for the beamforming method.

If you allow for multiple full sweeps during your movements towards the speaker, results should be almost identical to the beamforming/stationary method, even with only doing one MMM run, I think. Apart from the handling noise and stuff.

 

[Blumlein 88]

Have you tried a spiral pattern moving toward the speaker? This should reduce room modes. Or maybe that is what you are already doing.

 

[LionIT]

I'm not 100% sure either, especially about the impact of reflections/indirect sound. But to reiterate the point: If you take a sum and divide by the number of samples or points (which is what's happening as far as I understand), you get the average. There's nothing to differentiate, there. You're right, though, that the SNR (and direct sound to reflection ratio) of individual stationary measurements will be higher.

If the direct and indirect sound are correlated when using MMM should depend on how you set up the sweep, I think: If you sweep only once and finish all movements during that sweep, there will be correlation. But it will likely be low and non-reproducible, unless you move the microphone in a highly reproducible way using rails and a motor or something. If a person moves the microphone, no two MMM's will be identical and any correlation will depend on how fast and consistent you move and when exactly the sweep reaches the mic during your movement. That's pretty random. So you could potentially mitigate most of those reflection artifacts by simply running the MMM twice, as suggested above. Still faster than running ten or so stationary measurements for the beamforming method.

If you allow for multiple full sweeps during your movements towards the speaker, results should be almost identical to the beamforming/stationary method, even with only doing one MMM run, I think. Apart from the handling noise and stuff.

The point is how the average happens with MMM.
If it is the FR that is averaged (intended as the average of the FFTs) then the ratio between direct and indirect sound does not change (or change in a way dependent on the room vs mic pos).
If instead the IRs are averaged, previously temporally aligned with each other on the main peak, then the rate improves proportionally to the number of samples, because when moving the microphone the reflections in the IR occur at different delays from the peak of the direct sound, therefore they do not add together (exactly what is illustrated in the Krol paper as a beamforming technique).
It is not clear, or simply not defined, whether the MMM technique involves one thing or the other...

 

[LionIT]

I found a very explanatory document on MMM which clearly states the following:

MMM is quick and and efficient for equalization of a loudspeakers but because it is missing the time and phase information, it is not a tool to set up crossovers, time align speakers,...

I believe this confirms the fact that MMM and beamforming are not interchangeable but intended for different purposes.
Beamforming is therefore theoretically more suitable for detecting the quasi-anechoic response (where done correctly).

 

[Blumlein 88]

I found a very explanatory document on MMM which clearly states the following:

I believe this confirms the fact that MMM and beamforming are not interchangeable but intended for different purposes.
Beamforming is therefore theoretically more suitable for detecting the quasi-anechoic response (where done correctly).

I am not sure your conclusion automatically follows from the difference in the two methods.

 

[LionIT]

I am not sure your conclusion automatically follows from the difference in the two methods.

In the same document, this is stated:

a3 Comparison between Harman's results and P360 in a living room :
above 150-200Hz, MMM curve is between « direct sound » and « first reflections »

Reasonably what is expected from the method, and reason why it is suitable for representing perception in the room.
In fact it should be similar (or conceptually similar) to the CEA2034 Estimated in Room Response (12% Listening Window, 44% Early Reflections, 44% Sound Power).

Beamforming, on the other hand, seems to have been conceived to refer more faithfully to the anechoic response (for the necessary purposes).

This is why it made sense to me to consider the two methods to be non-alternative.

 

[Blumlein 88]

One method is averaging multiple positions so direct sound counts for more than reflections. The other inherently is averaging multiple positions over time. Which might achieve something similar in FR though not phase. My picture of the op description is moving linearly toward the speaker.

 

[LionIT]

Linear movement with MMM seems really not optimal.
Optimal seems to be helix of 10m length.

As a reference, ISO/FDIS 16283-1:2013 recommends 5 measurements which gives a scanning length of 10m and validity down to about 100Hz (see Neq=5 line in picture 12).

I can't find any movement information about beamforming though.
In any case, different acoustic information seem to provided by each method.

 

[Blumlein 88]

Linear movement with MMM seems really not optimal.
Optimal seems to be helix of 10m length.

I can't find any movement information about beamforming though.
In any case, different information seem to provided by each method.

I do believe the illustration and recommendations are for pink noise in large venues. There have been enough people using smaller movements in home listening rooms to show the result is pretty much the same as several sweeps averaged around the listener. I measured both ways and showed virtually identical response in some thread or another around hear. Others have done the same. It makes sense for the use cases involved. In a venue or theater you want a larger area considered, while in your listening room the space you are concerned with is much smaller.