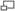A DC voltage across a cap produces zero magnetic field. And the electric field stays almost entirely in the cap.
On the contrary, stray magnetic fields are always part of real world models of capacitors. Because it has to do with the construction.
An example:
Magnetic Field from a Charging Capacitor
Suppose you have a parallel plate capacitor that is charging with a current I=3 A
. The plates are circular, with radius R=10 m and a distance d=1 cm
apart. What is the magnetic field in the plane parallel to but in between the plates?
Charging Capacitors
Facts
- The capacitor is a parallel plate capacitor with circular plates.
- R=10 m
- d=1 cm
- The capacitor is charging with a current I=3 A
Lacking
- A description of the magnetic field.
Approximations & Assumptions
- We are only concerned about a snapshot in time, so the current is I
- , even though this may change at a later time as the capacitor charges.
- The electric field between the plates is the same as the electric field between infinite plates (we'll ignore the electric field at the edges of the capacitor): This allows us to assume the electric field is constant between the plates. This is a good assumption with two big plates that are very close together.
- The electric field outside the plates is zero: This also ties back to having two big plates separated by a small distance. Making this assumption allows us to simplify down our equations when calculating the flux through our surface.
Representations
- We represent the electric field in a parallel plate capacitor as
E⃗ =Q/Aϵ0x^
where Q is the charge on a plate, A is the area of the plate, and x^
- is directed from one plate to the other.
- We can represent the magnetic field from a changing electric field as
∫B⃗ ∙dl⃗ =μ0Ienc+μ0ϵ0dΦEdt
- We represent the situation with the following visual:

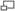
Plane in which we wish to find B-field
Solution
We wish to find the magnetic field in the plane we've shown in the representations. We know from the notes that a changing electric field should create a curly magnetic field. Since the capacitor plates are charging, the electric field between the two plates will be increasing and thus create a curly magnetic field. We will think about two cases: one that looks at the magnetic field inside the capacitor and one that looks at the magnetic field outside the capacitor.
Due to the circular symmetry of the problem, we choose a circular loop in which to situate our integral ∫B⃗ ∙dl⃗
. We also choose for the loop to be the perimeter of a flat surface, so that the entire thing lies in the plane of interest, and there is no enclosed current (so Ienc=0
- there is only the changing electric field). We show the drawn loop below, split into two cases on the radius of the loop.
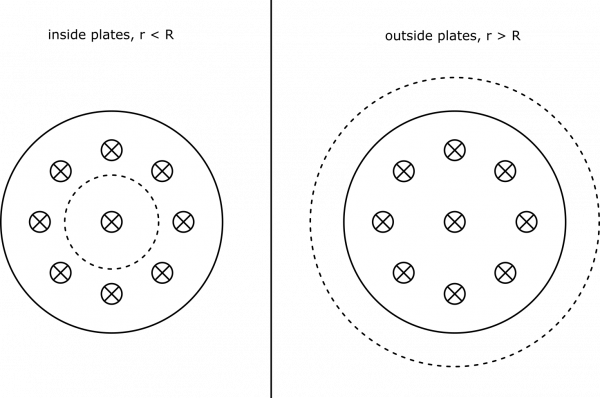
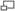
Circular Loops
Below, we also draw the direction of the magnetic field along the loops. We know the magnetic field is directed along our circular loop (since the changing electric flux creates a curly magnetic field) – if it pointed in or out a little bit, we may be able to conceive of the closed surface with magnetic flux through it, which would imply the existence of a magnetic monopole. This cannot be the case! We also know that the field is directed counterclockwise, due to the increasing electric field into the page. (This comes from an extension of Lenz's Law, but will not needed for this course).
Circular Loops, with B-field shown
We are pretty well set up to simplify our calculation of the integral in the representations, since the B-field is parallel to the loop's perimeter. Below, we show the integral calculation, where the magnetic field at a radius r
is displayed as B(r)
.
∫B⃗ ∙dl⃗ =∫B(r)dl=B(r)∫dl=2πrB(r)
Next, we need to find the changing electric flux in our loop. Since our loop was described with a flat surface, and the electric field is directed parallel to the area-vector of the loop, we can write electric flux as ΦE=E⃗ ∙A⃗ =EA
. This formula will need to be split up for parts of the surface inside the plates versus outside, since the electric field is different.
ΦE, in=EA=Q/Aplateϵ0Aloop=Qϵ0πR2πr2=Qr2ϵ0R2
ΦE, out=EA=EinAin+EoutAout=Q/Aplateϵ0Aplate+0=Qϵ0πR2πR2=Qϵ0
Now, if we wish the find the change in flux, we will take a time derivative. Notice that all the terms in the flux expressions above are constant, except for Q
, which is changing with time as dictated by I
.
dΦEdt=dQdtr2ϵ0R2=Ir2ϵ0R2, inside, r<R
dΦEdt=dQdtϵ0=Iϵ0, outside, r>R
We can now connect the pieces together (remember, Ienc=0
, so we omit it below). We can write:
2πrB(r)=∫B⃗ ∙dl⃗ =μ0ϵ0dΦEdt=μ0Ir2R2, inside, r<R
2πrB(r)=∫B⃗ ∙dl⃗ =μ0ϵ0dΦEdt=μ0I, outside, r>R
We are ready to write out the magnetic field.
B(r)=⎧⎩⎨μ0Ir2πR2μ0I2πrr<Rr>R
Notice, the distance between the plates has no effect on the magnetic field calculation. Also, the amount of the charge on the plates at a given time does not matter – we only care about how fast the charge is changing (the current!). Also, it is interesting that outside the plates, the magnetic field is the same as it would be for a long wire. This would be just as if the capacitor were not there, and the wire were connected. Below, we show a graph of the magnetic field strength as a function of the distance from the center of the capacitor.
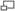
B-Field Strength, Graphed
We have enough information to find the maximum B-field, which is at the edge of the plates:
Bmax=μ0I2πR=4π⋅10−7Tm/A⋅3 A2π⋅10 m=60 nT
Of course we can look at a research paper about a particular type as well:
https://www.researchgate.net/figure...citors-fabricated-from-polymer_fig4_224750062