- Joined
- May 1, 2021
- Messages
- 431
- Likes
- 1,328
I will give a short introduction via simulations in COMSOL Multiphysics to the ‘Double Array Bass’ subwoofer setup and how the response will differ between an idealized situation of two walls moving compared to having a finite number of subwoofers.
Imagine first a 3x4x5 meters room. We can calculate the associated room modes as shown below.
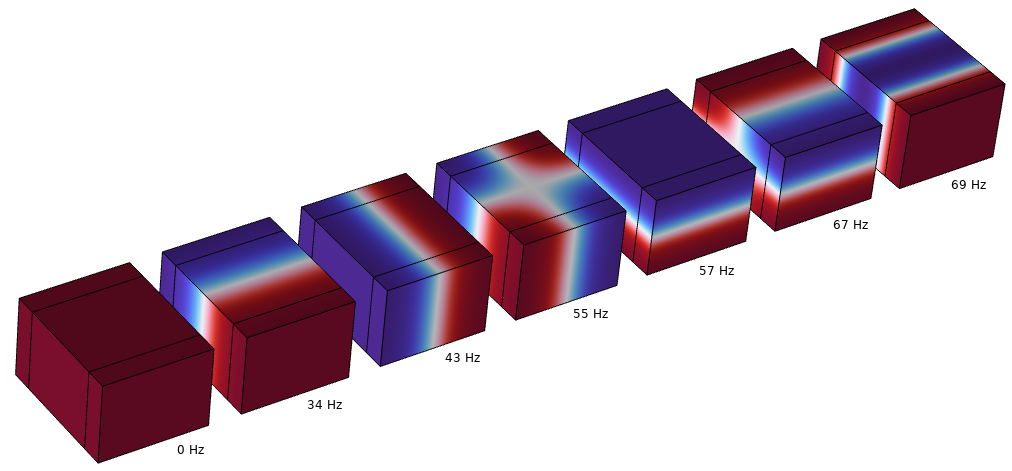
These modes are an inherent feature of the room geometry and air being the medium inside it. They exist independent of any sources and are calculated without any regard to sourcing. Whether a mode is a problem or not will be evaluated when a source(s) is activated. Let us now put a subwoofer in the corner and evaluate the sound pressure level in 6 preselected places at a height of 1.1 meters.
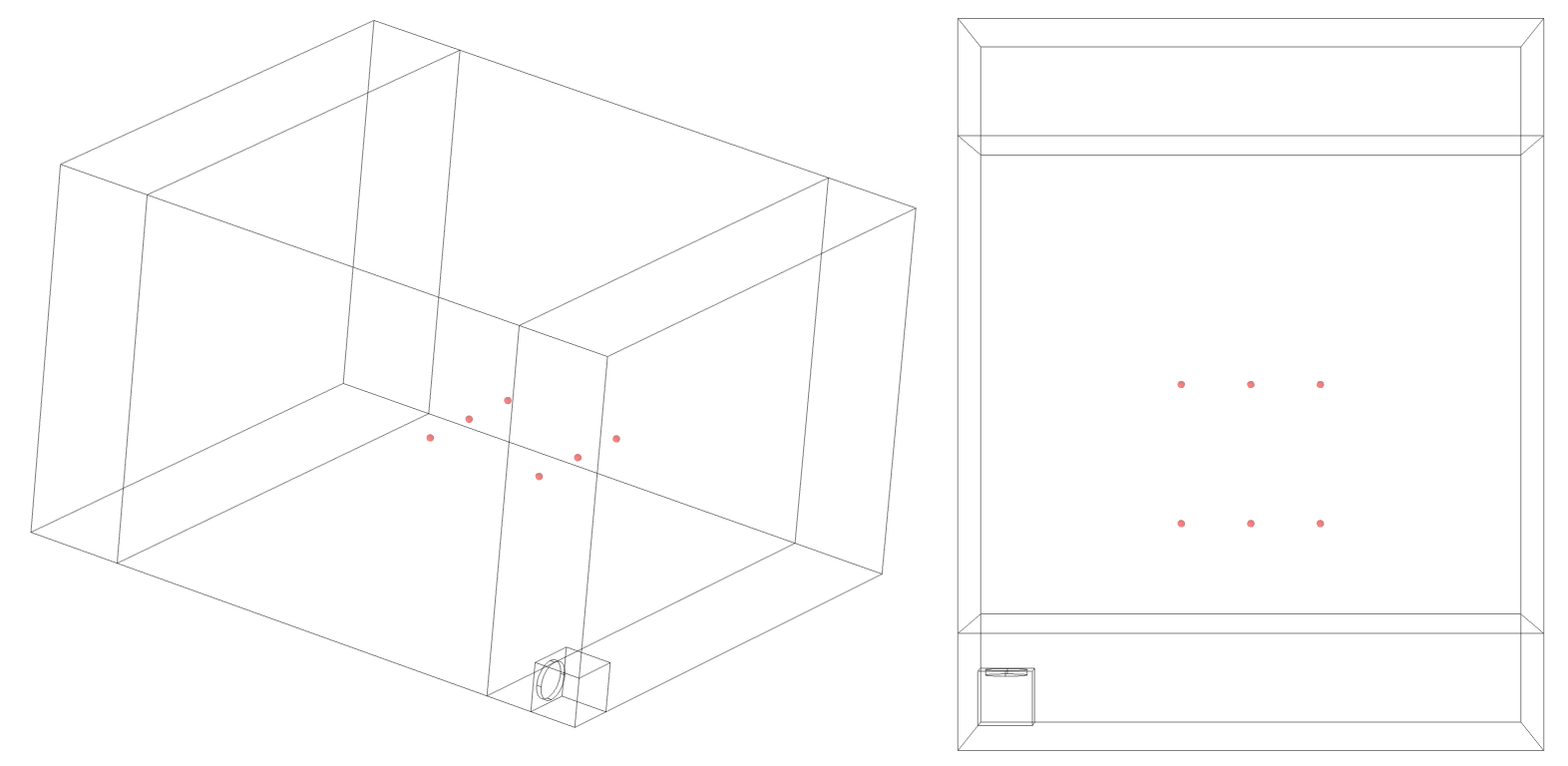
The responses in the points vary quite a bit.
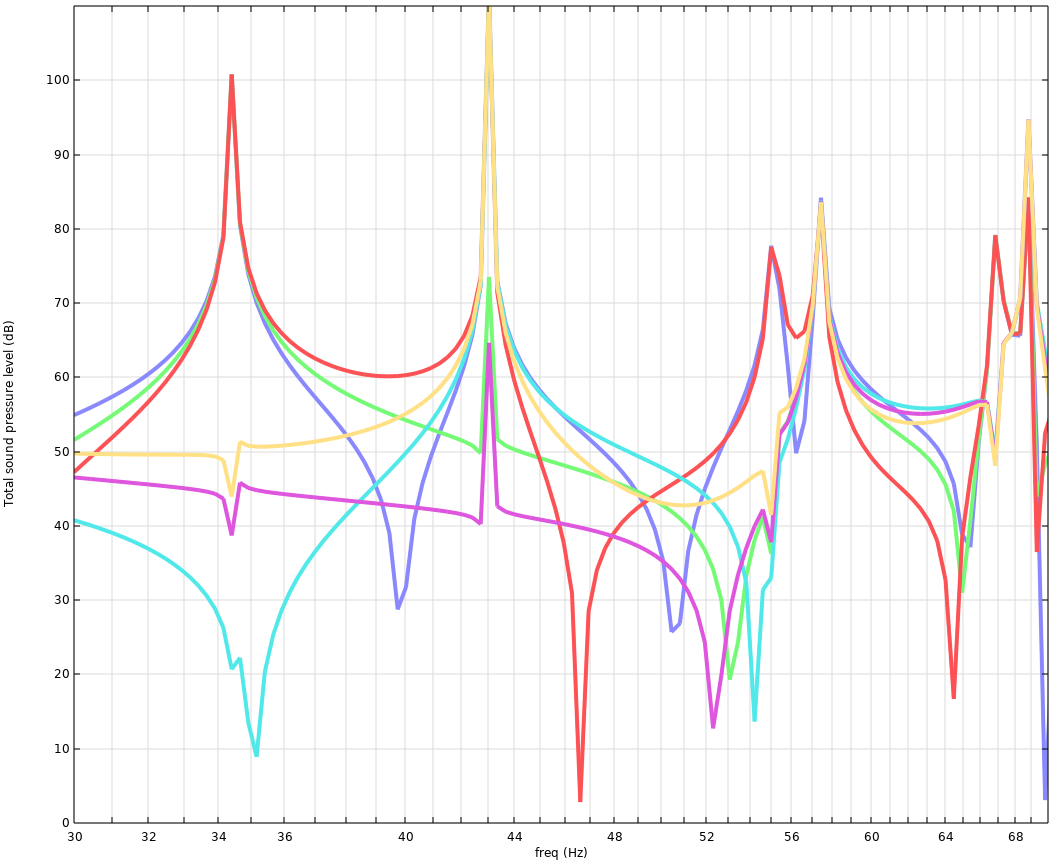
Some distinct issues can be seen at frequencies where there is a mode, but it would be wrong to say that a mode will always cause a resonance; that will depend on the source type and characteristics, and placement of both source(s) and your ears.
Many different multi-sub approaches could now be tried out but let us focus on the so-called Double Bass Array method. Here, the strategy basically is to turn the room into a tube. Tube acoustics is a little more involved than room acoustics (and a good topic if you want to really understand room acoustics better), but there is one major thing to understand: “The plane wave will always propagate”. Tube modes differ from room modes in that the former type really exist at all frequencies at once and will either propagate if excited above an associated modal frequency or die out as an evanescent wave below it. The only wave that will always propagate is the plane wave, and one way to achieve a propagating plane wave is to excite both the front wall and the rear wall in a pistonic-like fashion as shown in the animation below.

The front wall has its particular displacement, and the rear wall has a modified displacement to account for the phase shift coming from the wave travelling the room distance. You now effectively sit in an infinite tube with only a travelling wave and no reflection. Let us look at the response for this case.
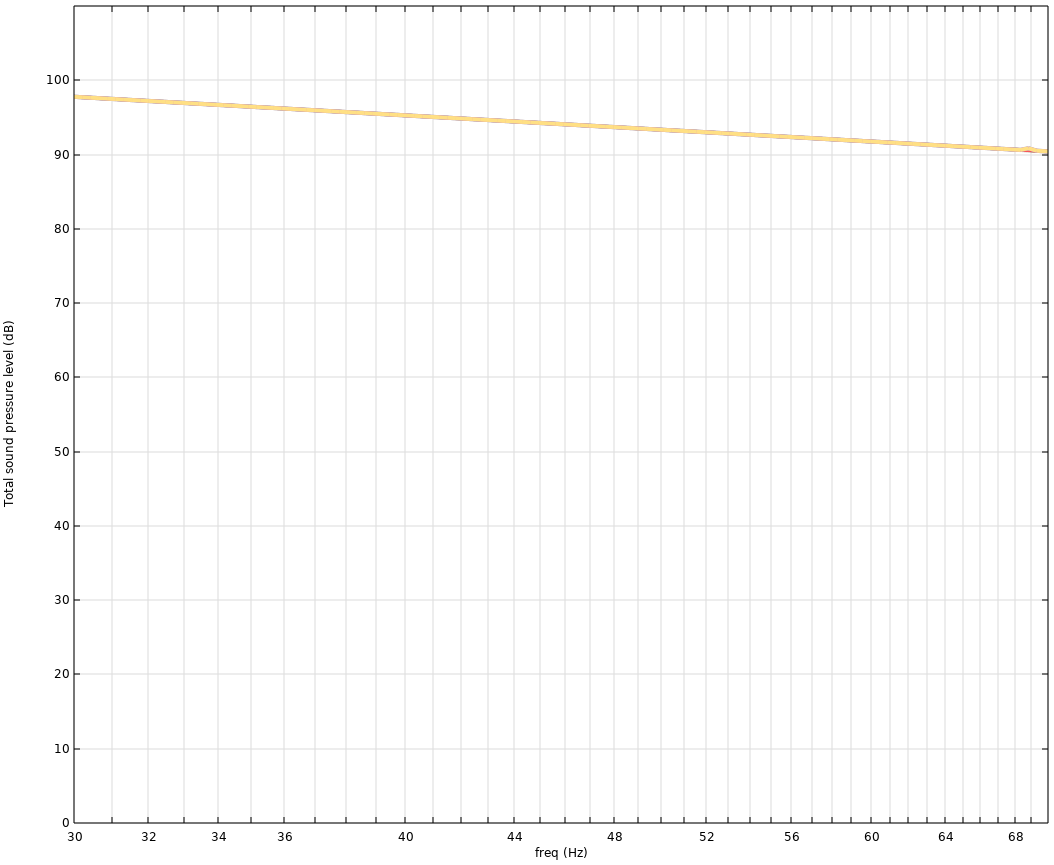
We have a one-dimensional sound field, with a travelling wave and no reflection. If the excitation is the entirety of the walls in a pistonic matter, this will be the case at all frequencies(!), no matter how high.
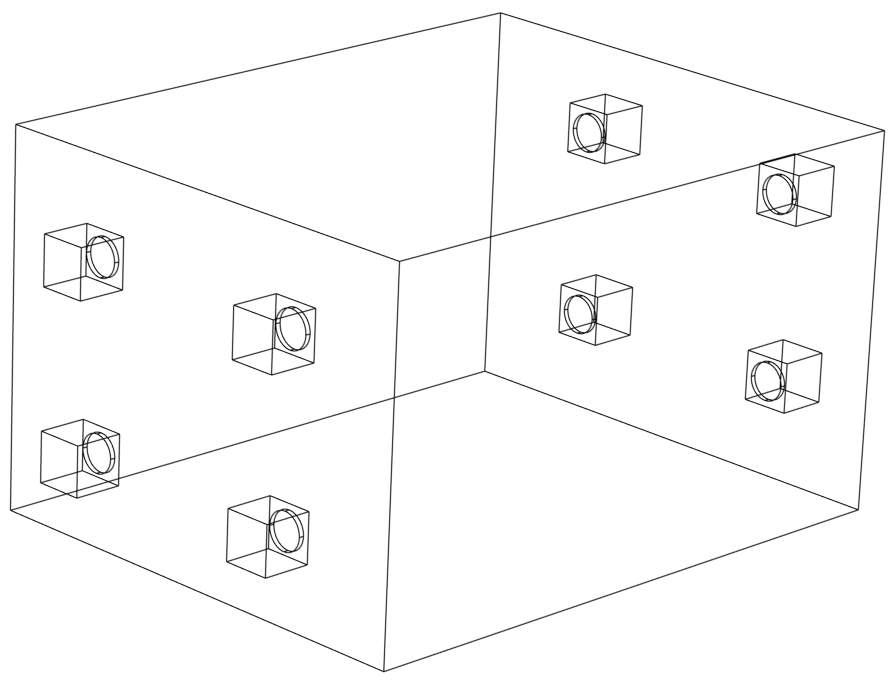
Now comes the practical implementation. With 4 subwoofers at the front wall, and 4 subwoofers at the rear wall with a phase modification to their response, a placement can be found that tries to emulate the full wall moving. Each driver sits 1/4 of the width/hight of the room away from the wall and are spaced 1/2 of that apart to have the mirror sources be spaced equally. We assume that the subwoofers are very flat or placed in the wall somehow as shown below.
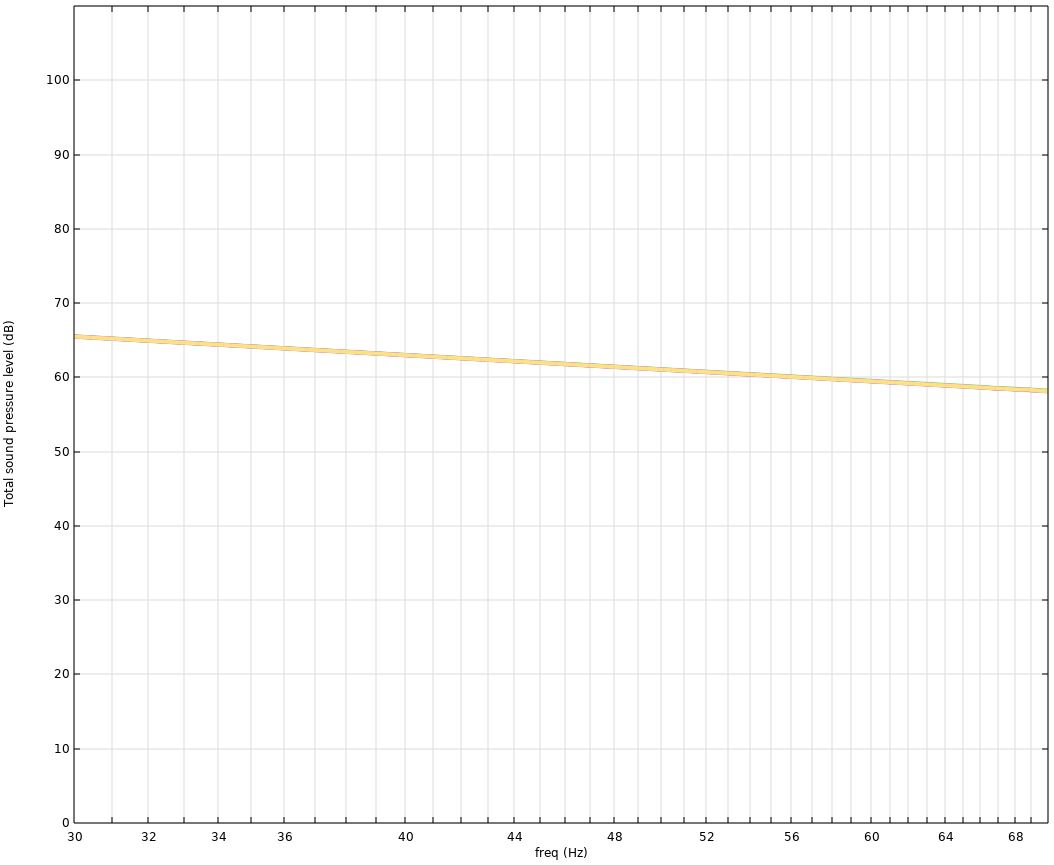
The corresponding responses actually look very good still at the low frequencies we are considering here.
With the simulation setup in place, you can now experiment away and for example investigate what happens if the four upper subwoofers are not connected.
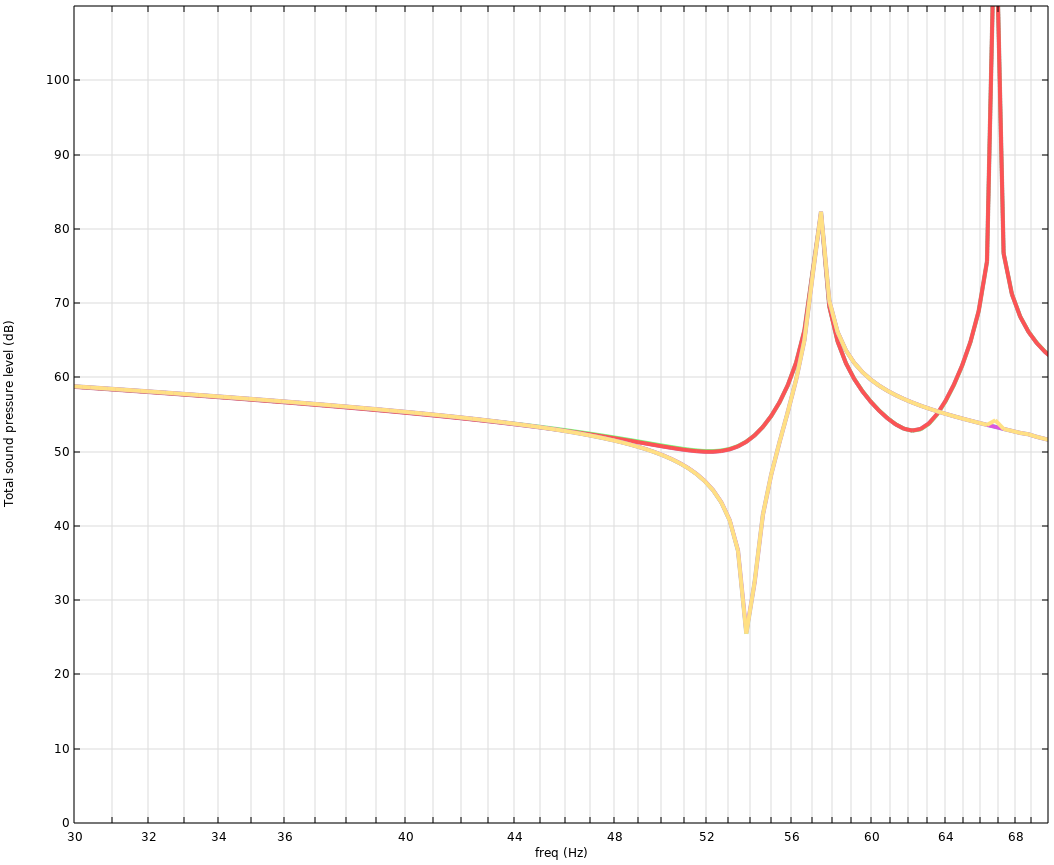
You could argue that they should be placed halfway up now, but I am going with this setup, since you probably have to place them near the floor in most situations anyway. In general, as you stray more and more away from the ‘walls moving’ situation, the response curves will naturally take a hit.
One can consider dropping the subwoofers at the rear wall and replace them with damping material. To investigate via simulations you will have to have some idea of that setup with damping material parameter and such.
You will need more than a phase knob
on your subwoofers to do this, as there is a time delay involved and that will not give you one phase for all frequencies, so some kind of DSP is needed.
Hopefully you have gotten the idea behind the DBA principle, and of course ask questions if something is not clear.
- About me -
René Christensen, Denmark, BSEE, MSc (Physics), PhD (Microacoustics), FEM and BEM simulations specialist in/for loudspeaker, hearing aid, and consultancy companies. Own company Acculution, blog at acculution.com/blog
Imagine first a 3x4x5 meters room. We can calculate the associated room modes as shown below.
These modes are an inherent feature of the room geometry and air being the medium inside it. They exist independent of any sources and are calculated without any regard to sourcing. Whether a mode is a problem or not will be evaluated when a source(s) is activated. Let us now put a subwoofer in the corner and evaluate the sound pressure level in 6 preselected places at a height of 1.1 meters.
The responses in the points vary quite a bit.
Some distinct issues can be seen at frequencies where there is a mode, but it would be wrong to say that a mode will always cause a resonance; that will depend on the source type and characteristics, and placement of both source(s) and your ears.
Many different multi-sub approaches could now be tried out but let us focus on the so-called Double Bass Array method. Here, the strategy basically is to turn the room into a tube. Tube acoustics is a little more involved than room acoustics (and a good topic if you want to really understand room acoustics better), but there is one major thing to understand: “The plane wave will always propagate”. Tube modes differ from room modes in that the former type really exist at all frequencies at once and will either propagate if excited above an associated modal frequency or die out as an evanescent wave below it. The only wave that will always propagate is the plane wave, and one way to achieve a propagating plane wave is to excite both the front wall and the rear wall in a pistonic-like fashion as shown in the animation below.
The front wall has its particular displacement, and the rear wall has a modified displacement to account for the phase shift coming from the wave travelling the room distance. You now effectively sit in an infinite tube with only a travelling wave and no reflection. Let us look at the response for this case.
We have a one-dimensional sound field, with a travelling wave and no reflection. If the excitation is the entirety of the walls in a pistonic matter, this will be the case at all frequencies(!), no matter how high.
Now comes the practical implementation. With 4 subwoofers at the front wall, and 4 subwoofers at the rear wall with a phase modification to their response, a placement can be found that tries to emulate the full wall moving. Each driver sits 1/4 of the width/hight of the room away from the wall and are spaced 1/2 of that apart to have the mirror sources be spaced equally. We assume that the subwoofers are very flat or placed in the wall somehow as shown below.
The corresponding responses actually look very good still at the low frequencies we are considering here.
With the simulation setup in place, you can now experiment away and for example investigate what happens if the four upper subwoofers are not connected.
You could argue that they should be placed halfway up now, but I am going with this setup, since you probably have to place them near the floor in most situations anyway. In general, as you stray more and more away from the ‘walls moving’ situation, the response curves will naturally take a hit.
One can consider dropping the subwoofers at the rear wall and replace them with damping material. To investigate via simulations you will have to have some idea of that setup with damping material parameter and such.
You will need more than a phase knob
on your subwoofers to do this, as there is a time delay involved and that will not give you one phase for all frequencies, so some kind of DSP is needed.
Hopefully you have gotten the idea behind the DBA principle, and of course ask questions if something is not clear.
- About me -
René Christensen, Denmark, BSEE, MSc (Physics), PhD (Microacoustics), FEM and BEM simulations specialist in/for loudspeaker, hearing aid, and consultancy companies. Own company Acculution, blog at acculution.com/blog
Last edited:

