neutralguy
Member
- Joined
- Apr 16, 2019
- Messages
- 68
- Likes
- 157
Published headphone measurements and Harman's target curve are derived based on measurements using a dummy head, with the intention that it represents an average of human heads. For people whose heads match the dummy's exactly, they should expect perfect Harman sound. What if my head isn't the same as the dummy's? HRTFs are known to vary among individuals, and the same headphone may exhibit different frequency responses for different people. To answer these questions, I used an in-ear microphone to measure my own HRTF and frequency response of headphones when actually mounted on my head.
To compute HRTF frequency response, I compared the frequency response of an in-ear microphone sitting in free space, versus the frequency response of the microphone when mounted in my ear. This difference will in general depend on the sound field, and the sound field I chose is that of the sweet spot of a stereo system with speakers separated by 30 degrees. This is basically the setup that would correspond to Harman's target curve, with some differences.
First is the dummy head versus my head and body. In fact, Harman's work was done on a Gras 45CA which doesn't even have a head. My speaker system is not equalized to be exactly flat, but as we see below that's fine for our purpose of headphone equalization. What's more important is the dispersion of the loudspeakers and the reflections in the room. In my case I used loudspeakers with even dispersion (Revel Salon2) in a large reverberant room. My measurements are taken at the entrance of the ear canal instead of at the eardrum, but that's ok as long as HRTF and headphone are both measured this way.
First, here is the computation of HRTF. The freestanding curve is the MS-TFB-2 in-ear microphone, dangling at a location roughly where my head would be, with its diaphragm facing forward. The in-ear curve is with the microphone inserted in my right ear. The sine sweep plays through the right speaker only. We're not concerned with crossfeed. The difference between these two curves is my right-ear HRTF. It is computed by dividing the traces in REW (subtraction in db is division). This "subtraction" has the beneficial side effect of canceling out the microphone's own response.
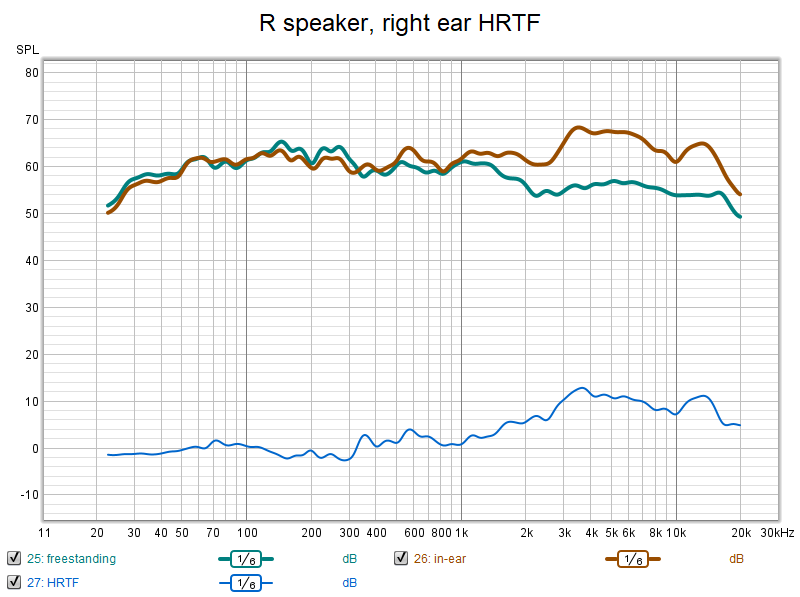
My HRTF appears consistent with the form of HRTFs found in the literature, even though most were derived from different sound fields. Most of them also show unevenness as we see here. In our case there may be extra unevenness due to quirks in the sound field caused by variations across frequencies in the reflectance of physical objects in the room.
Now we measure headphones using the same in-ear microphone. The AKG N60NC is a closed, on ear headphone with a 40mm driver behind an ear pad opening that is only about 25mm. The Philips SHP9500 is an open over ear headphone with a relatively large 50mm driver mounted at a slight angle like the Sennheiser HD800's.
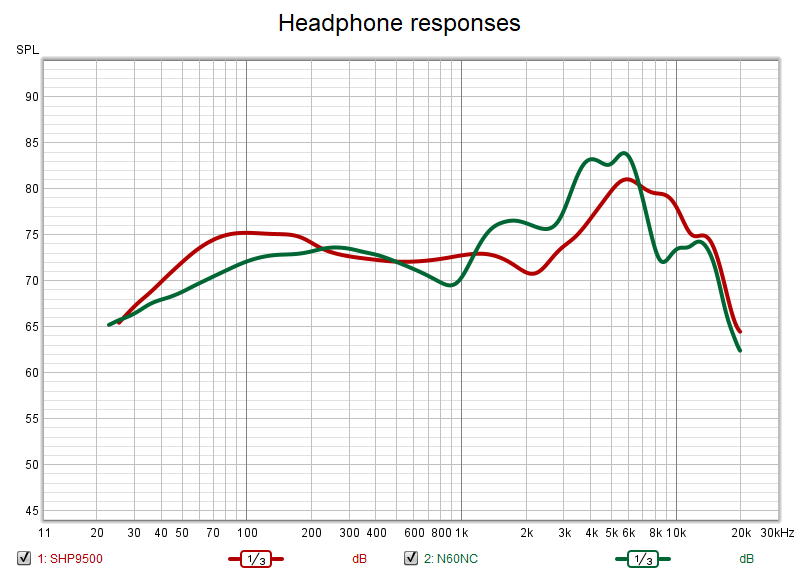
What we could do here is to equalize each curve to match the in-ear curve above, if we want our headphones to sound like our loudspeaker system. My loudspeaker system was not equalized flat except for bass, so even better would be to equalize to an idealized speaker response. To do this, we subtract the HRTF from the headphone response:
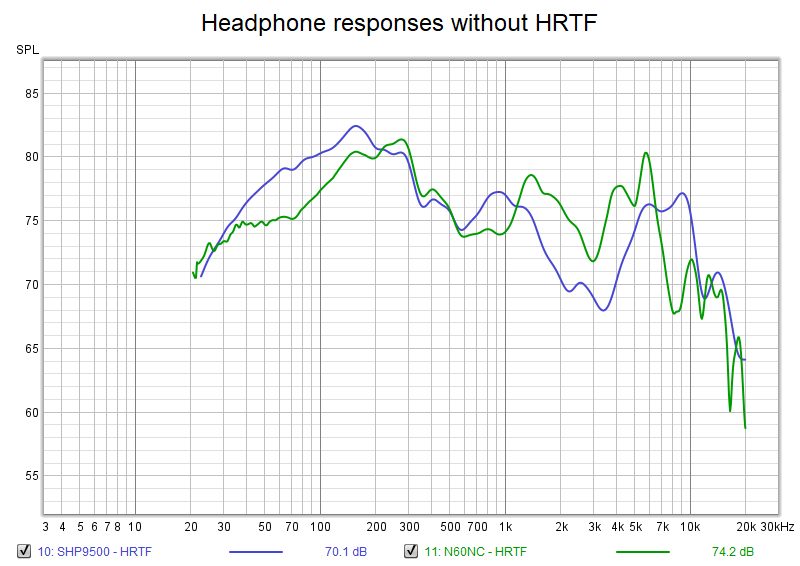
These curves are essentially the perceived in-room speaker responses to which each headphone's output corresponds. As in the Harman research, we roughly want this to be a line sloping downwards. I used a sloping line with a slight bass boost as the equalization target and equalized towards this idealized in-room response. REW has functionality to compute filters to match such a target. However, some of the peaks and dips here may be due to quirks in the measured HRTF, or to measurement artifacts such as the in-ear microphone's presence causing resonances or anti-resonances in the earcup that would not appear in usage. To be conservative I manually created broad (low Q) filters that match the target only broadly. Here's what it looks like for SHP9500:
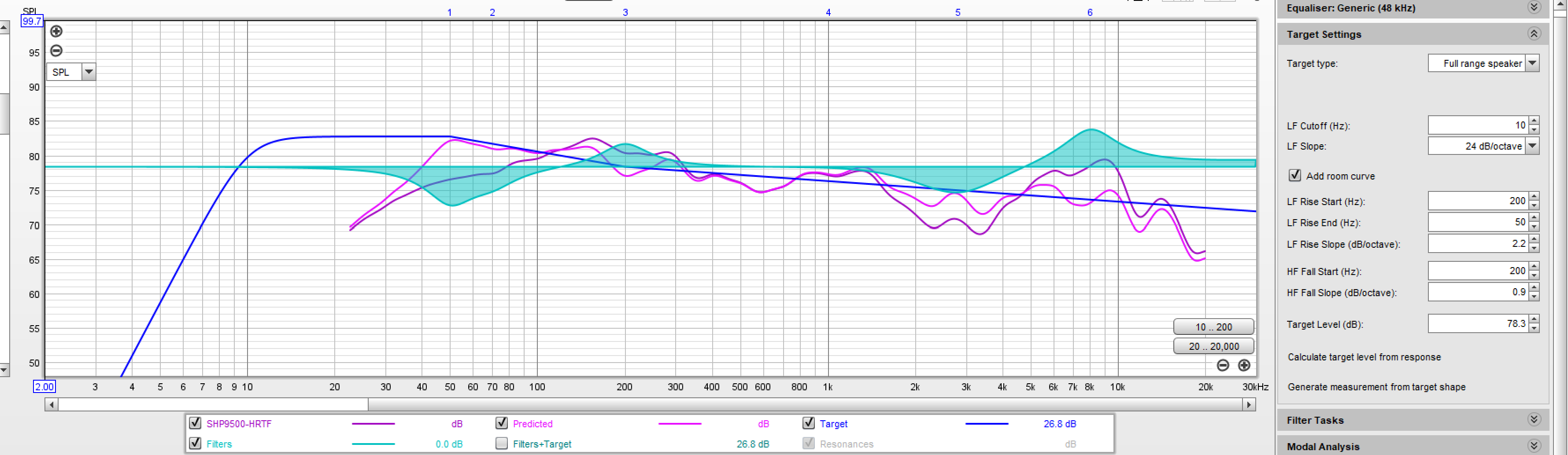
The resulting equalization settings are a definite improvement on the factory headphone sound to me. It made both headphones sound closer to the tonality of my speaker system and to each other.
In published measurements of SHP9500 on Rtings, the headphone shows good adherence to the Harman curve above 200hz, implying no eq should be used except in the bass. We see here that my own measurements disagree, and my subjective impressions agree with my measurements. Differences of this magnitude, such as a +5db Q=1 2800hz boost, is enough to turn a good sounding headphone into a bad one. I would think the difference owes largely to my HRTF being different from the dummy head's.
To get a sense of this variance, I measured another adult using the same procedure:
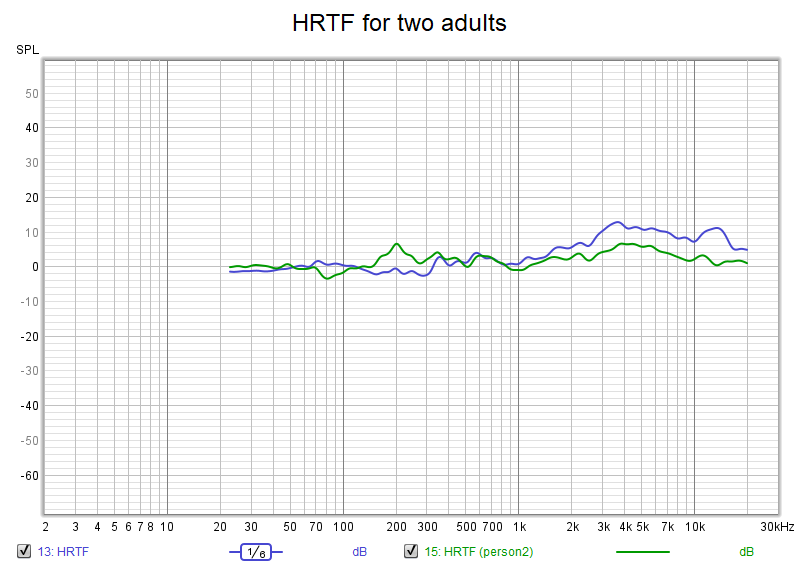
Confirming what we already know from the literature, HRTFs vary among individuals. The same headphone tuning cannot be ideal for all people.
Finally, to check the repeatability of the HRTF computation, I repeated the same measurements on my desktop speaker system to yield:
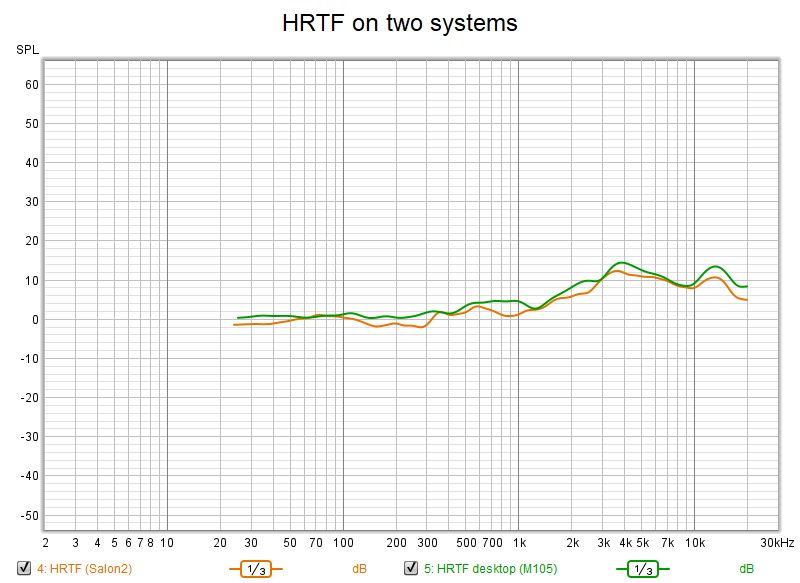
Differences are likely due to differences in sound fields, in the proportion of direct versus reflected sound in the desktop versus floorstander systems. The desktop speakers are in a smaller, less reverberant room, with the listening position an arms length away. There's also the reflective desk surface. If we had computed equalizations using the desktop's HRTF, we would end up with warmer eq settings. Indeed my desktop system sounds warmer than my main system even though both have roughly the same frequency response -- maybe the difference in HRTF is why.
Technical note 1: While we have factored out the mic's response from the HRTF curve, we have not done so for the headphone curves. To factor out the mic's response (assuming mic is uncalibrated), we can subtract its freestanding response from the response of a calibrated mic (e.g. UMIK1) to produce a mic correction curve. We then add this mic correction to the headphone measurements. I omitted the presentation of this step for simplicity. Alternatively, you can avoid this step by substituting a calibrated mic's response for "freestanding" in the HRTF computation.
Technical note 2: When doing trace arithmetic in REW, be sure to operate only on Averaged responses so it operates on magnitudes only.
TLDR
Using an in-ear microphone and loudspeaker system, I measured a personalized HRTF for my head and body. By measuring headphones on the same mic, I computed headphone equalizations corresponding to a personalized Harman target. The resulting equalizations are a subjective improvement to me over what would be derived from published measurements.
My main takeaway is that personalized equalization based on in-ear measurements works. It can improve the sound of even a headphone that measures well on a dummy head. The difference that personalization makes can be as large as that between good and bad sounding headphones.
To compute HRTF frequency response, I compared the frequency response of an in-ear microphone sitting in free space, versus the frequency response of the microphone when mounted in my ear. This difference will in general depend on the sound field, and the sound field I chose is that of the sweet spot of a stereo system with speakers separated by 30 degrees. This is basically the setup that would correspond to Harman's target curve, with some differences.
First is the dummy head versus my head and body. In fact, Harman's work was done on a Gras 45CA which doesn't even have a head. My speaker system is not equalized to be exactly flat, but as we see below that's fine for our purpose of headphone equalization. What's more important is the dispersion of the loudspeakers and the reflections in the room. In my case I used loudspeakers with even dispersion (Revel Salon2) in a large reverberant room. My measurements are taken at the entrance of the ear canal instead of at the eardrum, but that's ok as long as HRTF and headphone are both measured this way.
First, here is the computation of HRTF. The freestanding curve is the MS-TFB-2 in-ear microphone, dangling at a location roughly where my head would be, with its diaphragm facing forward. The in-ear curve is with the microphone inserted in my right ear. The sine sweep plays through the right speaker only. We're not concerned with crossfeed. The difference between these two curves is my right-ear HRTF. It is computed by dividing the traces in REW (subtraction in db is division). This "subtraction" has the beneficial side effect of canceling out the microphone's own response.
My HRTF appears consistent with the form of HRTFs found in the literature, even though most were derived from different sound fields. Most of them also show unevenness as we see here. In our case there may be extra unevenness due to quirks in the sound field caused by variations across frequencies in the reflectance of physical objects in the room.
Now we measure headphones using the same in-ear microphone. The AKG N60NC is a closed, on ear headphone with a 40mm driver behind an ear pad opening that is only about 25mm. The Philips SHP9500 is an open over ear headphone with a relatively large 50mm driver mounted at a slight angle like the Sennheiser HD800's.
What we could do here is to equalize each curve to match the in-ear curve above, if we want our headphones to sound like our loudspeaker system. My loudspeaker system was not equalized flat except for bass, so even better would be to equalize to an idealized speaker response. To do this, we subtract the HRTF from the headphone response:
These curves are essentially the perceived in-room speaker responses to which each headphone's output corresponds. As in the Harman research, we roughly want this to be a line sloping downwards. I used a sloping line with a slight bass boost as the equalization target and equalized towards this idealized in-room response. REW has functionality to compute filters to match such a target. However, some of the peaks and dips here may be due to quirks in the measured HRTF, or to measurement artifacts such as the in-ear microphone's presence causing resonances or anti-resonances in the earcup that would not appear in usage. To be conservative I manually created broad (low Q) filters that match the target only broadly. Here's what it looks like for SHP9500:
The resulting equalization settings are a definite improvement on the factory headphone sound to me. It made both headphones sound closer to the tonality of my speaker system and to each other.
In published measurements of SHP9500 on Rtings, the headphone shows good adherence to the Harman curve above 200hz, implying no eq should be used except in the bass. We see here that my own measurements disagree, and my subjective impressions agree with my measurements. Differences of this magnitude, such as a +5db Q=1 2800hz boost, is enough to turn a good sounding headphone into a bad one. I would think the difference owes largely to my HRTF being different from the dummy head's.
To get a sense of this variance, I measured another adult using the same procedure:
Confirming what we already know from the literature, HRTFs vary among individuals. The same headphone tuning cannot be ideal for all people.
Finally, to check the repeatability of the HRTF computation, I repeated the same measurements on my desktop speaker system to yield:
Differences are likely due to differences in sound fields, in the proportion of direct versus reflected sound in the desktop versus floorstander systems. The desktop speakers are in a smaller, less reverberant room, with the listening position an arms length away. There's also the reflective desk surface. If we had computed equalizations using the desktop's HRTF, we would end up with warmer eq settings. Indeed my desktop system sounds warmer than my main system even though both have roughly the same frequency response -- maybe the difference in HRTF is why.
Technical note 1: While we have factored out the mic's response from the HRTF curve, we have not done so for the headphone curves. To factor out the mic's response (assuming mic is uncalibrated), we can subtract its freestanding response from the response of a calibrated mic (e.g. UMIK1) to produce a mic correction curve. We then add this mic correction to the headphone measurements. I omitted the presentation of this step for simplicity. Alternatively, you can avoid this step by substituting a calibrated mic's response for "freestanding" in the HRTF computation.
Technical note 2: When doing trace arithmetic in REW, be sure to operate only on Averaged responses so it operates on magnitudes only.
TLDR
Using an in-ear microphone and loudspeaker system, I measured a personalized HRTF for my head and body. By measuring headphones on the same mic, I computed headphone equalizations corresponding to a personalized Harman target. The resulting equalizations are a subjective improvement to me over what would be derived from published measurements.
My main takeaway is that personalized equalization based on in-ear measurements works. It can improve the sound of even a headphone that measures well on a dummy head. The difference that personalization makes can be as large as that between good and bad sounding headphones.
