Theoretically Ideal DA Reconstruction

[MRC01]

Learning more about how DACs work, I read about the Whittaker-Shannon interpolation formula. I created a spreadsheet implementing that formula, so I could plug in some test sampling points and see the analog wave it constructs. I realized that each sampling point has a diminishing ripple that affects all its adjacent sampling points; to a decreasing extent as you get further away. This led to 2 realizations:

1. Any DAC that uses this method must read ahead. The spread of the ripple is symmetric in time, so to compute the amplitude of the analog wave at NOW, you need to know what are the sampling points in the future (and in the past).

2. Any DAC that uses this method must have considerable processing power. Because each sampling point affects the wave for thousands of sampling points both before and after it, to determine the analog amplitude at NOW, you must consider not just THIS sampling point, but also the influence of a few thousand samples both before and after this one.

Sanity check: for 16 bit samples, in the scenario of a full scale 0 dB sample, how many samples away does the ripple from this sample drop below the noise floor (-96 dB)? From the spreadsheet one can compute this to be about 22,000 samples. Thus a "perfect" DAC at 16 bit resolution must compute the influence of 44,000 samples for each sampling point (22,000 before & after) in order to ensure the amplitude at this point properly includes all ripple effects above the noise floor. I suspect it's only coincidence this is the CD sampling rate. To do this, the DAC must read ahead half a second, buffer 1 second of data, compute the sinc-t formula for all 44,000 samples in the buffer, each at the current sample time, and sum them.

It appears this ripple is where the Gibbs phenomenon comes from. It's neat to understand what causes this. It also shows that the ripple frequency is Nyquist, so it should be inaudible.

Does oversampling raise this Gibbs ripple frequency? It would seem that it does, but virtually all DACs oversample, and the analog waves I see from CD sources always show the Gibbs ripple at the same frequency.

I assumed DACs that have a standard "sharp" filter are using this method for DA reconstruction. But now that I see it requires so much read-ahead and processing power, I question whether this could be true. Or, perhaps they're estimating it with just a few samples before and after the current one, reducing the computational load, but having less than theoretically ideal performance.

This site won't let me upload the spreadsheet, but here's a picture. If there's a way to post the actual spreadsheet I'd appreciate any review of my formulas to ensure I got it right.

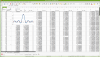
PS: I've also been reading about how R2R and DS DACs work. It seems the above sinc(t) stuff is only theoretical, not actually used. In case anyone is interested, here's the best explanation of DS I've found: https://www.beis.de/Elektronik/DeltaSigma/DeltaSigma.html. At first read I only understand half of it but a bit more might sink in over time.

 

[dc655321]

It's difficult to make out from your spreadsheet pic what you're calculating and how.

But now that I see it requires so much read-ahead and processing power, I question whether this could be true.

It is not
What you're describing (looking at past and future samples) is a system that violates causality (acausal).
DACs are not acausal.

It appears this ripple is where the Gibbs phenomenon comes from.

Yes and no? The ripple is a symptom of truncating the spectrum (band-limiting) of an input signal.
The ideal low-pass filter is a sinc function. By sampling a signal at frequency, fs, one is limiting the bandwidth of that system to fs/2.
In other words, the system has a brick-wall, low-pass filter at fs/2. Theoretically, this is a sinc function.

 

[MRC01]

I agree that the sinc(t) response to an impulse is acausal: the impulse has a pre-echo ripple before it hits. The Gibbs ripple preceding a square wave transition is the same thing. But I believe that DACs can be acausal: simple, just read ahead. You see this pre-echo in the output of many DACs.

Put differently: if DACs are acausal, how can they show a sinc(t) response around an impulse?

As I understand the theory, this pre-echo is the ideal reconstruction of the original analog wave. It's the closest you can get to the original analog signal, given the constraints of bandwidth limitation. No other way of constructing the wave can be better, alternatives are at best equal or worse fidelity overall. You can eliminate the pre-echo but in doing so you'll create more distortion somewhere else.

You can use a different reconstruction filter to avoid the pre-echo. There are many different options, some of which reduce or eliminate pre-echo. But the cure may be worse than the disease. The sinc(t) pre-echo rings at Nyquist so it should be inaudible. A minimum phase filter can eliminate pre-echo, but it rings longer and louder after the transient, and has extra phase distortion. Choose your poison! Here's a reference showing measurements of various alternative reconstruction filters. Most of them are acausal in that they have some pre-echo. http://archimago.blogspot.com/2013/06/measurements-digital-filters-and.html

 

[dc655321]

I agree that the sinc(t) response to an impulse is acausal

Not acausal. The sinc shape you see in the Archimago link is the impulse response of the filter (dac reconstruction).
i.e. put a Dirac delta through a system with a sinc function for an impulse response and the output produces that curve.

Maybe think of it this way - the samples all march one at a time through the sinc function, getting multiplied and accumulated (convolved), popping out the other side one at a time.

No need to read forward and backward in time.

As I understand the theory, this pre-echo is the ideal reconstruction of the original analog wave.

I suppose "ideal" is in the eye of the designer and device purpose, but what you're talking about is characteristic of a linear phase filter, meaning all frequencies are equally shifted (delayed), as opposed to a filter that shifts some frequencies more or less than others (eg: minimum phase). Sorry if you already know this...

 

[MRC01]

The sinc(t) function doesn't work one sample at a time. The amplitude of the analog wave at any given sample point is the infinite sum of all the sinc(t) pulses of every sample point. The S-W reconstruction algorithm has a simple appearance that belies its computational complexity.

Put differently, the S-W reconstruction algorithm is: plant a sinc(t) function centered at every sample point t, whose height is scaled to the sample value at t. Sum all of these together and you have your reconstructed wave. But that's not as easy as it sounds. Each sample point t is not just one value sinc(t) at that t, but a function defined over all time that ripples both forward and backward in time, affecting the values of every other sample. Its value is max at t itself, diminishes quickly as you get further away, but it never entirely goes to zero. Thus, to do the DA reconstruction using S-W, you must know every sample point before you reconstruct the first. Every other sample point has its own sinc(t) and no matter how far away it is (both future and past), it still has some influence on this one. You can't march them through one at a time.

That part above I'm pretty sure of, I worked out the math, built the spreadsheet, and it jives. But it's all theory. I have a lot of questions about how it works in practice:

There are different ways to do the DA reconstruction, which may allow marching samples through one at a time. From what I read, Delta Sigma is one such technique. However, since S-W is the theoretical ideal, the output accuracy of other techniques can be measured by how closely it resembles what you would get if you used the S-W algorithm.

I wonder if what Rob Watts at Chord is talking about with his DACs using banks of floating point processors, is computing this sinc(t)? To do it accurately you would need a DAC with lots of processing power and read-ahead.

All that said, the sinc(t) response to a single bit impulse ripples before the impulse happens, regardless of the algorithm used to construct it. Wouldn't you call this "acausal" regardless of what technique was used to produce it? Any pre-echo seems to be acausal by definition, no?

 

[dc655321]

Thus, to do the DA reconstruction using S-W, you must know every sample point before you reconstruct the first.

Nonsense.
You have experienced digital music playing before right? ;-)

You can't march them through one at a time.

That's how dacs work - they don't need to see all samples prior to producing any output.
If you feed a dac a single sample (eg: a 16 bit sample at 2^14, for a -6dB pulse), it will produce an output in response to that input.
You looked (I presume) at some examples of these impulse responses in the Archimago link you posted previously.

That part above I'm pretty sure of, I worked out the math, built the spreadsheet, and it jives.

You do seem pretty sure, but that's very different from having the right notions.

Functions defined over all time are not terribly practical, engineers tend to find ways around them.
And AFAIK, there are no devices that can peer into the future (think about digitizing a live musical signal, processing it, then D-A converting it back to analog for amplification to the audience's ears).

I wonder if what Rob Watts at Chord is talking about with his DACs using banks of floating point processors, is computing this sinc(t)?

He is talking about marching a single input sample through a bank FIR filter coefficients.
That filter could be an approximation of a sinc, truncated to finite length of course.
The longer the filter (more coefficients), the more resolution - the transition band can be made steeper (more brickwall-ish, ideal, etc).
This of course incurs delay in getting the input marched through the filter. The delay is (# of coeffs)/2 samples.

 

[MRC01]

Nonsense.
You have experienced digital music playing before right? ;-)
That's how dacs work - they don't need to see all samples prior to producing any output. ...

I didn't say all DA reconstruction works like this. I said the S-W algorithm works like this. DACs don't necessarily use the S-W algorithm. I mentioned learning about alternative algorithms that would not need to do this, and their output may approach the ideal response that S-W produces.

...
Functions defined over all time are not terribly practical, engineers tend to find ways around them.
And AFAIK, there are no devices that can peer into the future (think about digitizing a live musical signal, processing it, then D-A converting it back to analog for amplification to the audience's ears).

Of course, that's what I'm saying.
BTW, "looking into the future" is simple: just buffer with a delay. You can do this AD and DA. Again, I'm not saying all algorithms must do this. It's necessary if you're going to use the S-W formula, but there may be alternatives that don't require it.

...
He is talking about marching a single input sample through a bank FIR filter coefficients.
That filter could be an approximation of a sinc, truncated to finite length of course.
The longer the filter (more coefficients), the more resolution - the transition band can be made steeper (more brickwall-ish, ideal, etc).
This of course incurs delay in getting the input marched through the filter. The delay is (# of coeffs)/2 samples.

Exactly!
But as I read, alternative algorithms like delta-sigma produce output that is the same for all practical purposes, without the need for look-ahead, delays, and floating point computations. Theorists like Shannon discover the ideal and if it's impractical, engineers find a pragmatic way to get nearly the same thing a lot easier.
I find Watt's approach interesting from an academic perspective, but I wonder why spend all that extra complexity and cost doing it the theoretically "pure" way if alternative algorithms are faster and easier, and produce the same output?
Of course, audiophiles debate whether the output really is "the same"...

 

[mansr]

A mathematically perfect reconstruction would require a sinc filter extending to infinity in both directions. On the face of it, this is impossible to realise since, as has been noted, to produce even one output sample, we'd need to look ahead to the end of time.

However, with a finite-length input, such as a music track, each output sample is the sum of a finite number of sinc functions. The output still has infinite length, but we only care about a segment of equal duration to the input. This is something we can actually calculate. The scale of these computations is somewhat unpractical, yet not impossible for a modern desktop computer. For a DAC being fed a stream of unknown duration, this is still, of course, of no help. It would have to buffer all the data until someone presses the stop button before it could emit the slightest blip. Besides it being unpractical, if not impossible, to construct such a device, nobody would want it.

We shouldn't give up yet, though. Since there is a non-zero noise level in our analogue electronics, and even in air itself, we don't actually require the infinite precision the reasoning above was based on. This means an approximation of the sinc function will work as long as the error is below whatever threshold we decide is acceptable. The most obvioux approximation is to simply truncate the sinc function where its level drops so low that the contribution is below the noise level. With this approach, good results can be had from a filter with a length of a few million samples. While this brings us within the realm of the practical for a desktop computer, it is still too much to ask of a tiny DAC chip.

Thankfully, we can do one more approximation. The perfect sinc filter is infinitely steep, its frequency response dropping from 100% to zero in an instant. This is also something we do not need. Even at 44.1 kHz sample rate, allowing a transition band of 1 kHz will make no discernible difference. This modified response can be achieved with a filter length of only a few thousand (or even a few hundred) samples. That's something even a small chip can do.

This leaves us with the issue of causality. Even the simplified filters discussed above are centred around time zero. That is, they require access to future input samples, and chip-scale crystal balls are not yet a reality. Recall, however, that these filters have finite length. This means that if we shift them suitably along the time axis, they become zero-valued for negative time values. After the convolution process, this translates to a time delay of the output equal to the shift of the filter function.

In summary, a well-performing DAC can be constructed with the only penalty being a delay of a few thousand samples. If that is too much, we have to resort to minimum phase filters, but that is a topic for another day.

 

[MRC01]

.... Since there is a non-zero noise level in our analogue electronics, and even in air itself, we don't actually require the infinite precision the reasoning above was based on. This means an approximation of the sinc function will work as long as the error is below whatever threshold we decide is acceptable. The most obvioux approximation is to simply truncate the sinc function where its level drops so low that the contribution is below the noise level. ...

Yes, and for the W-S formula, at 16-bit precision that's about 22,000 samples in each direction. At CD rates that is about 1 second and seems feasible.

...
In summary, a well-performing DAC can be constructed with the only penalty being a delay of a few thousand samples. If that is too much, we have to resort to minimum phase filters, but that is a topic for another day.

Thanks!

 

[andreasmaaan]

Yes, and for the W-S formula, at 16-bit precision that's about 22,000 samples in each direction. At CD rates that is about 1 second and seems feasible.

Thanks!

I'm no expert, but wouldn't the only advantage offered by the kind of filter you're describing be outside of the audio band anyway?

So, if concerned about a non-perfect filter having an audible impact, why not just increase the sample rate to some frequency that assuages one's audio nervosa?

Interesting discussion though, thanks for getting it going.

 

[dc655321]

Sorry @MRC01, I lost sight of your focus on the theoretical in trying to explain how/why digital conversion works in practice.
Theories are of course the basis, but practicalities and real-world approximations are just as interesting (and, you know, useful!).
I appreciate your curiosity and initiative in working things out for yourself.

 

[MRC01]

I'm no expert, but wouldn't the only advantage offered by the kind of filter you're describing be outside of the audio band anyway?

So, if concerned about a non-perfect filter having an audible impact, why not just increase the sample rate to some frequency that assuages one's audio nervosa? ...

Here's what I find interesting about it (S-W reconstruction formula): it doesn't change the dots, it changes how you connect the dots.

More precisely, the sinc(t) function passes through exactly zero at every sampling point except the one at which it's centered (incidentally, this also means it "rings" at exactly the Nyquist frequency and should be inaudible in and of itself). So if it's zero at every sampling point except its center, and it rings at Nyquist which is inaudible, how can it affect reconstruction at those other points? Because it changes the shape of the analog wave between the sampling points!

You can draw an infinite number of different analog waves that pass through all the sampling points. But once you bandwidth limit your analog wave to contain only frequencies below Nyquist, there is 1 and only 1 unique analog wave that passes through these sampling points. The S-W formula perfectly reconstructs exactly that wave.

So if you follow the S-W formula but you only use N adjacent samples instead of all of them, then the analog wave you construct will not reflect the influence of sampling points further away than N. Thus, the shape it follows between the sampling points will not be the same. In the frequency domain, it means you are allowing a (small) amount of energy above Nyquist to leak through. This is the same as saying your filter has a more gradual slope. This may allow passband distortion, in the form of aliased artifacts from those frequencies.

All in theory, of course. Whether the differences are measurable or audible to humans is an engineering question. After this study and implementing the formula in a spreadsheet I feel like I have a good handle on the theory. It's the engineering side that I need to learn more about: alternative reconstruction methods, measurable or audible tradeoffs, etc. What's been most useful about this discussion is that I didn't realize at first that nobody* actually implements the S-W formula. Instead they use alternative methods that are more practical to implement and provide similar results.
* except perhaps for Rob Watts of Chord!

 

[andreasmaaan]

You can draw an infinite number of different analog waves that pass through all the sampling points. But once you bandwidth limit your analog wave to contain only frequencies below Nyquist, there is 1 and only 1 unique analog wave that passes through these sampling points. The S-W formula perfectly reconstructs exactly that wave.

I'm going to bow out here because I'm not adequately knowledgeable to contribute more, but my only thought at this point is that for non-SW reconstruction filters, if they are well-designed, any deviations from the original waveform will not occur at frequencies below the transition band (and therefore will not affect the audio band). Perhaps someone who knows more can tell me if I'm right on this?