<This is a repost of an old thread on a timeless subject.>
Comb filter effects are a popular topic of discussion among audiophiles (and many others, of course). However, some audiophiles may not have a good concept of what they look like, why they may (or may not) be bad, and what they can do about them. Or even if they have them and need to do anything about them.
Picture the signal from the speaker as a single sine wave. Two, speakers, two sound waves. If they are in phase, then adding them together simply doubles the amplitude at every point. If you have two speakers playing the same signal at the same level, and are equidistant from them, then you will hear the signal twice as loudly as if a single speaker was playing. Or will you? It’s complicated…
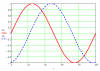
The figure below shows two 1 kHz sine waves generated by two speakers, but one is 3” further away from the listener. The red line is from the closer speaker and the dashed blue line is the signal from the farther speaker. Clearly there is a difference in phase between the two signals, and if we add them together at each point in time (t is relative in this plot), we will not get a doubling in amplitude.
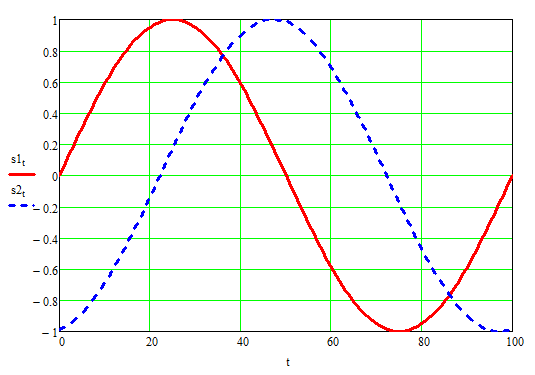
Remember wavelength is related to frequency and lower frequencies have longer wavelength. If we change the frequency to 100 Hz, there is less phase shift, since the distance is smaller compared to the wavelength. Their sum would still not quite double, but it would be close.
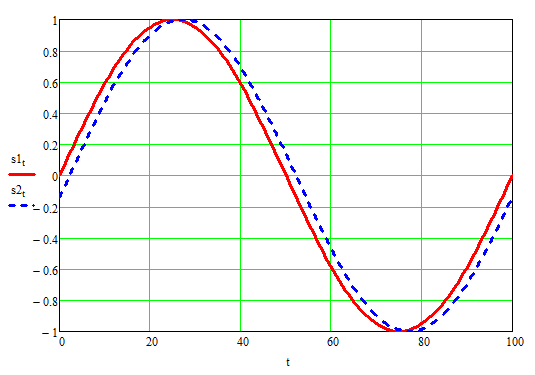
Take that same 3” difference and look at 2 kHz, and now the waves are nearly 180 degrees shifted in phase. Add them together and they will nearly completely cancel. Ouch!
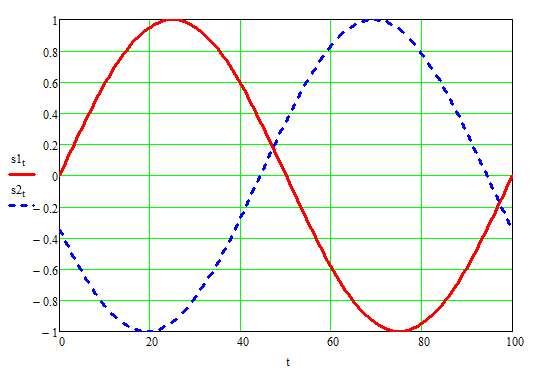
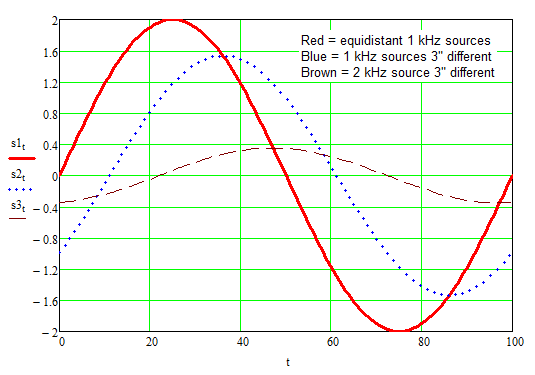
So, if there is a path difference between two speakers, and we sum their outputs at the listening position, what we hear depends upon the difference in distance and the frequency. The figure below shows three plots: red is two identical 1 kHz signals summed from two equidistant speakers, dotted blue is the result when one speaker is 3” farther away, and dashed brown is the result with the same 3” difference in distance but at 2 kHz. You can clearly see how the amplitude changes.
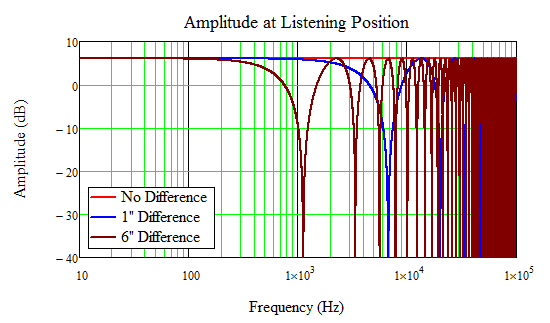
OK, so if we sweep frequency, what happens? At different frequencies the signals will add in phase, out of phase, or someplace in between. In phase, we expect the signal to double, a 6 dB increase. Completely (180 degrees) out of phase, they will cancel –infinity dB). Now we know the amplitude will depend upon both the frequency and difference in distance to the listener. Below shows the response from two identical sources (dark green), the result when one is just 1” further away (blue), and when one is 6” further away (red). You can see the dips in frequency when the difference in distance causes the signals to cancel at the listening position.
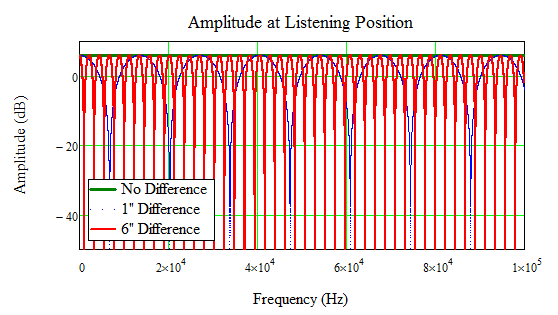
Why “comb filter”? Look at the same plot but using linear (even) frequency steps instead of the logarithmic plot we are used to seeing. Looks like a comb, yes? Whenever the distance is such that the signal from the two speakers is out of phase, then you will get another tine on the comb where the signal cancels and amplitude drops to 0 (-infinite dB).
Now, the signal is completely out of phase when the distance shifts the signal one-half the period of sine wave. Since sound travels at about 1127’/s (standard conditions), then the first dip or tine will happen at
Frequency of first dip = (difference in distance in feet) / (1127’/s * 1/2)
So 1” means the first dip (tine) is around 6.8 kHz, and 6” difference means the first dip is around 1.127 kHz. The dips occur at odd multiples (3, 5, 7…) after that, so for 6” we see dips at 1.1 kHz, 3.4 kHz, 5.6 kHz, and so forth. At even multiples the signal is back in phase with the original and does not cancel.
Do you have comb filtering? Well, yes, no matter how well-treated your room might be. There are several things that can cause comb filter effects:
One of the “other path differences” that happens in the real world is the space between our ears. Not our brains, though that is important, but the distance from one ear to the other. If your ears are 6” apart, then you hear the signal from one speaker the equivalent of 6” “later” than the signal from the other, thus creating your own little comb filter. Toole and many others have discussed this and its impact. It is easily calculated, and/or measured, but there is some debate its impact. Some argue this is a fundamental problem with stereo speakers and there is no way around it; others claim our brain processes the two signals, accounts for the delay, and so we do not really “hear” the dips. When I measure and listen, I can easily hear the comb filter effects from the rear wave of my dipoles (more on that later), and hear how they are gone when I absorb the rear wave, but do not seem to hear dips from a mono signal played from two speakers. I could easily be fooling myself, of course, since I know what I am feeding the speakers and how they are set up. See previous psychoacoustics disclaimer and note I have not kept up in that area (maybe when I retire).
I do not want to get into that debate, but can delve into reflections. Reflections add a couple of variable not discussed so far:
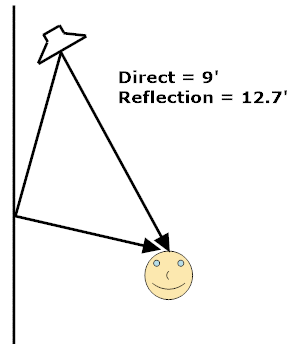
Consider a single speaker 9’ away from the listener with a wall a couple of feet away. The reflected path is about 12.7’ long, and the signal inverts at the boundary (wall). The resulting frequency response is shown in the next plot. The first null is at 304 Hz and they occur at every (not just odd) frequency multiple upwards (due to the phase inversion from the reflection). Also note that at very low frequencies the response is impacted by the signal interactions, reducing LF response. What this does not show is the impact of the extra delay on the signal. The path difference of 3.7’ is a time delay of about 3.3 ms. See Haas Effect (https://en.wikipedia.org/wiki/Precedence_effect) to see how we might resolve the delay (we typically do not perceive single events 1 ~ 5 ms apart as a separate sound, and up to perhaps 40 ms for more complex signals like music, though arguments have been made about “smearing” of the signal).
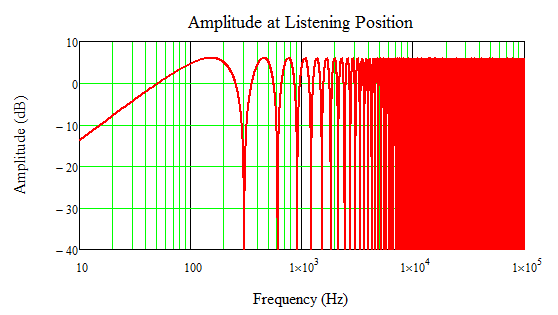
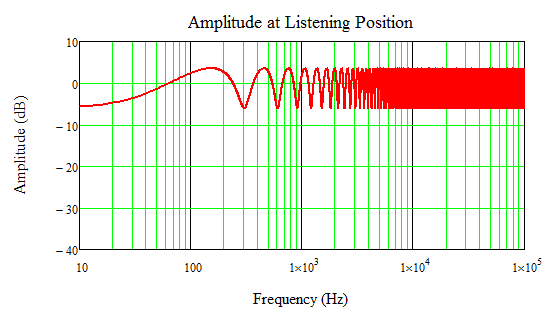
Adding broadband absorption to reduce the reflected amplitude by half (6 dB) significantly reduces the null depth. This is one of the arguments for absorption in the listening room. Real absorbers are not flat across frequency, of course, so a more realistic plot would show less change at low frequencies and much more at high frequencies, reducing high-frequency ripples to negligible (i.e. small in amplitude and close together so more readily masked by adjacent signals with actual source material).
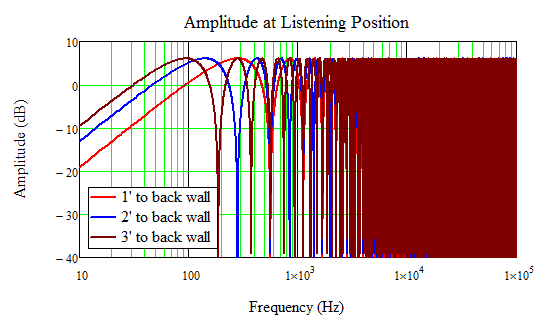
Since I own dipoles, there is one last set of plots worth showing. The next figure shows how the response changes as you move a dipole speaker from the back wall. The frequency of the first null drops, of course, due to the longer path length. Again Hass Effect enters into the audibility since the delay also increases with distance, and the reflection will be somewhat attenuated in the real world.
How much comb effects matter is subject to psychoacoustics, something outside my field. Please start another thread to discuss that; this is just to present the background and examples. What should be clear is they exist in every system in one form or another, both distance and frequency determine their nature, and that absorption can reduce some of them (desirable or not). Diffusion can also reduce them by decorrelating (scattering) the waves so they do not recombine significantly. Diffusion preserves much of the energy so the room is not as “dead” so many people may prefer that sound.
Comb filter effects are a popular topic of discussion among audiophiles (and many others, of course). However, some audiophiles may not have a good concept of what they look like, why they may (or may not) be bad, and what they can do about them. Or even if they have them and need to do anything about them.
Picture the signal from the speaker as a single sine wave. Two, speakers, two sound waves. If they are in phase, then adding them together simply doubles the amplitude at every point. If you have two speakers playing the same signal at the same level, and are equidistant from them, then you will hear the signal twice as loudly as if a single speaker was playing. Or will you? It’s complicated…
The figure below shows two 1 kHz sine waves generated by two speakers, but one is 3” further away from the listener. The red line is from the closer speaker and the dashed blue line is the signal from the farther speaker. Clearly there is a difference in phase between the two signals, and if we add them together at each point in time (t is relative in this plot), we will not get a doubling in amplitude.
Remember wavelength is related to frequency and lower frequencies have longer wavelength. If we change the frequency to 100 Hz, there is less phase shift, since the distance is smaller compared to the wavelength. Their sum would still not quite double, but it would be close.
Take that same 3” difference and look at 2 kHz, and now the waves are nearly 180 degrees shifted in phase. Add them together and they will nearly completely cancel. Ouch!
So, if there is a path difference between two speakers, and we sum their outputs at the listening position, what we hear depends upon the difference in distance and the frequency. The figure below shows three plots: red is two identical 1 kHz signals summed from two equidistant speakers, dotted blue is the result when one speaker is 3” farther away, and dashed brown is the result with the same 3” difference in distance but at 2 kHz. You can clearly see how the amplitude changes.
OK, so if we sweep frequency, what happens? At different frequencies the signals will add in phase, out of phase, or someplace in between. In phase, we expect the signal to double, a 6 dB increase. Completely (180 degrees) out of phase, they will cancel –infinity dB). Now we know the amplitude will depend upon both the frequency and difference in distance to the listener. Below shows the response from two identical sources (dark green), the result when one is just 1” further away (blue), and when one is 6” further away (red). You can see the dips in frequency when the difference in distance causes the signals to cancel at the listening position.
Why “comb filter”? Look at the same plot but using linear (even) frequency steps instead of the logarithmic plot we are used to seeing. Looks like a comb, yes? Whenever the distance is such that the signal from the two speakers is out of phase, then you will get another tine on the comb where the signal cancels and amplitude drops to 0 (-infinite dB).
Now, the signal is completely out of phase when the distance shifts the signal one-half the period of sine wave. Since sound travels at about 1127’/s (standard conditions), then the first dip or tine will happen at
Frequency of first dip = (difference in distance in feet) / (1127’/s * 1/2)
So 1” means the first dip (tine) is around 6.8 kHz, and 6” difference means the first dip is around 1.127 kHz. The dips occur at odd multiples (3, 5, 7…) after that, so for 6” we see dips at 1.1 kHz, 3.4 kHz, 5.6 kHz, and so forth. At even multiples the signal is back in phase with the original and does not cancel.
Do you have comb filtering? Well, yes, no matter how well-treated your room might be. There are several things that can cause comb filter effects:
- Two speakers not equidistant to the listener;
- Variations in speakers or other components that cause phase differences in the signal path;
- Reflected signals adding to the main signals;
- Other path differences that induce delays between the two sources.
One of the “other path differences” that happens in the real world is the space between our ears. Not our brains, though that is important, but the distance from one ear to the other. If your ears are 6” apart, then you hear the signal from one speaker the equivalent of 6” “later” than the signal from the other, thus creating your own little comb filter. Toole and many others have discussed this and its impact. It is easily calculated, and/or measured, but there is some debate its impact. Some argue this is a fundamental problem with stereo speakers and there is no way around it; others claim our brain processes the two signals, accounts for the delay, and so we do not really “hear” the dips. When I measure and listen, I can easily hear the comb filter effects from the rear wave of my dipoles (more on that later), and hear how they are gone when I absorb the rear wave, but do not seem to hear dips from a mono signal played from two speakers. I could easily be fooling myself, of course, since I know what I am feeding the speakers and how they are set up. See previous psychoacoustics disclaimer and note I have not kept up in that area (maybe when I retire).
I do not want to get into that debate, but can delve into reflections. Reflections add a couple of variable not discussed so far:
- When a signal hits a boundary and reflects, the reflected wave is inverted from the original wave; and,
- Unless the boundary is a perfect reflector there will be some attenuation of the reflected wave.
Consider a single speaker 9’ away from the listener with a wall a couple of feet away. The reflected path is about 12.7’ long, and the signal inverts at the boundary (wall). The resulting frequency response is shown in the next plot. The first null is at 304 Hz and they occur at every (not just odd) frequency multiple upwards (due to the phase inversion from the reflection). Also note that at very low frequencies the response is impacted by the signal interactions, reducing LF response. What this does not show is the impact of the extra delay on the signal. The path difference of 3.7’ is a time delay of about 3.3 ms. See Haas Effect (https://en.wikipedia.org/wiki/Precedence_effect) to see how we might resolve the delay (we typically do not perceive single events 1 ~ 5 ms apart as a separate sound, and up to perhaps 40 ms for more complex signals like music, though arguments have been made about “smearing” of the signal).
Adding broadband absorption to reduce the reflected amplitude by half (6 dB) significantly reduces the null depth. This is one of the arguments for absorption in the listening room. Real absorbers are not flat across frequency, of course, so a more realistic plot would show less change at low frequencies and much more at high frequencies, reducing high-frequency ripples to negligible (i.e. small in amplitude and close together so more readily masked by adjacent signals with actual source material).
Since I own dipoles, there is one last set of plots worth showing. The next figure shows how the response changes as you move a dipole speaker from the back wall. The frequency of the first null drops, of course, due to the longer path length. Again Hass Effect enters into the audibility since the delay also increases with distance, and the reflection will be somewhat attenuated in the real world.
How much comb effects matter is subject to psychoacoustics, something outside my field. Please start another thread to discuss that; this is just to present the background and examples. What should be clear is they exist in every system in one form or another, both distance and frequency determine their nature, and that absorption can reduce some of them (desirable or not). Diffusion can also reduce them by decorrelating (scattering) the waves so they do not recombine significantly. Diffusion preserves much of the energy so the room is not as “dead” so many people may prefer that sound.