- Joined
- Feb 23, 2016
- Messages
- 20,759
- Likes
- 37,612
http://audiosciencereview.com/forum...ements-of-mytek-brooklyn-dac.1828/#post-46082
Ray was looking at a test signal I suggested for the Mytek Brooklyn review thread starting with the above post.
It is a test signal Juergen Reis of MBL suggested to JA of Stereophile. It is - 4dbFS of white noise played at a lower sample rate and measured at a much higher sample rate. The idea is the residual noise above nyquist of the original signal will reveal the shape/steepness of the anti-imaging filter on the DAC output.
Ray upsampled such a signal by 8x to better see the waveshape between samples as I had mentioned such a signal clipped an ADC at lower levels than a -.1 dbFS sine wave. Ray surmised these were intersample overs which seems reasonable. A question in my mind was whether such signals were showing us accurately the imaging filter shape or was it ultrasonic noise from the slight clipping. In upsampled signals the level of ultrasonic noise was higher if the original was -4 db FS than if it was -6 db FS by a pretty large amount. The ultrasonic noise was very high for a 0 dbFS white noise signal when upsampled. Now all of this was in software I should mention. Another question was whether upsampling playback software clipped such signals.
Some DACs have been known to have inadequate analog headroom for intersample overs and to have some clipping from that. I suspect that is why Reis chose - 4db as most well designed gear is not going to have an issue with a signal at that level in the analog output stage.
So I used an old Tact RCS 2.0 set unity gain to playback these signals at 48 khz, and recorded them at 192 khz with a Focusrite Forte. I should mention this is 93.9 on the Tact volume control as it applies digital gain above that level up to 99.9 settings. So this is no digital volume adjustment. I set input levels as high as possible on the Forte ADC as long as it did not indicate clipping. I had signals starting at 0 dbFS and going in 1 db steps to -7 dbFS.
To shorten the story, I found the intersample levels not to cause any clipping in the DAC done this way and the resulting FFT does appear to show the shape of the anti-imaging filter of the DAC. Also I found if I adjusted levels so that - 4db was also nearly, but not clipping the ADC input, the resulting noise profile was virtually identical to 0 db. Without resetting gain the shape of the response was the same at all levels other than being lower by 1 db each progression thru the test signal.
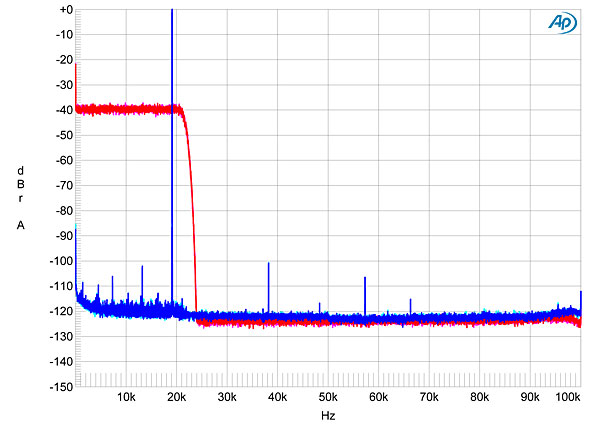
Here is the shape of the 0 dbFS noise signal in red, the gain adjusted - 4dbFS signal in green, and the silent noise floor in blue.
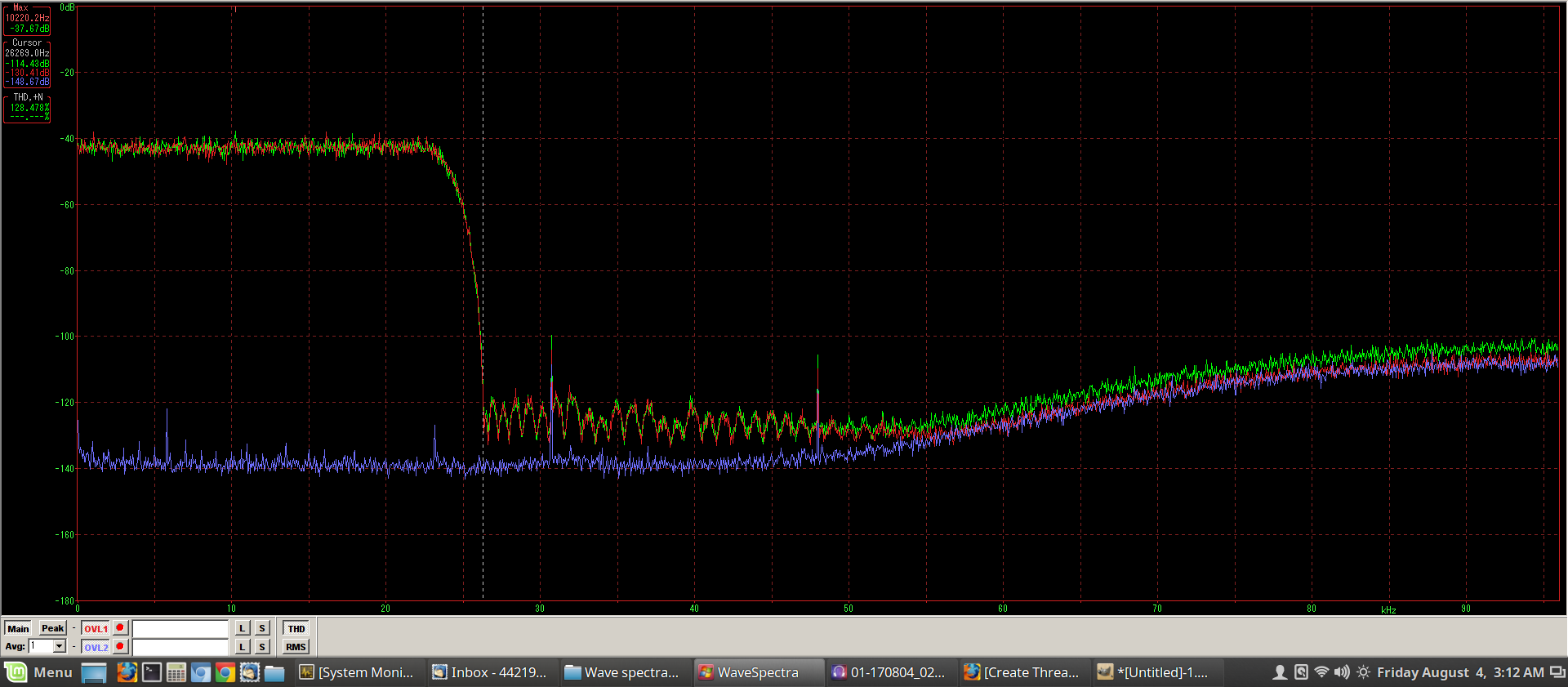
Here is the same comparison using a Focusrite 18i20 interface in place of the Tact.
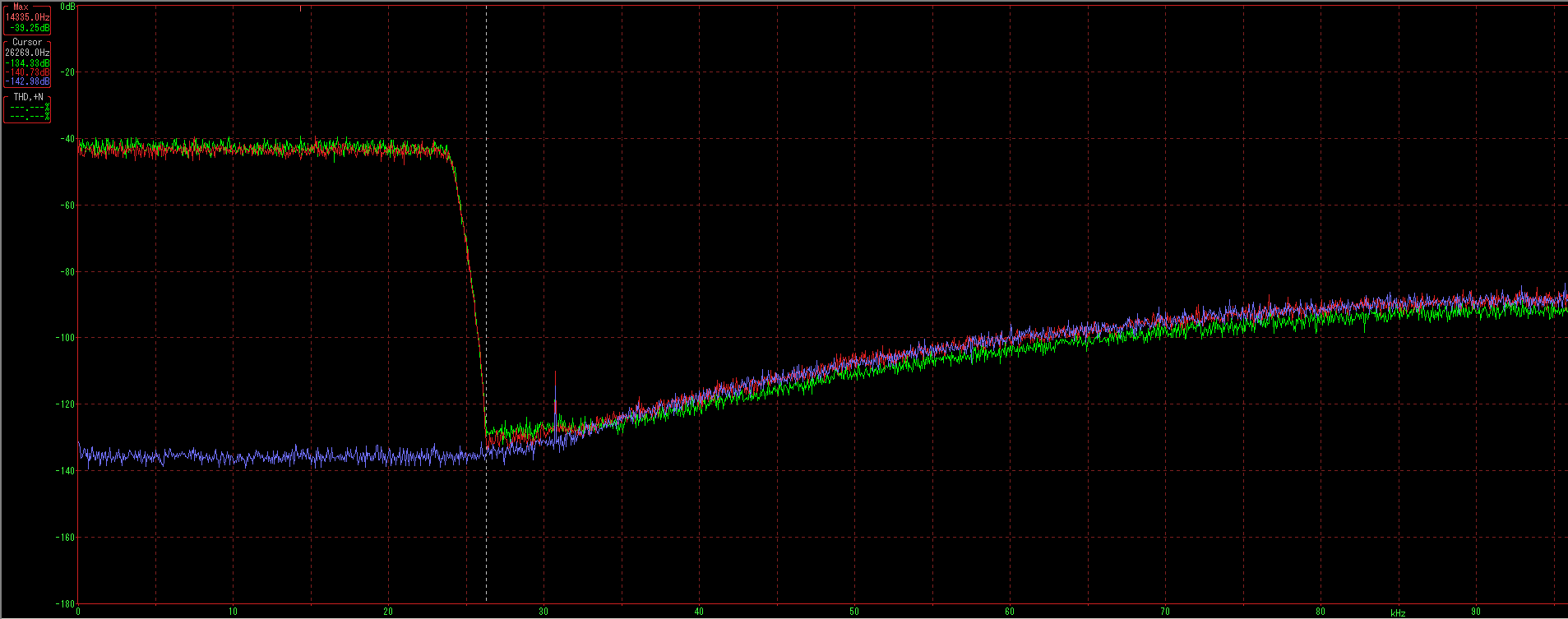
Here is a comparison of the Tact and the Focusrite 18i20 on the 0 dbFS noise signal. You can see the 18i20 interface has a bit steeper filter and the noise presumably from the sigma delta process starts at lower frequencies.
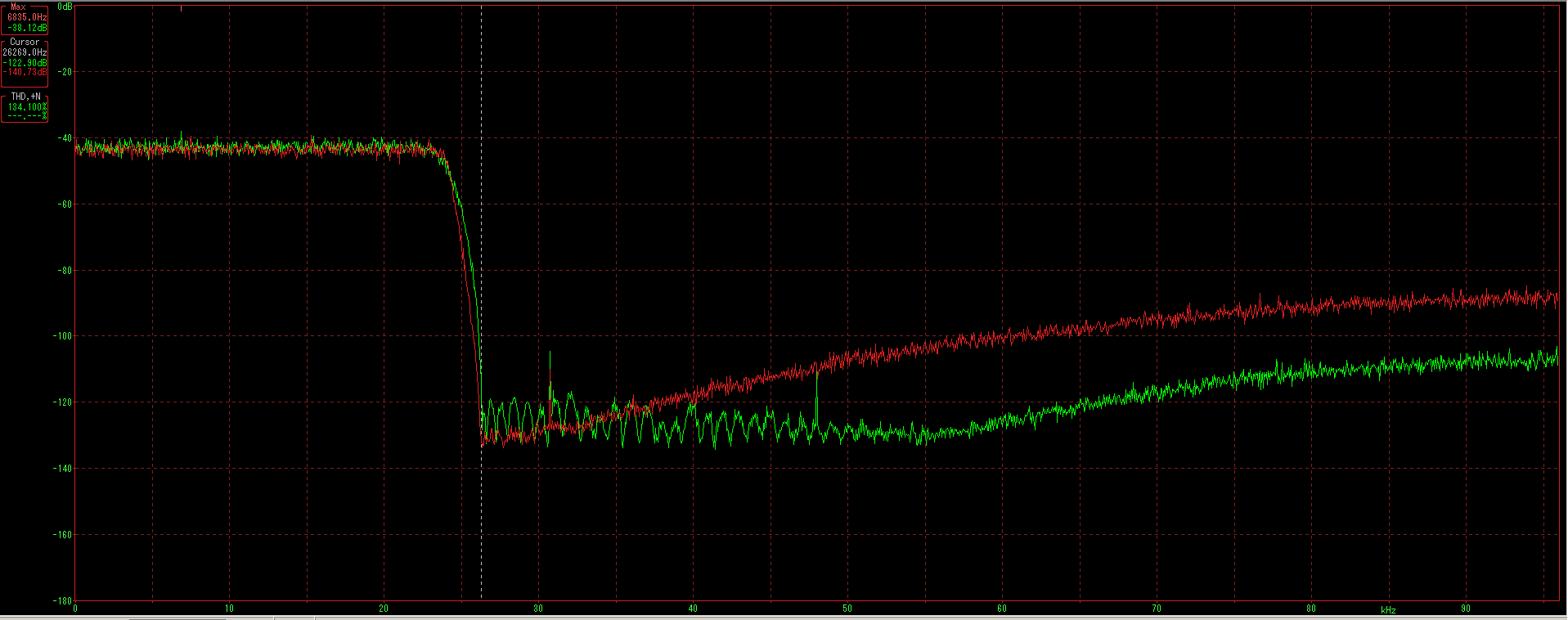
Next I used upsampling in the playback software to play the 48 khz file at 96 khz using the Focusrite 18i20. You see the ultrasonic noise level is elevated when software upsampled. Shown is 0 dbFS in red, -4 dbFS in green and -6 dbFS in blue. It appears by -6 db the effect is gone. This pretty well mirrors what upsampling in offline software was showing.
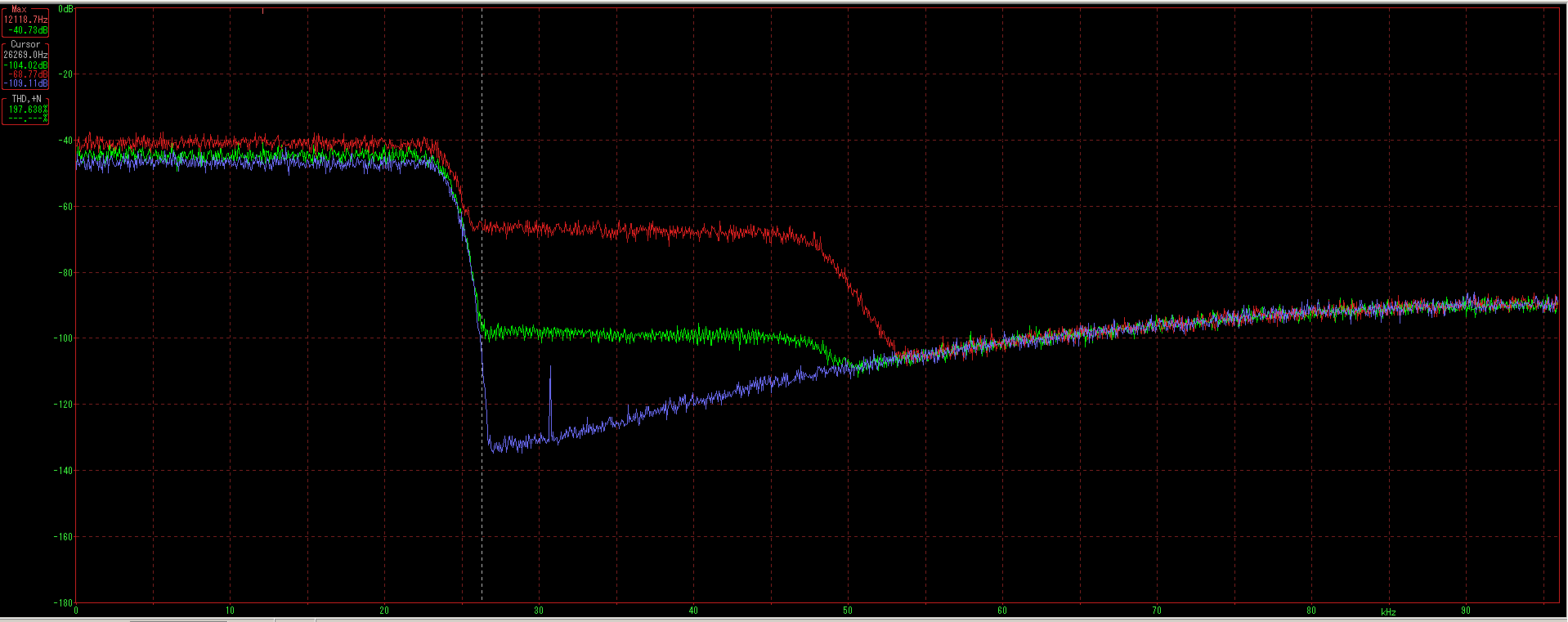
I also notice it this causes mirroring of the below 24 khz range at a lower level one more 24 khz band before rolling off. Is this why upsampling can sound different? The ultrasonic noise is not so far down in level as you get near 0 dbFS. I would think it can image back down into the below 20 khz band. Were it a transient, and no white noise existed there it could possibly be audible in level. Probably the level would be too low to be heard especially in the midst of other parts of the music. Nevertheless, it is one more good reason NOT to upsample your music upon playback. Instead best fidelity is likely at the native sample rate of the recording.
Ray was looking at a test signal I suggested for the Mytek Brooklyn review thread starting with the above post.
It is a test signal Juergen Reis of MBL suggested to JA of Stereophile. It is - 4dbFS of white noise played at a lower sample rate and measured at a much higher sample rate. The idea is the residual noise above nyquist of the original signal will reveal the shape/steepness of the anti-imaging filter on the DAC output.
Ray upsampled such a signal by 8x to better see the waveshape between samples as I had mentioned such a signal clipped an ADC at lower levels than a -.1 dbFS sine wave. Ray surmised these were intersample overs which seems reasonable. A question in my mind was whether such signals were showing us accurately the imaging filter shape or was it ultrasonic noise from the slight clipping. In upsampled signals the level of ultrasonic noise was higher if the original was -4 db FS than if it was -6 db FS by a pretty large amount. The ultrasonic noise was very high for a 0 dbFS white noise signal when upsampled. Now all of this was in software I should mention. Another question was whether upsampling playback software clipped such signals.
Some DACs have been known to have inadequate analog headroom for intersample overs and to have some clipping from that. I suspect that is why Reis chose - 4db as most well designed gear is not going to have an issue with a signal at that level in the analog output stage.
So I used an old Tact RCS 2.0 set unity gain to playback these signals at 48 khz, and recorded them at 192 khz with a Focusrite Forte. I should mention this is 93.9 on the Tact volume control as it applies digital gain above that level up to 99.9 settings. So this is no digital volume adjustment. I set input levels as high as possible on the Forte ADC as long as it did not indicate clipping. I had signals starting at 0 dbFS and going in 1 db steps to -7 dbFS.
To shorten the story, I found the intersample levels not to cause any clipping in the DAC done this way and the resulting FFT does appear to show the shape of the anti-imaging filter of the DAC. Also I found if I adjusted levels so that - 4db was also nearly, but not clipping the ADC input, the resulting noise profile was virtually identical to 0 db. Without resetting gain the shape of the response was the same at all levels other than being lower by 1 db each progression thru the test signal.
Here is the shape of the 0 dbFS noise signal in red, the gain adjusted - 4dbFS signal in green, and the silent noise floor in blue.
Here is the same comparison using a Focusrite 18i20 interface in place of the Tact.
Here is a comparison of the Tact and the Focusrite 18i20 on the 0 dbFS noise signal. You can see the 18i20 interface has a bit steeper filter and the noise presumably from the sigma delta process starts at lower frequencies.
Next I used upsampling in the playback software to play the 48 khz file at 96 khz using the Focusrite 18i20. You see the ultrasonic noise level is elevated when software upsampled. Shown is 0 dbFS in red, -4 dbFS in green and -6 dbFS in blue. It appears by -6 db the effect is gone. This pretty well mirrors what upsampling in offline software was showing.
I also notice it this causes mirroring of the below 24 khz range at a lower level one more 24 khz band before rolling off. Is this why upsampling can sound different? The ultrasonic noise is not so far down in level as you get near 0 dbFS. I would think it can image back down into the below 20 khz band. Were it a transient, and no white noise existed there it could possibly be audible in level. Probably the level would be too low to be heard especially in the midst of other parts of the music. Nevertheless, it is one more good reason NOT to upsample your music upon playback. Instead best fidelity is likely at the native sample rate of the recording.